Воздуходувная установка

Задание 10 Вариант 1

КУРСОВОЙ ПРОЕКТ

Расчетно-пояснительная записка

Дисциплина «Теория механизмов машин»

Студент __________/ Краснов.В.В /

Группа ТС-3619

Специальность «Автомобили и тракторостроение»

Руководитель __________________/ Крохмаль Н. Н. /

Комиссия __________________/_____________/

__________________/_____________/

Дата защиты _________

Оценка _________

Курган 2011

Содержание Стр.

Задание ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

Введение· ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

1 Геометрический синтез рычажного механизма∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

2 Кинематический анализ рычажного механизма∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

3 Динамический анализ основного рычажного механизма∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

4 Силовой анализ рычажного механизма∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

5 Проектирование эвольвентного зубчатого зацепления ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

6 Синтез планетарного механизма ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

7 Синтез кулачкового механизма ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

7.1 Проектирование закона движения толкателя ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

7.2 Определение размеров кулачкового механизма ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

Заключение ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

Литература ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

Приложения

Задание 10.

Воздуходувная установка.

Воздуходувная установка предназначена для создания воздушного потока. Ротор 5 установки приводится во вращение через планетарный механизм 4 двигателем внутреннего сгорания. Двигатель- двухтактный, одноцилиндровый, карбюраторный.

Основной механизм двигателя состоит из коленчатого вала (кривошипа) 1, шатуна 2 и поршня 3. Изменение давления газов на поршень представлено индикаторной диаграммой. Привод клапанов цилиндра осуществляется кулачковым механизмом. Кулачковый 6 и коленчатый 1 валы кинематически связаны между собой и вращаются с одной скоростью.

Запуск двигателя производится от электростартера 7 через зубчатую передачу 8,9. Маховик установлен на коленчатом валу 1.

Примечания: 1.Проектирование основного механизма провести по V_ср, n₁, l_AB/l_OB=4,0. Положение центра масс шатуна l_AS2=0,35 l_AB.

2. Спроектировать зубчатую передачу, составленную из колес 8 и 9, с модулем m=2,5 мм по условию отсутствия подрезания зубьев; планетарный механизм – по передаточному отношению.

3. Синтез кулачкового механизма провести по закону движения толкателя (рис. 1.а), ходу h_T толкателя и максимальному углу давления α_max=30⁰.

Исходные данные к заданию 10

Параметры	Обозначения	Единицы измерения	Вариант числовых значений
Средняя скорость поршня 3	Vср	м/с	12,0
Частота вращения коленчатого вала 1	n1	об/мин
Частота вращения ротора 5	n5	об/мин
Диаметр поршня 3	d	м	0,095
Максимальное давление в цилиндре	Pmax	МПа	4,0
Масса звеньев: m3=0,8 m2=0,05 m1	m3	кг	2,0
Моменты инерции звеньев: lS2=0,1 l01	lS2	кгм^2	0,030
Моменты инерции ротора 5 и планетарного механизма, приведенный к ротору 5	l5	кгм^2	0,015
Коэффициент неравномерности вращения коленчатого вала 1	δ	-	0,010
Число зубьев колес 8, 9	Z8	-
	Z9	-
Ход толкателя 10	hT	м	0,009
Фазовые углы поворота кулачка: φn=φ0=5 φв.в.	φn	град

ВВЕДЕНИЕ

Целью курсового проекта является проведение кинематического, динамического и силового анализа, а также синтез механизмов, входящих в состав одноцилиндрового двухтактного двигателя внутреннего сгорания.

Основным механизмом одноцилиндрового двухтактного двигателя внутреннего сгорания является кривошипно-шатунный механизм, преобразующий возвратно-поступательное движение поршня во вращательное движение коленчатого вала посредством шатуна.

Кинематический анализ механизмов заключается в исследовании движения звеньев механизмов независимо от сил, вызывающих это движение. В результате этого анализа определяются положения звеньев и траектории отдельных точек звеньев; линейные скорости отдельных точек и угловые скорости звеньев; линейные ускорения отдельных точек и угловые ускорения звеньев.

Задачи динамического анализа состоят в определении истинного закона движения звена приведения (коленчатого вала) и расчете маховика.

1 ГЕОМЕТРИЧЕСКИЙ СИНТЕЗ ОСНОВНОГО РЫЧАЖНОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1], на основании следующих исходных данных:

V_cр= 12,0 м/с – средняя скорость движения ползуна

n₁= 2200 об/мин – частота вращения кривошипа

λ= l_AB/l_OA= 4,0

k_AS2=0,35 – коэффициент задающий положение центра масс на шатуне

1.1 По известной средней скорости определяем ход ползуна

S= V_ср.×30 ÷ n=12,0×30 ÷2200=0,163 (м)

1.2 Зная ход ползуна определяем длину кривошипа

0,163÷2=0,0815 (м)

1.3 Зная длину кривошипа определяем длину шатуна

c = λ×l_OA = 0,0815×4,0=0,326 (м)

1.4 Определяем положение центра масс на шатуне

l_AS2=k_AS2×l_AB= 0,35×0,326=0,114 (м)

Вывод: В результате расчетов определены размеры звеньев кривошипно- ползунного механизма, эти данные будут использоваться в последующих разделах курсового проекта.

2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ ОСНОВНОГО РЫЧАЖНОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [2], на основании следующих исходных данных:

a=0,м- экстриситет кривошипно-ползунного механизма

l₁=0,0815,м- длинна кривошипа (l_ОА)

l₂=0,326,м- длина шатуна (l_АВ)

l_S2=0,114,м- отрезок задающий положение центра масс на шатуне (l_AS2)

φ=90⁰,град- угол задающий положение линии движения ползуна

n=360⁰,град- значение max угла поворота кривошипа за цикл движения механизма

2.1 Составим общую расчетную схему для φ

Для данной схемы выведем расчетное уравнение

Сумма векторов: l₁+ℓ₂=a+S, составим проекции векторов но оси координат:

x: ℓ₁×cosφ₁+ ℓ₂×cosφ₂=S

y: ℓ₁×sinφ₁+ ℓ₂×sinφ₂=a

sinφ₂=a- ℓ₁×sinφ₁÷ ℓ₂

√1-sin²φ₂=cosφ₂

S=ℓ₁×cosφ₁+ℓ₂×√1-(a - ℓ₁sinφ)² ÷ ℓ₂²

В результате решения системы уравнений получаем аналитическое выражение для расчета положения ползуна (точки В).

S_B=ℓ₁×cosφ₁+√ℓ₂² – (a-ℓ₁×sinφ₁)²

На основании полученной формулы выполним расчеты для 12 равностоящих положений кривошипа (шаг 30⁰), результаты расчетов занесем в таблицу 2.1:

Таблица 2.1 Значения перемещения ползуна

№полж.
SB, м	0,408	0,394	0,359	0,315	0,277	0,252	0,244	0,252	0,277	0,315	0,359	0,394	0,408

2.1 Рассчитаем угол положения шатуна для каждого расчетного положения, по формуле:

φ₂=arctg(a-ℓ₁×sinφ₁ ÷ S_B-ℓ₁×cosφ₁)

Результаты расчетов занесем в таблицу 2.2:

Таблица 2.2 Значение угла положения шатуна

№полж.
φ2, м		90.107	90.106	90.105	90.106	90.107	90.11	90.002	90.004	90.004	90.004	90.002

2.3 Рассчитаем аналог угловой скорости шатуна по формуле:

i₂₁=-ℓ₁×cosφ₁÷ℓ₂×cosφ₂

Результаты вычислений занесем в таблицу 2.3:

Таблица 2.3 Значение аналога угловой скорости шатуна

№полж.
i21	-0,25	-0,218	-0,128		0,128	0,218	0,25	0,218	0,128		-0,128	-0,218	-0,25

2.4 Рассчитаем аналог линейной скорости движения ползуна по формуле:

S_B^’=ℓ₁×(-sinφ₁)- ℓ₂₁×ℓ₂×sinφ₂

Результаты расчетов занесем в таблицу 2.4:

Таблица 2.4 Значения аналога линейной скорости движения ползуна

№полж.
SB^’, м		-0,05	-0,08	-0,082	-0,062	-0,032		0,032	0,062	0,082	0,08	0,05

2.5 Рассчитаем аналог углового ускорения в расчетных положениях по формуле:

i₂₁^’ =ℓ₁×sinφ₁+i₂₁²×ℓ₂×sinφ₂ ÷ ℓ₂×cosφ₂

Результаты расчетов занесем в таблицу 2.5:

Таблица 2.5 Значения аналога углового ускорения в расчетных положениях

№полж.
i21^’		0,12	0,218	0,258	0,218	0,12		-0,12	-0,218	-0,258	-0,218	-0,12

2.6 Рассчитаем аналог линейного ускорения ползуна по формуле:

S_B^’’=-ℓ₁×cosφ₁-i₂₁²×ℓ₂×cosφ₂- i₂₁^’ × l₂ × sinφ₂

Результаты расчетов занесем в таблицу 2.6:

Таблица 2.6 Значения аналога линейного ускорения ползуна

№полж.
SB^’’,м	-0,102	-0,081	-0,031	0,021	0,051	0,06	0,061	0,06	0,051	0,021	-0,031	-0,081	-0,102

Выполним кинематический анализ для центра масс шатуна.

2.7 Рассчитаем координаты центра масс (т.е точки S₂):

x_S2=ℓ₁×cosφ₁+ℓ_AS2×cosφ₂

y_S2=ℓ₁×sinφ₁+ℓ_AS2×sinφ₂

Результаты расчетов занесем в таблицу 2.7:

Таблица 2.7 Значения координат центра масс шатуна

№полож
xS2, м		-0,027	-0,046	-0,053	-0,046	-0,027		0,027	0,046	0,053	0,046	0,027
yS2, м	0,196	0,184	0,152	0,11	0,07	0,042	0,032	0,042	0,07	0,11	0,152	0,184	0,196

2.8 Определим проекции аналога скорости центра масс на координаты оси по формулам:

x_S2^’ =- ℓ₁×sinφ₁- i₂₁×ℓ_AS2×sinφ₂

y_S2^’ = ℓ₁×cosφ₁+ i₂₁×ℓ_AS2×cosφ₂

Результаты расчетов занесем в таблицу 2.8:

Таблица 2.8 Значения проекций аналога скорости центра масс на координаты оси

№полож
xS2^’, м	-0,053	-0,046	-0,027		0,027	0,046	0,053	0,046	0,027		-0,027	-0,046	-0,053
yS2^’, м		-0,044	-0,074	-0,082	-0,068	-0,038		0,038	0,068	0,082	0,074	0,044

2.9 Определим аналоги ускорения центра масс на координаты оси:

x_S2^’’= - ℓ₁×cosφ₁+ i₂₁^’×ℓ_AS2×sinφ₂- i₂₁²×ℓ_AS2×cosφ₂

y_S2^’’=ℓ₁×sinφ₁+ i₂₁^’ ×cosφ₂× ℓ_AS2- i₂₁²×ℓ_AS2×sinφ₂

Результаты расчетов занесем в таблицу 2.9:

Таблица 2.9 Значения аналогов ускорения центра масс на координатные оси

№полож
xS2^’’, м		0,027	0,046	0,053	0,046	0,027		-0,027	-0,046	-0,053	-0,046	-0,027
yS2^’’, м	-0,089	-0,075	-0,037	7,368*10^3	0,044	0,067	0,075	0,067	0,044	7,368* 10^-3	-0,037	-0,075	-0,089

Для наглядных представлений и проверки выполненных расчетов сделаем следующие графические построения:

2.10 Построим схему механизма для 12 равностоящих положениях в масштабе µ_ℓ.

µ_ℓ=ℓ_AB ÷ AB=0,326÷100=0,003 м/мм.

2.11 Построим планы скоростей механизма для 2-го и 8-го положения

Для этого составим уравнения:

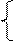V_B=V_A+V_BA

V_B=V_C4+V_BC4

V_A=ℓ_OA×ω₁=0,0815 (м).

µ_V=V_A÷(p_Va) =0,0815÷80=0,001

V_A=ω₁×ℓ_OA=1×0,0815=0,0815 (м/с).

2.12 Построим планы ускорений

Для этого составим уравнения:

a_B=a_A+ a_BA+ a^k_BA

a_B=a_C4+ a_BC4+ a^k_BC4

a_A=aⁿ_A+ a^τ_A

aⁿ_A=ω₁²× ℓ_OA=…

a^τ_A=ε₁×ℓ_OA=0

a_BA=aⁿ_BA+a^τ_BA

aⁿ_BA=ω₂²×ℓ_BA=…

ω₂=V_BA÷ ℓ_AB=…

a^τ_BA=ε₂×ℓ_BA=…

Результаты аналитического расчета отобразим графически.

2.13 Сравним результаты кинематического анализа выполненного двумя различными методами для контрольных положений 2 и 8.

	Графический метод	Аналитический метод
Положение 2	Положение 8
SB
SB′
SB′′
xS2
yS2
xS2′
yS2′
xS2′′
yS2′′

Сравнения результатов двух методов позволяет сделать вывод о правильности выполненных вычислений.

Вывод: В результате выполненных расчетов был проведен полный кинематический анализ кривошипно-ползунного механизма (2-мя методами).

Полученные результаты будут использованы при выполнении динамического и силового анализа механизма.

3 ДИНАМИЧЕСКИЙ АНАЛИЗ ОСНОВНОГО РЫЧАЖНОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [2] на основании следующих исходных данных:

P_max=P_max×(π×d_п.²)÷ 4=4× 3,14× 95²÷ 4=28338 Н –максимальное значение производственной силы;

где Р_max=4,0 МПа- максимальное давление в цилиндре;

d_п=95(мм) – диаметр поршня;

m₃=0,8 m₂=0,05 m₁- масса звеньев;

m₂=m₃÷0,8= 2÷ 0,8= 2,5(кг)- масса шатуна;

m₁=m₃÷0,05= 2÷0,05= 40(кг)-масса кривошипа;

m₃=2(кг)- масса ползуна;

J_S2=0,030(кгм²)-момент инерции относительно центра масс;

J_S2=0,1 J₀₁

J₀₁(J_S1)=0,3(кгм²);

J=(0,030+0,015)×(12500÷2200)²= 1,45

J=1,45- момент инерции вращающихся масс машины, приведенных к валу кривошипа;

δ=1÷100- коэффициент неравномерного вращения коленчатого вала;

n=360 –максимальный угол поворота кривошипа за один цикл;

ω_1ср= π×n₁ ÷30≈0,1×2200=220

Для упрощения динамического анализа составим динамическую модель кривошипно-ползунного механизма:

3.1 Выполним аппроксимацию производственной силы заданной графически в виде табличных данных изложенной в таблице 3.1:

Таблица 3.1 Значения производственной силы

№пол.
P, H	-8218	-2253	-15400	-9761,8	-7395,7	-5015,7	-3117,2	-1510,8		-771,9	-3152	-657,5

3.2 Составим расчетную формулу для определения приведенного момента сил.

М_пр=P_x×S_Bx′ + P_y×S_By′ +G₂×S_S2y′ +G₃×S_By′

где G₂=m₂×g=2,5×10=25;

G₃=m₃×g=2×10=20

Результаты расчетов занесем в таблицу 3.2:

Таблица 3.2 Значения приведенного момента сил

№пол
Мпр, Н/м		1,121× 10^3	1,23× 10^3	799,187	457,992	161,347	-3,116× 10^-14	-49,682	-2,861	-66,508	-254,329	-328,438	-1,101× 10^-15

Рассчитаем среднее значение момента:

М_пр.,ср=252,22

3.3 Выведем формулу для расчета приведенного момента инерции.

J_пр=m₃(S_Bx′ ² +S_By′ ²)+J_S2×i₂₁²+m₂(S_S2x′ ²+ S_S2y′ ²)+J₀₁

Результаты расчетов занесем в таблицу 3.3:

Таблица 3.3 Значения приведенного момента инерции

№пол.
Jпр.	0,308	0,31	0,32	0,329	0,32	0,31	0,3	0,31	0,32	0,329	0,32	0,31	0,308

3.4 Составим уравнение движения динамической модели в дифференциальной форме.

Уравнение движения решим численно, методом Баранова.

ω_i+1= М_пр.i×∆φ₁÷(J_пр.i+J)×ω_i + ((3×(J_пр.i+J)-J_пр.i+1-J)×ω_i ))÷ 2×(J_пр.i+J)

∆φ₁=1⁰=π÷180⁰

Результаты расчетов занесем в таблицу 3.4:

Таблица 3.4 Значения движения динамической модели в диф. форме

№пол.
ωi+1	-1,239	-1,539	-0,811	0,116	1,1712	1,8276	1,796	1,1967	0,280	-0,623	-1,075	-1,092	-1,228

ω_ср.=221,251

3.5 На основе расчета угловой скорости определим коэффициент неравномерности движения кривошипа.

δ=2×(ω_max-ω_min)÷ ω_max+ω_min=0,016 ω_max=223,143 ω_min=219,692

3.6 Для уменьшения коэффициента не равномерности δ, требуется установка маховика. Рассчитаем момент инерции маховика который обеспечит требуемую равномерность движения по формуле:

J_max=1÷(δ×ω_1ср.²) × ∑M_пр.i×∆φ₁ -(J_пр.max(1+δ)-J_пр.min(1-δ))÷2×δ=2,46

3.7 Решим снова уравнение движения динамической модели, но с учетом рассчитанного момента инерции маховика.

В результате расчета получим ω₁ указанной в таблице 3.7:

Таблица 3.7 Значения движения динамической модели с учетом рассчитанного момента инерции маховика

№пол.
ω1	-0,52	-0,645	-0,34	0,05	0,49	0,766	0,75	0,5	0,118	-0,26	-0,45	-0,458	-0,51

ω_{1 ср.}=220,524

3.8 На основании расчета ω определим новый коэффициент неравномерного движения δ.

δ_м=2×(ω_{i max}- ω_{i min} ÷ ǀω_{i max}+ ω_{i min}ǀ)=6,549×10^-3 ω_{i max}=221,316

ω_{i min}=219,871

3.9 Запишем формулу для обобщенного 2го закона Ньютона. По этой формуле определим значения углового ускорения динамической модели в расчетных положениях.

ε₁=М_пр.÷(J₀₁+J_пр.+J)-ω₁²÷(2×(J₀₁+J_пр. +J))×J_пр′;

где J_пр.i ′= (J_пр.i+1- J_пр.i) ÷∆φ₁

Результаты расчетов занесем в таблицу 3.9:

Таблица 3.9 Значения углового ускорения динамической модели

№пол.
ε	-58,7	58,35	133,102	175,081	150,942	47,213	-57,006	-135,7	-163,18	-121,03	-26,13	2,715	- 58,7

Вывод: В результате расчётов был определён закона движения плоского рычажного механизма. Эти данные будут использованы в последующих разделах курсового проекта.

4 СИЛОВОЙ АНАЛИЗ ОСНОВНОГО РЫЧАЖНОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [3], на основании следующих исходных данных:

ℓ₁=0,0818 м, - длинна кривошипа;

m₂=2,5 кг,- масса шатуна;

m₃=2 кг, - масса ползуна;

J_S2=0,030 – момент инерции 2-го звена;

J₀₁=0,3

n=360⁰- максимальный угол поворота кривошипа за один цикл;

γ=90⁰- угол задающий положения линии движения ползуна;

4.1 Составим расчетную схему для силового расчета механизма.

4.2 Определим в начале расчета силы инерции и моменты от силы инерции по формулам: Р_ин3=-m₃*a_B

P_ин2=-m₂*a_S2

M_ин2=-I_S2*ε₂

M_ин1=-I_A1*ε₁

результаты расчетов будут сохранены в базе данных компьютера и использоваться при последующих расчетах.

4.3 Составим уравнения статического равновесия для группы Ассура:

ü Cоставим уравнение равновесия М для звена 2 относительно В:

-R_1,2*l_AB-M_ин2+G₂*h_G2-P_ин2*h_Pин2=0

ü Составим уравнение равновесия сил для всей группы Ассура:

R_1,2+R_0,3+G₂+P_ин2+P_ин3+G₃+P₃+R_2,3=0

ü Cоставим уравнение равновесия сил для звена 3:

R_1,3+P_ин3+G₃+P₃+R_2,3=0

4.4 Решим составленное уравнение аналитически в проекциях на координатные оси в результате решения получим значения реакций во всех кинематических парах группы Ассура. Значения реакций занесем в таблицу 4.4:

№ пол.

R′12^T

1,48× 10^4

5,4× 10^3

9,96× 10^3

1,58× 10^4

2,07× 10^4

2,11× 10^4

1,97× 10^4

1,75× 10^4

1,33× 10^4

7,58× 10^3

6,48× 10^3

1,23× 10^4

2,3× 10^4

R′03^T

1,409

-654,

-1,34× 10^3

-2,28× 10^3

-2,57× 10^3

-1,38× 10^3

-1,376

918,

870,

-119,

-1,461× 10^3

-1,432× 10^3

1,409

R′23^T

4,09×10^3

1,28×10^4

1,18×10^4

1,25×10^4

1,39×10^4

1,25×10^4

1,06×10^4

8,9×10^3

6,25×10^3

3,32×10^3

1,56 ×10^3

3,53 ×10^3

1,23×10^3

Таблица 4.4 Значения реакций

4.5 Составим уравнения статического равновесия для входного звена:

R_2,1*h_P21+P_у*h_Pу-P₁*h_P1+M₁=0

R_0,1+P₁+P_у+R_2,1=0

4.6 Решим составленное уравнение аналитически в проекциях на координатные оси, результаты расчета занесем в таблицу 4.6:

Таблица 4.6 Значения совместных реакций

№ пол.
Rx01		- 3784,1	-7179,1	-	-	-	-	-	-	- 4211,5
Ry01	- 6,3788	-	- 6902,4	-	- 8188,3	- 46,30	6,1748	4170,7		6308,1		1775,1	- 6,378

4.7 Составим уравнения момента сил:

M_Ri=x_Ai × R_y21i - y_Ai × R_x21i

M_yi= -M_41i - M_Ri

Таблица 4.7 Момент сил

№ пол.
My′^T	- 247,	- 181,	- 230,	- 341,	- 377,	- 315,	- 240,	- 170,34	- 131,	- 164,	- 298,	- 361,	- 247,

Вывод: В результате расчётов были определены силы, действующие в кинематических парах механизма и уравновешивающие силы, уравновешенного момента, приложенные ко входному звену. Эти данные будут использованы в последующих разделах курсового проекта.

5 ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [4], на основании следующих исходных данных:

Число зубьев: шестерни z₈ =11;

колеса z₉ =21.

Модуль: m= 2,5 мм.

Угол наклона зубьев β= 0⁰

Стандартный угол профиля зубьев α=20⁰

Коэффициент высоты головки зуба h_a^*=1

Коэффициент радиального зазора с^*=0,25

Коэффициент смещения шестерни x₁=0,62;

колеса x₂= 0,28.

5.1 Определение межосевого расстояния а_w при заданных х₁, х_2.

х_∑ =0,9 – суммарный коэффициент смещения;

α_t × 180÷ π= 20 – угол профиля;

α_tw × 180÷ π= 26,339 – угол зацепления;

a_w= 41,942 – межосевое расстояние;

5.2 Определение диаметров зубчатых колес в (мм.):

d₁=27,5

d₂=52,5

u=1,909

d_w1=28,835 – начальный диаметр окружности колеса;

d_w2=55,049

a=40

y=0,777- коэффициент смещения;

∆y=x_∑ - y

∆y=0,123- коэффициент уравновешивающего смещения;

d_a1=34,984 – диаметр окружности вершин;

d_a2=58,284

d_f1= 24,35 – диаметр окружности впадин;

d_f2= 47,65

5.3 Проверка вычислений:

a_w= 41,942 – реальное межосевое расстояние;

a_w= 41,942

5.4 Расчет размеров для контроля взаимного положения разноименных профилей зубьев:

S_n1= 5,055 - толщина зубьев;

S_n2= 4,437

5.5 Расчет размеров для контроля номинальной поверхности зубьев:

d_b1= 25,842 – основная окружность;

d_b2= 49,334

α_а1 × 180÷ π= 42,382

α_а2 × 180÷ π= 32,174

p_p1= 3,091 – радиус кривизны;

p_p2= 6,818

5.6 Расчет размеров для контроля взаимного положения одноименных профилей зубьев:

р_b= 7,38

p_t= 7,854

p_x= -7,854×10¹⁰⁰

5.7 Проверка качества зацепления по геометрическим показателям:

x_1min= 0,357

x_2min= -0,228

p_L1= 4,228

p_L2= 8,078

ε_a= 1,179

S_na1= 0,906

S_na2= 1,857

S_b1= 5,136

S_b2= 4,904

S_w1= 4,71

S_w2= 3,525

5.8 Определение коэффициентов скольжения в зацеплении:

θ_p1= -1,629

θ_p2= -2,301

θ_a1= 0,224

θ_a2= 0,62

Вывод: При проектировании зубчатого эвольвентного зацепления были выбраны основные параметры, которые наилучшим образом удовлетворяют кинетическим, геометрическим, прочностным и экономичным требованиям.

6 СИНТЕЗ ПЛАНЕТАРНОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [4], на основании следующих исходных данных:

Тип механизма - плоский планетарный механизм с одинарными сателлитами (А), одним внешним и одним внутренним зацеплением.

i_1Н = 5,68 – передаточное отношение от звена 1 (солнечной шестерни) к водилу.

i_общ.= n_вх ÷ n_вых. = 12500÷ 2200 =5,68

i_kj= z_j ÷ z_k

i_общ.=i₁ ×i₂

Синтез планетарного механизма т.е определение чисел зубьев всех его зубчатых колес выполним на ПК с учетом следующих условий:

· обеспечение заданного передаточного отношения;

· условие соосности центральных звеньев механизма;

· условие соседства сателлитов (между сателлитами в механизме должен быть обеспечен зазор);

· условие сборки планетарного механизма (числа зубьев должны обеспечивать равномерное расположение сателлитов в механизме;

По результатам расчета выберем вариант обеспечивающий наименьшие габариты и массу планетарного механизма, построим кинематическую схему планетарного механизма в масштабе μ_z =0,5 зуб/мм., в двух проекциях.

k=4

z1=22

z2=40

z4=102

δi 1H =0

Вывод: В результате расчёта были рассчитаны числа зубьев колес, которые удовлетворяют условиям: сборки, соосности, соседства, правильного зацепления.

7 СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА

Расчеты в данном разделе будем выполнять по методике изложенной в [1] и [6], на основании следующих исходных данных:

Тип кулачкового механизма: плоский кулачковый механизм с вращающимся кулачком и поступательно движущимся толкателем.

Тип закона движения толкателя: параболический (а).

φ₁=35⁰ –угол подъема толкателя;

φ₂ = 7⁰ – угол верхнего выстоя;

φ₃ = 35⁰ – угол отпуска;

α_max= 30⁰ - максимальный допустимый угол давления;

h= 9 мм. – ход толкателя.

7.1 ПРОЕКТИРОВАНИЕ ЗАКОНА ДВИЖЕНИЯ ТОЛКАТЕЛЯ

В соответствии с заданным законом движения толкателя определим его перемещение, скорость и ускорение для 12-ти расчетных положений кулочка.

7.1.1 Рассчитаем перемещение толкателя в соответствии с формулами для заданного закона движения: S= h×(φ₂÷ φ_y×φ₁ ) при 0≤ φ ≤ φ₁

h ((1-φ_y÷φ_y – φ₁)×(1-φ÷φ_y)²) при φ₁≤ φ≤φ_y

результаты расчетов занесем в таблицу 7.1.1:

Таблица 7.1.1 Перемещение толкателя

№пол.
S (ψ)		0,54	2,16	4,86	7,92			7,92	4,86	2,16	0,54		-

7.1.2 Рассчитаем скорость толкателя в соответствии с формулами для заданного закона движения: S′= 2h (φ÷ φ_y –φ₁) при 0≤ φ ≤ φ₁

2h (1-φ÷φ_y)÷ (φ_y×φ₁) при φ₁≤ φ≤ φ_y

результаты расчетов занесем в таблицу 7.1.2:

Таблица 7.1.2 Скорость толкателя

№пол.
S^′ (ψ′)		8,839	17,68	26,52	17,68			-17,68	-26,52	-17,68	-8,839		-

7.1.3 Рассчитаем ускорение толкателя в соответствии с формулами для заданного закона движения: S′′= 2h (1÷ φ_y ×φ₁) при 0≤ φ ≤ φ₁

-2h (1÷φ_y × (φ_y- φ₁)) при φ₁≤ φ≤ φ_y

результаты расчетов занесём в таблицу 7.1.3:

Таблица 7.1.3 Ускорение толкателя

№пол.
S^′′ (ψ′′)	72,	72,	72,	72,	-144,71	-144,71	-144,171	-144,71	72,	72,	72,	72,	-

7.2 ОПРЕДЕЛЕНИЕ РАЗМЕРОВ КУЛАЧКОВОГО МЕХАНИЗМА

Плоский кулачковый механизм с поступательно движущимся толкателем.

7.2.1 Определим радиус основной окружности кулочка:

R₀= S′_max ÷ tgα_max -S_max÷ 2 = 48,931

e=0.

7.2.2 Определим координаты точек профиля кулочка в полярной системе координат по формулам:

R_i= r₀+S_i

β_i= φ_i ×180÷π

Результаты расчетов занесем в таблицу 7.2.2;

Таблица 7.2.2 Профиль кулочка в полярной системе координат

№ пол
Ri	48,93	49,47	52,4	55,7	56,91	56,93	56,59	53,98	50,46	48,97	---	---	--
βi												---	--

7.2.3 Для проверки правильности спроектированного механизма рассчитаем значение угла давления в расчетных положениях: α_i= arctg(S_i′ ÷ R₀ + S_i), результаты расчетов занесем в таблицу 7.2.3:

Таблица 7.2.3 Угол давления в расчетных положениях

№пол.
αi		15,058	30,03	20,429	1,093		-9,803	-28,63	-25,22	-2,85	---	---	- --

7.2.4 Определим допустимый радиус ролика:

r_p1=0,4× R₀ r_p1=19,573

r_p2=0,7×min(p_p) r_p2=8,605

7.3 В соответствии с результатами расчётов построим в масштабе следующие диаграммы: 1 Перемещение толкателя.

2 Аналога скорости толкателя.

3 Аналога ускорения толкателя.

4 Изменения угла давления.

5 Схема кулачкового механизма в масштабе μ_l=

Вывод: В результате расчётов были построены диаграммы перемещения, скорости, ускорения толкателя, а также диаграмма изменения угла давления. Построена кинематическая схема профиля кулачкового механизма.

Заключение

В результате проведения синтеза рычажного механизма определили размер

звеньев и вычертили кинематическую схему механизма.

В результате проведения кинематического анализа определили положения звеньев и траектории движения отдельных точек звеньев; линейные скорости отдельных точек и угловые скорости звеньев.

В результате проведенного динамического анализа определили:

-силы, приложенные к звеньям механизма;

-закон движения механизма под действием приложенной системы сил;

-выбирали необходимые конструктивные параметры механизма, обеспечивающие заданный режим движения механизма;

В результате проведения силового анализа выяснили неизвестные силы и моменты сил, приложенные к каждому звену исследуемого механизма, реакции в кинематических парах и уравновешивающую силу, приложенную ко входному звену

По исходным данным рассчитали основные геометрические параметры, размеры для контроля взаимного положения разноименных профилей зубьев, размеры для контроля номинальной поверхности зуба, размеры для контроля взаимного положения одноименных профилей зубьев, кинематические параметры проверили качество зацепления по геометрическим показателям. После чего построили картину рабочего зацепления и диаграмму удельных скольжений профилей зубьев.

Спроектировали профиль кулачка и определили его основные размеры.

Список литературы:

1. Артоболевский И.И., Теория механизмов и машин. – М.: Наука, 1975.

– 638с.

2. Геометрический синтез плоских рычажных механизмов. Методические указания. Составили: Крохмаль Н.Н. Курган: КМИ, 1995.- 17с.

3. Выполнение курсового проекта по теории механизмов и машин. Методические указания. Составили: Голофаст Л.М., Фонотов В.Т. Курган: КМИ, 1991. - 36с.

4. Силовой расчет механизмов. Методические указания. Составили: Голофаст Л.М., Фонотов В.Т. Курган: КМИ, 1992. - 38с.

5. Проектирование цилиндрической эвольвентной передачи с применением ПВМ. Методические указания. Составили: Голофаст Л.М., Фонотов В.Т. Курган: КМИ, 1993. - 22с.

Дата добавления: 2015-10-16