По индукции

Формулу включений-исключений можно доказать по индукции.

При формула включений-исключений тривиальна:

Пусть формула верна для , докажем ее для .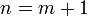

Пусть каждый элемент множества может обладать или не обладать любым из свойств . Применим формулу включений-исключений для свойств :

Теперь применим формулу для свойств к множеству объектов, для которых выполнено свойство :

Наконец, применим формулу для одного свойства к совокупности , объектов, которые не обладают свойствами :

Комбинируя выписанные три формулы, получим формулу включений-исключений для свойств . Что и требовалось доказать.

24. Линейной рекуррентной последовательностью (линейной рекуррентой) называется всякая числовая рекуррентная последовательность , задаваемая линейным рекуррентным соотношением:

с заданными начальными членами , где n — фиксированное натуральное число, — заданные числовые коэффициенты, . При этом число n называется порядком последовательности.

Чи́сла Фибона́ччи — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

в которой каждое последующее число равно сумме двух предыдущих чисел.

Более формально, последовательность чисел Фибоначчи 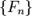задается линейным рекуррентным соотношением:

Дата добавления: 2015-10-13