Векторный

Каждая булева функция местности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2^n. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 2^2n

Таблица истинности — это таблица, описывающая логическую функцию.
Основные операции: ^, v, ->, <->, отрицание, сложение по модулю 2

16. Простой конъюнкцией или конъюнктом называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций.

Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.

Единичным вектором для данной функции называется тот вектор, значение

функции на котором равно 1.

Носителем данной функции – совокупность всех единичных векторов этой

функции (Nf – носитель функции f)

17.???

Булева функция g(x) называется импликантой булевой функции f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна единице.

Простой (первичной) импликантой булевой функции называется конъюнктивный терм, который сам является импликантой этой функции, но никакая его собственная часть уже не является импликантой этой функции.

18. Полином Жегалкина — полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:

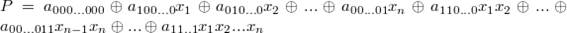
Построение полинома Жегалкина:

Пусть для функции 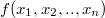задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.

19. Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции.

Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций 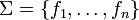. Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре Σ, который в данном случае называют также формулой.

20.

21. Прямое или декартовое произведение двух множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств.

Дата добавления: 2015-10-13