Транспортные задачи, задачи о назначениях.

Под задачей целочисленного программирования) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, если хотя бы одна зависимость — нелинейная, это будет целочисленная задача нелинейного программирования.

Особый интерес к задачам ЦП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. К их числу относятся:
• задачи оптимизации раскроя;
• оптимальное проектирование машин и оборудования;
• оптимизация системы сервиса и технического обслуживания машинно-тракторного парка и т.д.

Для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным.

Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программирования:

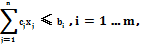
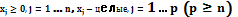
Если р = n, то задачу называют полностью целочисленной, если р < п — частично целочисленной.

Метод Гомори

Основан на понятии конгурентности действительных чисел любое действительное число можно представить в виде суммы целой и дробной части.

Х=[x]+{x}

[ ]- Целая часть

{ }-дробная часть

По методу Гомори первый этап решения целочисленных задач не отличается от обычного расчета по симплекс-методу. Если среди значений в оптимальном плане есть дробные, то составляется ограничение, отсекающее дробную часть, но оставляются в силе все прочие условия. Это дополнит.ограничение присоединяют к исходным и вновь применяется процедура симплекс метода.

Задача о назначениях— это распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.) и каждый ресурс может быть использован на одной и только одной работе. Исходные параметры задачи о назначениях

n— количество ресурсов;
m— количество работ;
a_i =1 — единичное количество ресурса A i=1…n (например: один работник, одно транспортное средство, одна научная тема и т.д.);
b_j=1— единичное количество работы B_j j=1..m (например: одна должность, один маршрут, одна лаборатория);
c_ij — характеристика качества выполнения работы B_J с помощью ресурса A_i (например: компетентность работника i при работе на должности j; время, за которое транспортное средство i перевезет груз по маршруту j; степень квалификации лаборатории i при работе над научной темой j).

Искомые параметры:
x_ij — факт назначения или неназначения ресурса A_i на работу B_j:

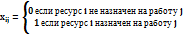
Экономико-математическая модель задачи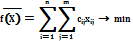

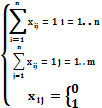
Экономико-математическая модель транспортной задачи Обозначим через x_ij количество единиц груза, запланированных к перевозке от поставщика i к потребителю j. Так как от поставщика i к потребителю j запланировано перевезти единиц груза x_ij, то стоимость перевозки составит c_ijx_ij

Транспортная задача относится к двухиндексным задачам линейного программирования, так как в результате решения задачи необходимо найти матрицу Xс компонентами x_ij.
Стоимость всего плана выразится двойной суммой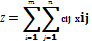

Систему ограничений получаем из следующих условий задачи:
а) все грузы должны быть перевезены, т.е. .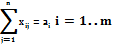

Таким образом, математическая модель транспортной задачи имеет следующий вид.

Найти минимальное значение линейной функции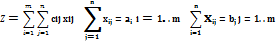

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

*)

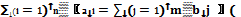Транспортная задача, в которой суммарные запасы и потреб­ности совпадают, т.е. выполняется условие *, называется закрытой моделью; в противном случае — открытой. Для открытой модели может быть два случая:

а) суммарные запасы превышают суммарные потребности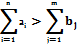

б) суммарные потребности превышают суммарные запасы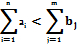

Открытая модель решается приведением к закрытой модели.
В случае «а», когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель B _n+1 потребность которого описывается формулой

а для случая «б», когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик A _m+1 запасы которого описываются формулой

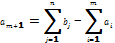
Стоимость перевозки единицы груза до фиктивного потребителя и стоимость перевозки груза от фиктивного поставщика полагаются равными нулю, так как груз в обоих случаях не перевозится.

МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА В данном методе запасы очередного по номеру поставщика используются для обеспечения запросов очередных по номеру потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.Заполнение таблицы транспортной задачи начинается с левого верхнего угла, поэтому и называется метод северо-западного угла.

Метод состоит из ряда однотипных шагов, на каждом из которых, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или один потребитель

МЕТОД МИНИМАЛЬНОЙ СТОИМОСТИ.Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(c_ij).

Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости:
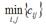и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.

Дата добавления: 2015-10-13