
|
Читайте также: |
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
Решение. В сумме 6 очков имеют следующие упорядоченные пары чисел: (1;5); (2;4); (3;3); (4;2); (5;1). Общее количество возможных исходов равно 36. Таким образом, 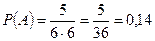 .
.
2. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Решение. В сумме 16 очков имеют следующие шесть упорядоченных троек чисел: (4;6;6); (6;4;6); (6;6;4); (6;5;5); (5;6;5); (5;5;6).Общее количество возможных исходов равно 216. Таким образом, 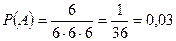 .
.
3. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение. Элементарное событие - спортсменка, выступающая первой. Всего 20 возможных исходов, 5 благоприятных.  .
.
4. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение. Всего 25 возможных исходов, из них 9 - благоприятных.  .
.
5. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Решение. Всего 80 исходов, благоприятных 18 – число выступлений, запланированных на третий день.  .
.
6. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение. Не подтекают 995 насосов из 1000, следовательно, вероятность того, что один случайно выбранный для контроля насос не подтекает, равна 0,995.
7. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение. Из каждых 108 сумок 100 не имеют дефектов. 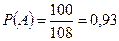 .
.
8. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение. Всего 25 исходов, из них 9 - благоприятных.  .
.
9. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение. Всего 25 исходов, из них 15 - благоприятных.  .
.
10. Монету бросают три раза. Найдите вероятность элементарного исхода ОРО.
Первое решение. Всего возможно 8 элементарных исходов: ООО, РОО, ОРО, ООР, ОРР, РОР, РРО, РРР. Таким образом, вероятность элементарного исхода ОРО равна 0,125.
Второе решение. Произошли три независимых события: при первом бросании выпал орел, при втором – решка, при третьем – орел. Вероятность каждого из них равна 0,5.
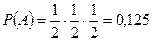
11. Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнет игру с мячом. Команда «Старт» играет по очереди с командами «Динамо», «Локомотив» и «Спартак». Найдите вероятность того, что «Старт» будет начинать только первую и третью игры.
Решение. Поскольку перед началом матча капитаны бросают монету, то условие задачи аналогично предыдущей. Также требуется найти вероятность исхода ОРО. Ответ: 0,125.
12. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно два раза.
Решение. Применим формулу Бернулли.  .
.
13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишень, а последние два раза промахнулся. Результат округлите до сотых.
Решение.  .
.
14. В классе 21 человек, среди них близнецы – Даша и Маша. Класс случайным образом делят на три группы по 7 человек в каждой. Найдите вероятность того, что Даша и Маша окажутся в разных группах.
Решение. Противоположное событие - Даша и Маша окажутся в одной группе (в первой, во второй или в третьей). Таким образом,  ;
; 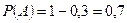 .
.
15. На фестивале органной музыки выступают 15 исполнителей, по одному от одной европейской страны. Порядок, в котором они выступают, определяется жребием, Какова вероятность того, что представитель Венгрии будет выступать после представителя Сербии, но перед музыкантом из Австрии?
Решение. Исполнители из трех указанных стран могут расположиться (не обязательно, подряд) шестью различными способами (число перестановок из трех). Благоприятствует данному условию только один из них. Ответ: 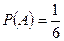 .
.
Замечание Ответ не зависит от общего числа исполнителей. Он определяется только числом участников, которых требуется расположить в заданном порядке.
16. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение. Определим события: А – кофе закончится в первом автомате; В – кофе закончится во втором автомате. По условию задачи,  и
и  (отметим, что эти события не являются независимыми, в противном случае
(отметим, что эти события не являются независимыми, в противном случае  ). По формуле вероятности суммы,
). По формуле вероятности суммы,  . Следовательно, вероятность противоположного события «кофе останется в обоих автоматах»
. Следовательно, вероятность противоположного события «кофе останется в обоих автоматах»  .
.
17. В банке три окна работы с клиентами. Вероятность того, что в случайный момент окно свободно, равна 0,3. Окна работают независимо друг от друга. В банк заходит клиент. Найдите вероятность того, что в этот момент свободно хотя бы одно окно.
Решение  .
.
18. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в пятницу в автобусе окажется меньше 30 пассажиров, равна 0,72. Вероятность того, что пассажиров окажется меньше 20, равна 0,35. Найдите вероятность того, что число пассажиров будет от 20 до 29.
Решение. Определим события: А - пассажиров будет меньше 20; В - пассажиров будет от 20 до 29; С - пассажиров будет меньше 30. Очевидно, что события А и В несовместны и  . Тогда
. Тогда  .
.  .
.
19. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение. Пусть 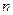 - искомое число выстрелов. Вероятность промаха при первом выстреле равна 0,6, при всех последующих – 0,4. Получим
- искомое число выстрелов. Вероятность промаха при первом выстреле равна 0,6, при всех последующих – 0,4. Получим



 ;
;
 ;
;  ;
;  ;
;  .
.
Ответ: 5 выстрелов
20. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение. Возможны две гипотезы:  - пациент болен;
- пациент болен;  - пациент здоров. По условию,
- пациент здоров. По условию,  ;
;  .
.
Событие  - анализ крови дал положительный результат. Тогда
- анализ крови дал положительный результат. Тогда  ;
;  . Согласно формуле полной вероятности,
. Согласно формуле полной вероятности,  , где
, где  . Следовательно,
. Следовательно,  .
.
Ответ: 0,0545.
Примечание: задача могла бы быть решена с помощью графов.
21. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение. Вероятность того, что 4 июля будет хорошая погода равна  , отличная -
, отличная -  .
.
Вероятность того, что 5 июля будет хорошая погода равна 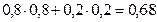 , отличная -
, отличная -  .
.
Вероятность того, что 6 июля будет хорошая погода равна  , отличная -
, отличная -  .
.
22. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение. Пусть  - доля продукции первого хозяйства в общем объёме закупок. Тогда получим уравнение
- доля продукции первого хозяйства в общем объёме закупок. Тогда получим уравнение  ;
; 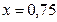 .
.
 .
.
23. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение. Возможны две гипотезы:  - револьвер пристреленный;
- револьвер пристреленный;  - не пристреленный. По условию,
- не пристреленный. По условию, 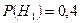 ;
;  . Событие
. Событие  - меткий выстрел. Тогда
- меткий выстрел. Тогда  ;
;  . Согласно формуле полной вероятности,
. Согласно формуле полной вероятности,  .
. 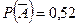 .
.
Ответ: 0,52.
24. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Решение.  .
.
Ответ: 0,0296.
25. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение. Событие  - абитуриент поступил на специальность «Лингвистика», событие
- абитуриент поступил на специальность «Лингвистика», событие  - абитуриент поступил на специальность «Коммерция», событие
- абитуриент поступил на специальность «Коммерция», событие 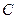 - абитуриент поступил хотя бы на одну из этих специальностей.
- абитуриент поступил хотя бы на одну из этих специальностей.  ,
,  .
. 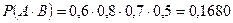 ,
,  .
.
Ответ: 0,408.
26. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
27. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу  .
.

28. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Дата добавления: 2015-10-13; просмотров: 341 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Translate into English. | | | Драгоценные истины 10 января |