
Читайте также:
|
Задание 1
Вычислить определенный интеграл по формуле Ньютона-Лейбница, а затем по формуле Симпсона, разбив интегральный отрезок на десять равных частей. Результаты вычислений округлять до четырех знаков после запятой.
Серия А:
1)  ; 2)
; 2) 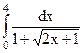 ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ;
;
8)  ; 9)
; 9)  ; 10)
; 10)  ;
;
Серия Б:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 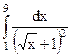 ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
Серия В:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6) 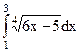 ; 7)
; 7)  ;
;
8)  ; 9)
; 9)  ; 10)
; 10) 
Задание 2
Серия А:
11. Вычислить площадь фигуры, ограниченной параболой
y = 4х-х2, осью абсцисс и прямой y = 1.
12. Вычислить площадь фигуры, ограниченную кривыми
y = lnx, y = e2x, х = 1, х = е.
13. Вычислить площадь фигуры, ограниченной кривой
y3 = х, и прямыми y =1 и х = 8.
14. Вычислить площадь фигуры, ограниченной кривой
y = tgx, осью ОХ и прямой х = π/3.
15. Вычислить площадь фигуры, ограниченной кривой
y = х3, прямой y = 8 и осью ОУ.
16. Вычислить площадь фигуры, ограниченной параболой
y = 2х - х2, и прямой y = -х.
17. Вычислить площадь фигуры, ограниченной параболами
y = х2,  и прямой y = 2х.
и прямой y = 2х.
18. Вычислить площадь фигуры, ограниченной параболами
 и
и  .
.
19. Вычислить площадь фигуры, ограниченной кривыми
y = ех, у = е-х и прямой х = 1.
20. Вычислить площадь фигуры, ограниченной параболами
y2 = 2рх и х2 = 2ру.
Серия Б:
11. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 6х + 5 и прямой y = х – 2.
12. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 5х + 6 и прямой y = х – 1.
13. Вычислить площадь фигуры, ограниченной кривой
y = х3 и прямой y = х.
14. Вычислить площадь фигуры, ограниченной параболами
y = х2 – х – 6 и y = 4х - х2.
15. Вычислить площадь фигуры, ограниченной параболами
y = х2 – 5х + 4 и y = 3х - х2.
16. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 5х + 4 и прямой y = 3 – х.
17. Вычислить площадь фигуры, ограниченной кривой y = cosx,
прямой y = 1/2 и осью ОХ.
18. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 8х + 15 и прямой y = 4 – х.
19. Вычислить площадь фигуры, ограниченной параболой
y = -х2 + 5х – 4 и прямой y = 3 – х.
20. Вычислить площадь фигуры, ограниченной параболами
y = 2х2 – 7х + 3 и y = -х2 +2х.
Серия В:
1. Вычислить площадь фигуры, ограниченной прямыми
y = 2х + 1, y = 4 – х и осью ОХ.
2. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 6х + 8 и прямой y = 15 – х.
3. Вычислить площадь фигуры, ограниченной прямыми
y = 3 – х, y = 4 + х и осью ОХ.
4. Вычислить площадь фигуры, ограниченной прямыми
 , y = 4х – 1 и осью ОУ.
, y = 4х – 1 и осью ОУ.
5. Вычислить площадь фигуры, ограниченной прямыми
 , y = - 3 – х и осью ОУ.
, y = - 3 – х и осью ОУ.
6. Вычислить площадь фигуры, ограниченной параболой
y = х2 – 2х – 3 и прямой y = 2 – х.
7. Вычислить площадь фигуры, ограниченной параболами
y = 3х2 – 10х + 3 и y = 2х – х2.
8. Вычислить площадь фигуры, ограниченной параболами
y = - 2х2 + х + 1 и y = (х – 1/2)2.
9. Вычислить площадь фигуры, ограниченной параболой
y = 2х2 + 7х + 3 и прямой y = ½ х +1.
10. Вычислить площадь фигуры, ограниченной кривой 
и прямыми y = 2 + х и х = 4.
 Задание 3
Задание 3
Провести необходимые вычисления, сделать чертёж.
Серия A.
1. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченной параболой  , прямой x=4 и осью OX.
, прямой x=4 и осью OX.
2. Вычислить площадь фигуры, ограниченной эллипсом x=2cost, y=3sint.
3. Найти объём тела, полученного вращением вокруг оси OY фигуры, ограниченной гиперболой  , осью OY и прямыми y=1, y=6.
, осью OY и прямыми y=1, y=6.
4. Вычислить площадь фигуры, ограниченной кривыми  и
и  .
.
5. Вычислить площадь фигуры, ограниченной астроидой  ,
,  .
.
6. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями  ,
, 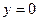 .
.
7. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченной параболами  и
и  .
.
8. Найти длину дуги кривой  от точки
от точки  1 до точки
1 до точки  12.
12.
9. Найти объём тела, образованного вращением вокруг оси OY фигуры, ограниченной линиями  ,
,  ,
, 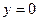 .
.
10. Найти длину одной арки циклоиды  .
.
Серия Б.
1. Вычислить площадь поверхности, образованной вращением вокруг оси OX параболы  от
от  1 до
1 до  7.
7.
2. Найти длину дуги полукубической параболы  от точки 0 (0;0), до точки М (4;8).
от точки 0 (0;0), до точки М (4;8).
3. Найти объём тела, полученного вращением вокруг оси OX фигуры, ограниченной гиперболой  и прямыми
и прямыми  0,
0,  1,
1,  4.
4.
4. Найти площади фигур, на которые парабола 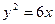 делит окружность
делит окружность  .
.
5. Найти площадь поверхности, образованной вращением вокруг оси OX астроиды  .
.
6. Найти площадь фигуры, ограниченной линиями  и
и  .
.
7. Вычислить объём тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями  ,
,  ,
,  0,
0,  .
.
8. Вычислить площадь фигуры, ограниченной линиями  и
и  .
.
9. Найти длину линии  от
от  до
до  .
.
10. Найти площадь поверхности, образованной вращением параболы  вокруг оси OX от вершины (0;0) до точки с абсциссой x=3a.
вокруг оси OX от вершины (0;0) до точки с абсциссой x=3a.
Серия В.
1. Найти объём тела, образованного при вращении вокруг оси Ох кривой  в промежутке
в промежутке  до
до  .
.
2. Найти объём тела, образованного вращением вокруг оси Ох площади, содержащейся между параболами  и
и  .
.
3. Найди длину дуги кривой  от
от  до
до  .
.
4. Найди длину дуги кривой  от
от  до
до  .
.
5. Вычислить площадь, заключённую между параболами  и
и  .
.
6. Вычислить площадь, заключённую между локоном Аньези  и параболой
и параболой
 .
.
7. Вычислить площадь двух частей, на которые круг  разделён параболой
разделён параболой  .
.
8. Вычислить площадь, ограниченную кривыми 
 и прямой х=1
и прямой х=1
9. Найти объём тела, образованного вращением площади, ограниченной полукубической параболой  , осью Ох и прямой х=1, вокруг оси Ох.
, осью Ох и прямой х=1, вокруг оси Ох.
10. Найти длину дуги логарифмической спирали  т>0.
т>0.
Дата добавления: 2015-09-06; просмотров: 252 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| По теме: Определенный интеграл, его приложения и приближенные вычисления | | | Глава про первую встречу |