Постановка задачи оптимального управления и критерии оптимальности.

Постановка задачи.

Необходимо найти алгоритм управления электромеханической системой описываемой дифференциальными уравнениями:

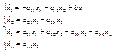
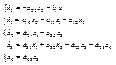
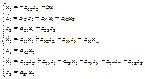
переводящий ее из начального состояния х₀ в конечное состояние х_к при минимизации критерия оптимальности и выполнении ограничений, накла­дываемых на систему:

Кроме того, могут быть дополнительные ограничения на производ­ную по току якорной цепи и момент упругого взаимодействия масс.

Критерии оптимальности могут быть различны: максимум быстро­действия, производительности; минимум нагрева, расхода энергии или топлива; максимум надежности; наилучшее качество и др. Всему ком­плексу этих требований, или комплексному критерию оптимальности, не может отвечать ни одна система, так как, во-первых, критерии взаимно исключают друг друга, во-вторых, если даже удастся вычислить ритм управления по этому комплексному критерию, то его технически невозможно будет реализовать.

Наиболее часто пользуются критериями оптимальности в виде ми­нимизации функционалов:

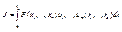
Дата добавления: 2015-09-05