
Читайте также:
|
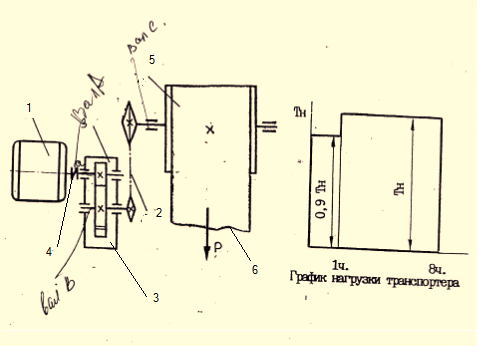
Рисунок 1 – Кинематическая схема
1 – электродвигатель;
2 – цепная передача;
3 – одноступенчатый цилиндрический косозубый редуктор;
4 – муфта упругая;
5 – приводной барабан;
6 – лента конвейерная
1.2 Выбор электродвигателя. Кинематический расчёт
Общий КПД привода ([МУ], с. 25)
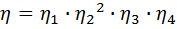 , (1)
, (1)
где  – КПД пары цилиндрических зубчатых колёс,
– КПД пары цилиндрических зубчатых колёс,  ;
;
 – КПД, учитывающий потери пары подшипников качения,
– КПД, учитывающий потери пары подшипников качения,  ;
;
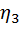 – КПД открытой цепной передачи,
– КПД открытой цепной передачи,  ;
;
 – КПД, учитывающий потери в опорах вала приводного барабана,
– КПД, учитывающий потери в опорах вала приводного барабана,  ;
;
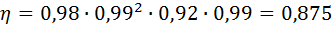 .
.
Мощность на валу барабана
 ; (2)
; (2)

Требуемая мощность электродвигателя
 ; (3)
; (3)
 .
.
Угловая скорость барабана
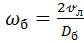 ; (4)
; (4)

Частота вращения барабана
 (5)
(5)
 .
.
В по требуемой мощности Ртр = 13,72кВт с учётом возможностей привода, состоящего из цилиндрического редуктора и цепной передачи, выбираем электродвигатель трёхфазный короткозамкнутый серии АО2, закрытый, обдуваемый, с синхронной частотой вращения 1500 об./мин АО2-64-4 У3, с параметрами
Рдв = 17 кВт и скольжением 5,1% (ГОСТ 19 523-81). Номинальная частота вращения п дв = 1500 – ((3,3/100)∙1500) = 1450,5 об./мин 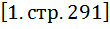 , а угловая скорость
, а угловая скорость
 (6)
(6)

Проверим общее передаточное отношение
 ; (7)
; (7)
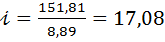 ,
,
что можно признать приемлемым, так как оно находится между 7 и 36 (большее значение принимать не рекомендуется).
Частные передаточные числа (они равны передаточным отношениям) можно принять для редуктора по ГОСТ 2185 – 66  для цепной передачи
для цепной передачи  .
.
Таблица 1 – Частоты вращения и угловые скорости валов редуктора и приводного барабана
| Вал А | 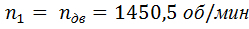
|  151,82 рад/с 151,82 рад/с
|
| Вал В | 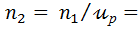 1450,5/5 = 290,1 об./мин 1450,5/5 = 290,1 об./мин
|  151,82/5
= 30,36 рад/с 151,82/5
= 30,36 рад/с
|
| Вал С |  84,93об./мин (см. выше) 84,93об./мин (см. выше)
| 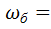 8,89 рад/с 8,89 рад/с
|
Вращающие моменты:
на валу шестерни
 (8)
(8)

на валу колеса
 (9)
(9)
 .
.
2 Расчёт зубчатых колёс редуктора
Материал шестерни – Сталь 50, улучшение, твердость 350 НB
Материал колеса – Сталь 50, улучшение, твердость 330 НB
Lh=3∙270∙2∙8=25920x
Эквивалентное число циклов перемены напряжений (6.33 ч.1[2])
- при расчете на контактную прочность
Для шестерни
 (10)
(10)
-для колеса
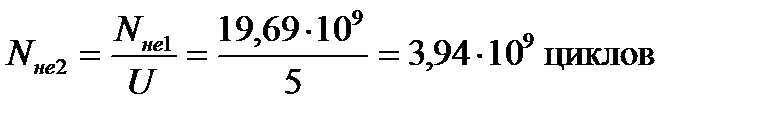 (11)
(11)
-при расчете на изгиб
- для шестерни

-для колеса
 (12)
(12)
где: с = 1 – число колес находящихся в зацеплении
Найдем коэф. долговечности (Zn и Yn)- при расчете на контактную прочность
- для шестерни
т.к. Nнe > Nнo
 (13)
(13)
где:Nно1 = 3.60 × 107 циклов – базовое число циклов перемены напряжений при твердости шестерни 350 HB (рис. 9.11[1])
- для колеса
т.к. Nнe < Nнo
 (14)
(14)
где:Nно2 = 3.16 × 107 циклов – базовое число циклов перемены напряжений при твердости колеса 330 HB (рис. 9.11[1])
– при изгибе
- для шестерни
 (15)
(15)
Принимаем Yn1 = 1
-для колеса

Принимаем Yn2 = 1
где: Nfo = 4.00 × 106 циклов – базовое число циклов (стр. 134 ч.1[2])
Определим допускаемые напряжения для шестерни и колеса
Предел контактной выносливости (табл. 9.8[1])
sн limb1=2 × HB + 70 = 2 × 350 + 70 = 770.00 МПа
sн limb2=2 × HB + 70 = 2 × 330 + 70 = 730.00 МПа
Допускаемые контактные напряжения (9.10 [1])


где: Sн = 1.1 – коэф. безопасности (прим. к 9.10 [1])
Для передач с прямым зубом принимают наименьшее
Предел выносливости на изгиб (табл. 9.8[1])
sf limb1= HB + 260 = 350 + 260 = 610.00 МПа
sf limb2= HB + 260 = 330 + 260 = 590.00 МПа
Допускаемые напряжения при изгибе (9.14 [1])


где: Sf = 1.70 – коэф. безопасности (прим. к 9.14[1])
Ya = 1.00 – коэф. приложения нагрузки (передача нереверсивная)
Yr = 1.20 – коэф. учитывающий шероховатость поверхности
Определяем межосевое расстояние.
Межосевое расстояние из условия контактной выносливости определяется по формуле
 , (16)
, (16)
где Ka– коэффициент для прямозубой передачи, Ka=49,5, [1, с. 32],
U – передаточное число редуктора,
Т– вращающий момент на ведомом валу,
КН – коэффициент, учитывающий неравномерность распределения
нагрузки, КН=1,15, [1, с.32];
[σH] – допускаемое контактное напряжение,
ψba – коэффициент ширины венца, ψba=0,3,
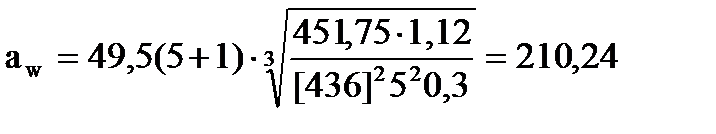 мм
мм
Принимаем  аω= 200мм
аω= 200мм
Определение модуля передачи.
 (17)
(17)
Принимаем стандартное значение по ГОСТ 2185 - 66: 
Определение чисел зубьев шестерни и колеса.
Z∑ =  , (18)
, (18)
где  – межосевое расстояние,
– межосевое расстояние,  =200 мм;
=200 мм;
m – нормальный модуль зацепления, m=4 мм.
Z∑ =  =10
=10
Принимаем Z∑=100.
Определяем числа зубьев шестерни и колеса.
Число зубьев шестерни равно:
 , (19)
, (19)
где Z∑= 100 – суммарное число зубьев.
Z1= 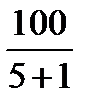 =16,67.
=16,67.
Принимаем Z1=17.
Определяем число зубьев колеса:
Z2= Z∑ -Z1, (20)
Z2=100-17=83.
Уточняем передаточное число

 (21)
(21)
где Z1 – число зубьев шестерни, Z1=17;
Z2 – число зубьев колеса, Z2=83.
U1ф=  4,9 (22)
4,9 (22)
Определение основных размеров шестерни и колеса.
Диаметры делительные:
 (23)
(23)

диаметры вершин
 (24)
(24)
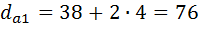 мм
мм
 мм
мм
Проверяем межосевое расстояние:
aw=  мм
мм
Ширина венца колеса:
 (25)
(25)

Примем b2=60 мм
Ширина венца шестерни 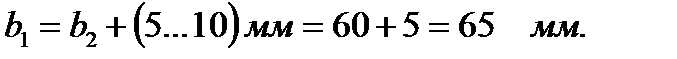
Коэффициент ширины шестерни по диаметру:
 (26)
(26)

Определяем окружные скорости и значения степени точности изготовления шестерни и колеса.
υ= 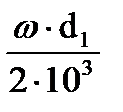 , (27)
, (27)
где  -угловая скорость шестерни
-угловая скорость шестерни
d1 – делительный диаметр шестерни.
υ =151,82⋅68/2⋅103=5,16м/с.
При данной скорости (до 10 м/с) принимаем 8 степень точности.
Определяем коэффициент нагрузки, проверяем зубья на контактное напряжение
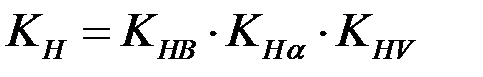 , (28)
, (28)
где KHB – коэффициент, учитывающий неравномерность
распределения нагрузки по ширине венца, KHB=1,03,[1, табл. 3.5];
KHα- коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями, KHα=1 -для прямозубых
[1, табл. 3.4];
KHV – динамический коэффициент, KHV=1,05 [1, табл. 3.6].
Кн=1,03∙1∙1,05=1,082.
Проверяем зубья на контактные напряжения:
 (29)
(29)
где aω – межосевое расстояние,
310-коэффициент для прямозубых колес.
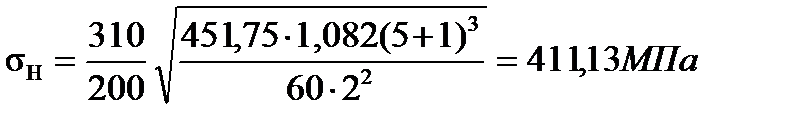
σH=411,13МПа<  =436МПа.
=436МПа.
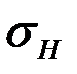 <
<  .
.
Определяем силы, действующие в зацеплении.
Определяем окружную силу:
Ft=  , (30)
, (30)
где Т– вращающий момент на валу шестерни,
d– делительный диаметр шестерни,
Ft=2∙90,35∙1000/68=2657H
 (31)
(31)

Проверяем зубья на выносливость по напряжениям изгиба
по формуле
 (32)
(32)
Здесь коэффициент нагрузки КF = КFB KFv(см. с. 42).
По табл. 3.7 при ψbd = 0.56, твердости НВ < 350 и симметричном расположении зубчатых колес относительно опор KFB = 1,065.
По табл. 3.8 KFv = 1,2.
Таким образом, коэффициент
KF = 1,065 ∙ 1,45 = 1,28;
YF — коэффициент, учитывающий форму
зуба и зависящий от эквивалентного числа зубьев


YF1 = 4,28 и Y F2 = 3,61
Допускаемое напряжение по формуле
 (33)
(33)
По табл. 3.9 для стали 45 улучшенной при твердости
НВ < 350  1.8НВ.
1.8НВ.
Для шестерни
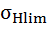 = 1,8∙350=630МПа;
= 1,8∙350=630МПа;
для колеса
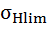 = 1,8 ∙ 330= 594 МПа
= 1,8 ∙ 330= 594 МПа
[SF] = [SF]' [SF]" - коэффициент безопасности [см. пояснения к формуле C.24)], где
[SF]' = 1,75 (по табл. 3.9), [SF]" = 1 (для поковок и штамповок). Следовательно, [SF] = 1,75.
Допускаемые напряжения:
для шестерни

для колеса

Находим отношения
 /YF
/YF
для шестерни
360/4,28=84,11
для колеса
339,43/3,61=94,02
Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.
Определяем коэффициенты YB и KFa
[см. гл. III, пояснения к формуле C.25)]:
для средних значений коэффициента торцового перекрытия
eа =1,5 и 8-й степени точности KF =0.92
Проверяем прочность зуба колеса по формуле
 (34)
(34)
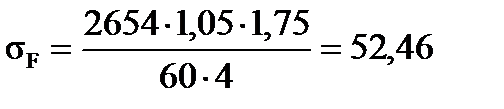

Условие прочности выполнено.
3 Предварительный расчёт валов редуктора
Валы предназначены для установки на них вращающихся деталей и передачи крутящего момента.
Конструкции валов в основном определяются деталями, которые на них размещаются, расположением и конструкцией подшипниковых узлов, видом уплотнений и техническими требованиями.
Валы воспринимают напряжения, которые меняются циклично от совместного действия кручения и изгиба. На первоначальном этапе проектирования вала известен только крутящий момент, а изгибающий момент не может быть определен, т.к. неизвестно расстояние между опорами и действующими силами. Поэтому при проектировочном расчете вала определяется его диаметр по напряжению кручения, а влияние изгиба учитывается понижением допускаемого напряжения кручения.
Дата добавления: 2015-10-13; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ДЕЙСТВИЕ ВТОРОЕ | | | Определение геометрических параметров ступеней валов |