
Читайте также:
|
§1. Решетки Бравэ кристаллов. Простая и сложные кристаллические решетки.
Кристаллы основная форма существования твердых тел около 95% литосферы занимают кристаллы.
С микроскопической точки зрения кристаллы представляют собой дискретную структуру, состоящую из огромного числа атомов или молекул образующих в пространстве правильную периодическую структуру. Свойства пространственной периодичности означает, что для каждого кристалла можно указать 3 некомпланарных вектора  таких что трансляция (параллельный перенос) кристалла на любой вектор
таких что трансляция (параллельный перенос) кристалла на любой вектор 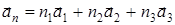 , где
, где  совмещает кристалл сам с собой все физически эквивалентные точки кристалла.
совмещает кристалл сам с собой все физически эквивалентные точки кристалла.  называются базисными (основными) векторами кристалла
называются базисными (основными) векторами кристалла  называются собственными векторами кристалла, они как видно представляют целочисленную комбинацию базисных векторов. Такие рассуждения верны только для кристаллов бесконечных размеров. При трансляции на вектор
называются собственными векторами кристалла, они как видно представляют целочисленную комбинацию базисных векторов. Такие рассуждения верны только для кристаллов бесконечных размеров. При трансляции на вектор  кристалла конечных размеров, края кристалла выходят за свои границы и, следовательно, кристалл не совмещается сам с собой. Мы также не учитываем тепловое колебание кристаллической решетки (адиабатическое приближение).
кристалла конечных размеров, края кристалла выходят за свои границы и, следовательно, кристалл не совмещается сам с собой. Мы также не учитываем тепловое колебание кристаллической решетки (адиабатическое приближение).
Будем откладывать из какой-нибудь точки кристалла вектор  , за начало отсчета лучше выбрать центр какого-либо атома, тогда концы векторов
, за начало отсчета лучше выбрать центр какого-либо атома, тогда концы векторов  образуют узлы (математическая абстракция). А совокупность узлов образует решетку Бравэ кристалла.
образуют узлы (математическая абстракция). А совокупность узлов образует решетку Бравэ кристалла.
 |
 называют элементарной ячейкой кристалла.
называют элементарной ячейкой кристалла.
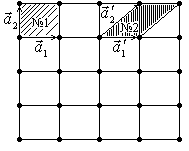 Выбор базисных векторов, а следовательно и элементарных ячеек не однозначен, это можно видеть на примере двухмерной плоской кристаллической решетки. Обычно кристаллы характеризуют такой элементарной ячейкой, которая обладает свойствами: 1) Они наилучшим образом отражают симметрию кристалла. 2) Чтобы у ячейки были прямые углы. 3) Имела наименьший объем
Выбор базисных векторов, а следовательно и элементарных ячеек не однозначен, это можно видеть на примере двухмерной плоской кристаллической решетки. Обычно кристаллы характеризуют такой элементарной ячейкой, которая обладает свойствами: 1) Они наилучшим образом отражают симметрию кристалла. 2) Чтобы у ячейки были прямые углы. 3) Имела наименьший объем 
 . Такая ячейка получила название примитивная ячейка. Для плоского кристалла ячейкой №1 можно характеризовать кристалл. Базисные вектора примитивных ячеек являются наименьшими в своих направлениях кристалла.
. Такая ячейка получила название примитивная ячейка. Для плоского кристалла ячейкой №1 можно характеризовать кристалл. Базисные вектора примитивных ячеек являются наименьшими в своих направлениях кристалла.
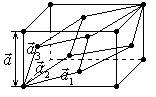 В разных кристаллах число атомов приходящихся на одну примитивную ячейку может быть разным. Кристаллы, у которых на одну примитивную ячейку приходится один атом (S=1), называют простой. Приведенная на рисунке плоская решетка является примером простой решетки. В ее примитивной ячейке атомы расположены только в вершинах. При этом каждый атом принадлежит своей ячейке ¼ частью, следовательно, на одну примитивную ячейку приходится 4·¼=1 атом. Примером кристалла с простой решеткой служит металл, кристаллы Cu, Ag, Ni, Au, Pb… Все они кристаллизуются в кубическую гранецентрированную решетку (кгр), т.е. кристаллы таких металлов можно получить повторением в пространстве куба, атомы находятся в вершинах и в центре шести боковых гранях. На гранецентрированный куб приходится 8·1/8 + 1/2·6 = 4 атома. На первый взгляд кажется, что металлы имеют сложную решетку, однако гранецентрированный куб у таких кристаллов не является примитивной. Примитивной ячейкой является ромбоэдрическая (куб вытянутый вдоль главной диагонали), ячейку можно построить на базисных векторах
В разных кристаллах число атомов приходящихся на одну примитивную ячейку может быть разным. Кристаллы, у которых на одну примитивную ячейку приходится один атом (S=1), называют простой. Приведенная на рисунке плоская решетка является примером простой решетки. В ее примитивной ячейке атомы расположены только в вершинах. При этом каждый атом принадлежит своей ячейке ¼ частью, следовательно, на одну примитивную ячейку приходится 4·¼=1 атом. Примером кристалла с простой решеткой служит металл, кристаллы Cu, Ag, Ni, Au, Pb… Все они кристаллизуются в кубическую гранецентрированную решетку (кгр), т.е. кристаллы таких металлов можно получить повторением в пространстве куба, атомы находятся в вершинах и в центре шести боковых гранях. На гранецентрированный куб приходится 8·1/8 + 1/2·6 = 4 атома. На первый взгляд кажется, что металлы имеют сложную решетку, однако гранецентрированный куб у таких кристаллов не является примитивной. Примитивной ячейкой является ромбоэдрическая (куб вытянутый вдоль главной диагонали), ячейку можно построить на базисных векторах  . В этой ячейки атомы расположены только в ее вершинах, значит, на нее приходится 1/8·8 =1 атом. Значит, перечисленные металлы имеют простую кристаллическую решетку. Кристаллы с простой решеткой состоят из атомов только одного типа. Структура решетки Бравэ у простых кристаллов совпадает со структурой кристаллической решетки. Некоторые кристаллы, состоящие из атомов одного типа (Ge, Si), а также все кристаллы состоящие из атомов разного типа имеют сложную кристаллическую решетку: у них на одну примитивную ячейку приходится более одного атома (S≥2). Для примера приведем сложную плоскую решетку, состоящую из атомов одного типа.
. В этой ячейки атомы расположены только в ее вершинах, значит, на нее приходится 1/8·8 =1 атом. Значит, перечисленные металлы имеют простую кристаллическую решетку. Кристаллы с простой решеткой состоят из атомов только одного типа. Структура решетки Бравэ у простых кристаллов совпадает со структурой кристаллической решетки. Некоторые кристаллы, состоящие из атомов одного типа (Ge, Si), а также все кристаллы состоящие из атомов разного типа имеют сложную кристаллическую решетку: у них на одну примитивную ячейку приходится более одного атома (S≥2). Для примера приведем сложную плоскую решетку, состоящую из атомов одного типа.
 Наименьшими базисными векторами в направлении х и у являются вектора
Наименьшими базисными векторами в направлении х и у являются вектора 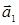 и
и 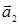 , модули которых занимают две клетки. Видно, что на примитивную ячейку приходится S = 4·1/4 + 1/2·4 = 3 атома. Значит, такой плоский кристалл, состоящий из атомов одного типа имеет сложную решетку (S = 3 атома).
, модули которых занимают две клетки. Видно, что на примитивную ячейку приходится S = 4·1/4 + 1/2·4 = 3 атома. Значит, такой плоский кристалл, состоящий из атомов одного типа имеет сложную решетку (S = 3 атома).
 На следующем рисунке приведен пример решетки, состоящей из атомов дух типов. Наименьшими собственными векторами такого кристалла в направлении осей х и у являются вектора
На следующем рисунке приведен пример решетки, состоящей из атомов дух типов. Наименьшими собственными векторами такого кристалла в направлении осей х и у являются вектора 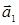 и
и  (наименьшие базисные вектора). Заштрихована примитивная ячейка кристалла, на нее приходится S = 1о + 1● = 2 атома. Такой кристалл имеет сложную решетку. Сложную решетку можно представить в виде системы простых решеток вдвинутых одна в другую определенным образом. Кристаллы характеризуются не только
(наименьшие базисные вектора). Заштрихована примитивная ячейка кристалла, на нее приходится S = 1о + 1● = 2 атома. Такой кристалл имеет сложную решетку. Сложную решетку можно представить в виде системы простых решеток вдвинутых одна в другую определенным образом. Кристаллы характеризуются не только  , но и векторами смещения
, но и векторами смещения  .
.
§2. Элементы симметрии кристаллов.
Миром кристаллов “правит” симметрия. Симметрия – это свойство тела или явления совпадать самим с собой (быть инвариантным). При определенных пространственных преобразованиях внешняя форма кристаллов, их симметрия являются результатом проявления симметрии расположения их атомов или молекул. Зная закон расположения атомов в кристалле, можно знать законы, по которым формируются грани и ребра внешней формы кристалла.
Помимо трансляционной симметрии, кристаллы характеризуются еще точечными преобразованиями симметрии. Это также преобразования, при которых остается неподвижной одна точка кристалла. К точечным преобразованиям относятся повороты вокруг осей, отражение в плоскостях и зеркальные повороты.
Точечные преобразования симметрии кристаллов удобно характеризовать с помощью элементов симметрии – это математические образы, относительно которых совершаются преобразования симметрии к элементам симметрии, плоскости симметрии и зеркально поворотные оси.
§2.1. Оси симметрии.
Ось симметрии это прямая, повороты вокруг которой совмещают кристалл сам с собой. Оси характеризуются своим порядком n. Порядок n это число совмещений кристалла при его повороте вокруг оси на 3600 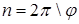 . φ – наименьший угол поворота, при котором кристалл совмещается сам с собой. Если кристалл совмещается при повороте на угол φ, то он будет совмещаться при последовательном m – кратном повторении операции поворота на угол φ. Если порядок оси n, то с ней связаны повороты на углы
. φ – наименьший угол поворота, при котором кристалл совмещается сам с собой. Если кристалл совмещается при повороте на угол φ, то он будет совмещаться при последовательном m – кратном повторении операции поворота на угол φ. Если порядок оси n, то с ней связаны повороты на углы  . Оси симметрии n-го порядка будем обозначать через Cn в отличие от поворотов
. Оси симметрии n-го порядка будем обозначать через Cn в отличие от поворотов  .
.  .
.
Примеры осей симметрии в кристаллах.
 Пример1: Бесконечная квадратная простая кристаллическая решетка имеет бесконечное число осей симметрии 4-го порядка. Все эти оси 4-го порядка эквивалентны, поэтому говорят, что он имеет одну ось симметрии 4-го порядка.
Пример1: Бесконечная квадратная простая кристаллическая решетка имеет бесконечное число осей симметрии 4-го порядка. Все эти оси 4-го порядка эквивалентны, поэтому говорят, что он имеет одну ось симметрии 4-го порядка.

Пример2: Кристаллы (NaCl) имеют три взаимно перпендикулярные оси 4-го порядка 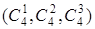 . На рисунке приведен фрагмент кристаллической решетки NaCl. Видно, что кристалл NaCl состоит из двух кубических гранецентрированных простых решеток, примитивная решетка ромбоэдрическая. На одну примитивную ячейку приходится 2 атома (один белый другой черный).
. На рисунке приведен фрагмент кристаллической решетки NaCl. Видно, что кристалл NaCl состоит из двух кубических гранецентрированных простых решеток, примитивная решетка ромбоэдрическая. На одну примитивную ячейку приходится 2 атома (один белый другой черный).
Докажем теорему, что кристаллы имеют оси симметрии только порядка n = 1, 2, 3, 4, 6 (кристаллы не могут иметь 5, 7 и более высоких порядков, это относится и к зеркально – поворотным осям симметрии).
Доказательство: представим себе, что кристаллы имеют ось симметрии малого порядка. С этой осью связаны повороты на углы:
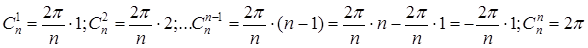
Видно, что вращения есть повороты на один и тот же угол в противоположных направлениях. Пусть ось Сn перпендикулярна плоскости рисунка и проходит через точку О, и пусть  наименьший собственный вектор кристалла перпендикулярной оси Сn.
наименьший собственный вектор кристалла перпендикулярной оси Сn.  являются преобразованиями симметрии кристаллов и следовательно они совмещают все эквивалентные точки кристалла, т.е. они переводят узлы решетки Бравэ в другие узлы этой же решетки. Переводят вектора
являются преобразованиями симметрии кристаллов и следовательно они совмещают все эквивалентные точки кристалла, т.е. они переводят узлы решетки Бравэ в другие узлы этой же решетки. Переводят вектора  в другие вектора этого же множества
в другие вектора этого же множества 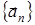 (
( - комбинация базисных векторов
- комбинация базисных векторов 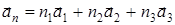 ).
).
Подействуем на вектор  преобразованиями и получим вектора:
преобразованиями и получим вектора:
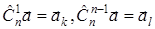 ,
,  ,
,  ;
;  ;
;
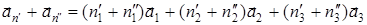 ;
;  ;
;  ,
,  (целое число), потому что
(целое число), потому что  наименьший собственный вектор в выбранном направлении
наименьший собственный вектор в выбранном направлении  ;
;  ;
;  ;
; 
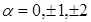
Подставляя найденные значения α в выражение 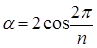 , находим что
, находим что  .
.
§2.2. Плоскости симметрии.
Плоскость симметрии – это такая плоскость, когда кристалл совмещается сам с собой, если все его точки одной части перенести за плоскость по перпендикуляру на равные расстояния.
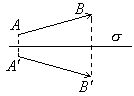 Подействуем преобразованием
Подействуем преобразованием  на вектор
на вектор  , получим:
, получим:  . Если плоскость σ перпендикулярна оси Сn, то плоскость обозначается σh, если плоскость σ проходит через ось Сn, то плоскость обозначается σv.
. Если плоскость σ перпендикулярна оси Сn, то плоскость обозначается σh, если плоскость σ проходит через ось Сn, то плоскость обозначается σv.
Теорема: Если кристаллы имеют оси симметрии порядка n≥3 (3,4,6), то они имеют и плоскости симметрии σv проходящие через эти оси.
 Доказательство: Докажем эту теорему только для оси
Доказательство: Докажем эту теорему только для оси  , с ней связаны повороты
, с ней связаны повороты 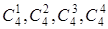 . Пусть
. Пусть 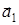 наименьший собственный вектор перпендикулярный оси С4. Подействуем на
наименьший собственный вектор перпендикулярный оси С4. Подействуем на 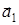 преобразованием
преобразованием  , получим:
, получим: 
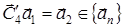 . Вектор
. Вектор  является наименьшим собственным вектором в своем направлении. Проведем через ось С4 и
является наименьшим собственным вектором в своем направлении. Проведем через ось С4 и 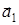 плоскость σv. Покажем, что эта плоскость будет являться плоскостью симметрии данного кристалла. Для этого надо знать, что любое преобразование α являлось преобразованием симметрии, если выполняется следующие условие:
плоскость σv. Покажем, что эта плоскость будет являться плоскостью симметрии данного кристалла. Для этого надо знать, что любое преобразование α являлось преобразованием симметрии, если выполняется следующие условие:
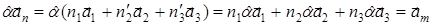 ;
;  ;
;  . Подействуем операцией σv на
. Подействуем операцией σv на 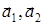 , получим:
, получим:
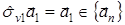 ;
;  ,
,  - третий базисный вектор кристалла. Введем вектор
- третий базисный вектор кристалла. Введем вектор 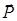 перпендикулярный оси С4,
перпендикулярный оси С4,  .
.
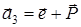 ,
,  ,
, 
 ,
,  плоскости в которой лежат вектора
плоскости в которой лежат вектора 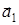 и
и  ;
;  ;
;  ;
;  ;
; 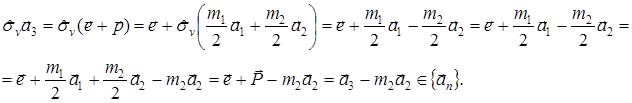
Следовательно, плоскость 
 , проходящая через оси симметрии четвертого порядка, является плоскостью симметрии кристалла. Например, кристаллы NaCl имеют три взаимно перпендикулярные плоскости симметрии, в которых, в соответствии с доказанной теоремой лежат оси симметрии четвертого порядка.
, проходящая через оси симметрии четвертого порядка, является плоскостью симметрии кристалла. Например, кристаллы NaCl имеют три взаимно перпендикулярные плоскости симметрии, в которых, в соответствии с доказанной теоремой лежат оси симметрии четвертого порядка.
§2.3. Зеркально – поворотные оси симметрии.
Зеркально – поворотная ось симметрии n – малого порядка (Sn) – это такая операция, при которой кристалл совмещается сам с собой, если произвести его поворот вокруг обычной оси n – малого порядка с последующем отражением кристалла в плоскости σh перпендикулярной оси n – го порядка. При этом в отдельности ни ось Cn ни плоскость σh не являются элементами симметрии кристалла, преобразованием симметрии является их комбинация (“произведение”), т.е. 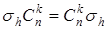 значит, зеркальный поворот
значит, зеркальный поворот 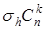 является самостоятельным элементом симметрии кристалла.
является самостоятельным элементом симметрии кристалла.
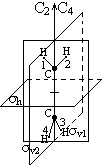 Для примера рассмотрим молекулу этилена C2H4, ее структура показана на рисунке. Атомы 1, 2 лежат в плоскости σv1, а 3, 4 в плоскости σv2. Эти плоскости пересекаются на линии С-С. Видно, что линия С-С является осью симметрии второго порядка С2. Плоскость σv1 является плоскостью симметрии молекулы, потому что, при отражении в ней атомы водорода 1 и 2, и атомы углерода остаются на месте, а атомы 3, 4 меняются местами, σv2 также является плоскостью симметрии. Ось С-С не является осью симметрии четвертого порядка (С4). Плоскость σh перпендикулярная оси С2 не является элементом симметрии молекулы, но видно что, если произвести поворот молекулы вокруг линии С-С на 900, а затем произвести отражение в плоскости σh, то молекула совпадет сама с собой. Следовательно, произведение
Для примера рассмотрим молекулу этилена C2H4, ее структура показана на рисунке. Атомы 1, 2 лежат в плоскости σv1, а 3, 4 в плоскости σv2. Эти плоскости пересекаются на линии С-С. Видно, что линия С-С является осью симметрии второго порядка С2. Плоскость σv1 является плоскостью симметрии молекулы, потому что, при отражении в ней атомы водорода 1 и 2, и атомы углерода остаются на месте, а атомы 3, 4 меняются местами, σv2 также является плоскостью симметрии. Ось С-С не является осью симметрии четвертого порядка (С4). Плоскость σh перпендикулярная оси С2 не является элементом симметрии молекулы, но видно что, если произвести поворот молекулы вокруг линии С-С на 900, а затем произвести отражение в плоскости σh, то молекула совпадет сама с собой. Следовательно, произведение  является самостоятельным преобразованием симметрии молекулу этилена значит, линия С-С является зеркально поворотной осью симметрии четвертого порядка:
является самостоятельным преобразованием симметрии молекулу этилена значит, линия С-С является зеркально поворотной осью симметрии четвертого порядка:  . Двукратно повторенная операция зеркального поворота также будет преобразованием симметрии:
. Двукратно повторенная операция зеркального поворота также будет преобразованием симметрии:  . Особым свойством обладает зеркальный поворот второго порядка S2, он называется инверсией:
. Особым свойством обладает зеркальный поворот второго порядка S2, он называется инверсией: 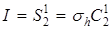 . Точка пересечения оси С2 с плоскостью σh называется точкой ин
. Точка пересечения оси С2 с плоскостью σh называется точкой ин  версии (центр симметрии).
версии (центр симметрии).  . Таким образом, операция инверсии переводит любой вектор
. Таким образом, операция инверсии переводит любой вектор  в
в 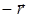 . Если кристалл имеет центр симметрии, то такой кристалл совмещается сам с собой, если все его точки перевести за цент по прямой на равные расстояния. Кристаллы NaCl имеют центр симметрии – точку О.
. Если кристалл имеет центр симметрии, то такой кристалл совмещается сам с собой, если все его точки перевести за цент по прямой на равные расстояния. Кристаллы NaCl имеют центр симметрии – точку О. 
 .
.
§3. Типы простых кристаллических решеток.
Структура простых кристаллических решеток совпадает со структурой своих решеток Бравэ. Сложные кристаллические решетки можно представить в виде системы S простых кристаллических решеток, сдвинутых одна относительно другой определенным образом. Используя три правила отбора, найдем все типы решеток Бравэ, т.е. все типы простых кристаллических решеток:
1. Кристаллы должны иметь оси n≥3 (3,4,6).
2. Кристаллы должны иметь плоскости симметрии σv.
3. Решетки Бравэ принадлежат трансляционному множеству  , в котором для каждого вектора
, в котором для каждого вектора  имеется ему обратный вектор
имеется ему обратный вектор  . А точечным преобразованием переводящим вектор
. А точечным преобразованием переводящим вектор  в вектор
в вектор  является операция инверсии, значит, любая решетка Бравэ имеет центр симметрии.
является операция инверсии, значит, любая решетка Бравэ имеет центр симметрии.
Существует всего 14 типов кристаллических решеток, распределенных по семи системам (сингониям): триклинная, моноклинная, ортогональная, тетрагональная, ромбоэдрическая, гексагональная, кубическая.
1.  Триклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами
Триклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми: 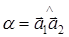 ;
;  ;
;  ;
;  , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
2. 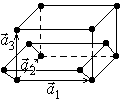
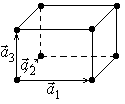 Моноклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами
Моноклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  ;
; 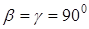 , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
3. Моноклинная базоцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  ;
; 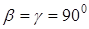 , и у которой атомы расположены в вершинах ячейки и в центре двух противоположных, прямоугольных гранях.
, и у которой атомы расположены в вершинах ячейки и в центре двух противоположных, прямоугольных гранях.
4. Ортогональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
5. Ортогональная базоцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах ячейки и в центре двух противоположных гранях.
, и у которой атомы расположены в вершинах ячейки и в центре двух противоположных гранях.
6.  Ортогональная гранецентрированная решетка, которую можно получить повторением в пространстве ячейки с ребрами
Ортогональная гранецентрированная решетка, которую можно получить повторением в пространстве ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах ячейки и в центрах всех шести гранях. Примитивной будет являться ячейка построенная на векторах
, и у которой атомы расположены в вершинах ячейки и в центрах всех шести гранях. Примитивной будет являться ячейка построенная на векторах  . Повторением такой решетки можно получить всю ортогональную гранецентрированную решетку.
. Повторением такой решетки можно получить всю ортогональную гранецентрированную решетку.
7.  Ортогональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами
Ортогональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах ячейки и в центре решетки.
, и у которой атомы расположены в вершинах ячейки и в центре решетки. 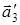 проеден к узлу в центре решетки. Примитивной будет являться ячейка построенная на векторах
проеден к узлу в центре решетки. Примитивной будет являться ячейка построенная на векторах  .
.
8. Тетрагональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 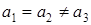 , углы между которыми:
, углы между которыми:  , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
9.  Тетрагональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами
Тетрагональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 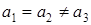 , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах и в центре ячейки. Центрирование граней ячеек не приведет к новому типу кристаллических решеток.
, и у которой атомы расположены в вершинах и в центре ячейки. Центрирование граней ячеек не приведет к новому типу кристаллических решеток.
10. Ромбоэдрическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
11.  Гексагональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами
Гексагональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 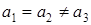 , углы между которыми:
, углы между которыми:  ;
; 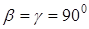 ,и у которой атомы расположены только в вершинах элементарной ячейки. Часто элементарные ячейки представляют в виде шестигранной призмы, которая состоит из трех четырехгранных призм, в частности ось симметрии шестого порядка.
,и у которой атомы расположены только в вершинах элементарной ячейки. Часто элементарные ячейки представляют в виде шестигранной призмы, которая состоит из трех четырехгранных призм, в частности ось симметрии шестого порядка.
12. Кубическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены только в вершинах элементарной ячейки.
, и у которой атомы расположены только в вершинах элементарной ячейки.
13. Кубическая гранецентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах и в центрах всех шести гранях ячейки. Примитивная ячейка – ромбоэдрическая.
, и у которой атомы расположены в вершинах и в центрах всех шести гранях ячейки. Примитивная ячейка – ромбоэдрическая.
14. Кубическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами  , углы между которыми:
, углы между которыми:  , и у которой атомы расположены в вершинах и в центре ячейки.
, и у которой атомы расположены в вершинах и в центре ячейки.
Кристаллические структуры сложных кристаллов состоят из систем одной из 14-ти типов простых решеток.
§4. Кристаллографические индексы Миллера.
 Для обозначения плоскостей и направлений кристалла используются так называемые кристаллографические индексы Миллера. Для их получения проведем оси координат X,Y,Z вдоль базисных векторов
Для обозначения плоскостей и направлений кристалла используются так называемые кристаллографические индексы Миллера. Для их получения проведем оси координат X,Y,Z вдоль базисных векторов 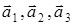 . Пусть некоторая плоскость пересекает такую координатную систему в точках с координатами:
. Пусть некоторая плоскость пересекает такую координатную систему в точках с координатами:  ;
;  ;
;  .
. 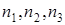 - целые или дробные числа, выражают наклон плоскостей по отношению к осям координатной системы. Теперь составим отношение обратных чисел
- целые или дробные числа, выражают наклон плоскостей по отношению к осям координатной системы. Теперь составим отношение обратных чисел 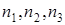 и приведем это отношение к отношению наименьших целых чисел:
и приведем это отношение к отношению наименьших целых чисел:  ; R - наименьшее кратное, а h, k, l и есть индексы Миллера для указанной плоскости. При обозначении плоскостей индексы Миллера заключаются в круглые скобки, без каких либо знаков между ними.
; R - наименьшее кратное, а h, k, l и есть индексы Миллера для указанной плоскости. При обозначении плоскостей индексы Миллера заключаются в круглые скобки, без каких либо знаков между ними.
Предположим  ;
;  ;
;  . Такие же индексы будут иметь остальные плоскости параллельные ей. Если плоскость параллельна одной из координатных осей, то соответствующий индекс равен нулю, если плоскость отсекает координату при отрицательных значениях, то над соответствующим индексом Миллера сверху ставится знак “-”. Направления перпендикулярные плоскости (hkl) обозначаются теми же индексами заключенными в квадратные скобки [hkl]. Система плоскостей одного кристаллографического типа обозначаются {hkl}, направления обозначаются <hkl>. Для примера найдем обозначения характерных плоскостей и направлений в кристаллах кубической системы (а1 = а2 = а3 = а; α = β= γ= 900). Для этого вырежем кристалл в форме куба с ребрами вдоль базисных векторов
. Такие же индексы будут иметь остальные плоскости параллельные ей. Если плоскость параллельна одной из координатных осей, то соответствующий индекс равен нулю, если плоскость отсекает координату при отрицательных значениях, то над соответствующим индексом Миллера сверху ставится знак “-”. Направления перпендикулярные плоскости (hkl) обозначаются теми же индексами заключенными в квадратные скобки [hkl]. Система плоскостей одного кристаллографического типа обозначаются {hkl}, направления обозначаются <hkl>. Для примера найдем обозначения характерных плоскостей и направлений в кристаллах кубической системы (а1 = а2 = а3 = а; α = β= γ= 900). Для этого вырежем кристалл в форме куба с ребрами вдоль базисных векторов  . Оси x,,y, z
. Оси x,,y, z  направлены вдоль базисных векторов. Найдем индексы Миллера для заштрихованной плоскости 1. Она пересекает координатные оси в точках с координатами:
направлены вдоль базисных векторов. Найдем индексы Миллера для заштрихованной плоскости 1. Она пересекает координатные оси в точках с координатами:  ;
;  ;
;  . Тогда индексы Миллера для плоскости 2: (010), для 3: (001). x1[100], y1[010], z1[001]. Плоскость противоположную (100), обозначают
. Тогда индексы Миллера для плоскости 2: (010), для 3: (001). x1[100], y1[010], z1[001]. Плоскость противоположную (100), обозначают  и так
и так
 |
 |
 ,
,  ,
,  кристаллографически одинаковые и их обозначают {100}. На рисунке заштрихована плоскость (110), для этой плоскости одинаковыми являются плоскости (011), (101). На следующем рисунке заштрихована плоскость (111). Для обозначения плоскостей в кристаллах гексагональной системы используют 4 индекса Миллера, для этого проводят че
кристаллографически одинаковые и их обозначают {100}. На рисунке заштрихована плоскость (110), для этой плоскости одинаковыми являются плоскости (011), (101). На следующем рисунке заштрихована плоскость (111). Для обозначения плоскостей в кристаллах гексагональной системы используют 4 индекса Миллера, для этого проводят че  тыре координатные оси x, y, u, z,. Ось z параллельна ребру а3.
тыре координатные оси x, y, u, z,. Ось z параллельна ребру а3.  ;
;  .
.
Плоскость перпендикулярная оси  называется базисной плоскостью. Оси x, y, u располагают в базисной плоскости под углом 1200 друг к другу. Для тог чтобы найти (hkil), находят координаты точек пересечения с кристаллографическими осями.
называется базисной плоскостью. Оси x, y, u располагают в базисной плоскости под углом 1200 друг к другу. Для тог чтобы найти (hkil), находят координаты точек пересечения с кристаллографическими осями.
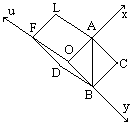 Для примера найдем индексы Миллера для плоскости АВ, которая перпендикулярна плоскости рисунка. Координаты точек пересечения этой плоскостью координатных осей:
Для примера найдем индексы Миллера для плоскости АВ, которая перпендикулярна плоскости рисунка. Координаты точек пересечения этой плоскостью координатных осей:  ,
, 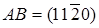 ;
;  ;
;  . Следовательно, направления вдоль оси z есть [0001], i = - (h+k). Возникает вопрос, почему используем четыре а не три индекса Миллера при обозначении плоскостей и направлений в кристаллах гексагональной системы. Оказывается, что при обозначении тремя индексами Миллера однотипные плоскости кристаллов гексагональной системы имели бы разное число единиц и нулей, и их нельзя было бы обозначить как {hkl}. Для примера уберем ось u, тогда плоскости СВ=(010),
. Следовательно, направления вдоль оси z есть [0001], i = - (h+k). Возникает вопрос, почему используем четыре а не три индекса Миллера при обозначении плоскостей и направлений в кристаллах гексагональной системы. Оказывается, что при обозначении тремя индексами Миллера однотипные плоскости кристаллов гексагональной системы имели бы разное число единиц и нулей, и их нельзя было бы обозначить как {hkl}. Для примера уберем ось u, тогда плоскости СВ=(010),  ,
, 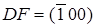 . Обозначение этих плоскостей имеют вид:
. Обозначение этих плоскостей имеют вид:  ,
,  , видно что все однотипные плоскости CB, DB, DF, FL имеют две единицы и два нуля, и тогда их можно обозначить {1100}.
, видно что все однотипные плоскости CB, DB, DF, FL имеют две единицы и два нуля, и тогда их можно обозначить {1100}.
§5. Обратная решетка кристалла и ее ячейка Вигнерра – Зейтца. Зоны Бриллюэна кристалла.
Для каждой прямой решетки кристалла можно построить ей обратную. Обратные решетки широко используются в зонной теории твердых тел при описании движения электронов проводимости и фотонов. Пусть прямая решетки кристалла характеризуется базисными векторами  и собственными векторами
и собственными векторами 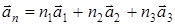 . Обозначим через
. Обозначим через  базисные вектора обратной решетки кристалла. Свяжем базисные вектора прямой и обратной решетки кристалла условием, что скалярное произведение:
базисные вектора обратной решетки кристалла. Свяжем базисные вектора прямой и обратной решетки кристалла условием, что скалярное произведение:
 ;
;  (1)
(1)
Условию (1) удовлетворяет следующие вектора:
 ;
;
 ; (2)
; (2)
 .
.
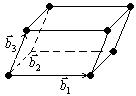
 Видно что,
Видно что, 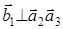 ,
,  ,
,  , значит
, значит  ,
,  , также
, также 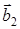 и
и  , т.е.
, т.е.  перпендикулярна двум базисным векторам прямой решетки, индексы которых отличаются от j. Видно, что тройка векторов
перпендикулярна двум базисным векторам прямой решетки, индексы которых отличаются от j. Видно, что тройка векторов 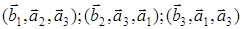 образуют правовинтовые системы, если
образуют правовинтовые системы, если 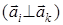 и
и  . На основе векторов
. На основе векторов  построим бесконечную совокупность векторов
построим бесконечную совокупность векторов 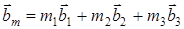 (3); где
(3); где  , т.е.
, т.е.  представляют собой целочисленную комбинацию векторов
представляют собой целочисленную комбинацию векторов  , они имеют размерность что и базисные вектора, а базисные вектора имеют размерность обратную длине, иными словами
, они имеют размерность что и базисные вектора, а базисные вектора имеют размерность обратную длине, иными словами  лежат в обратном пространстве. Будем откладывать с какой-нибудь точки - вектора
лежат в обратном пространстве. Будем откладывать с какой-нибудь точки - вектора  Концы таких векторов образуют узлы обратной решетки, а совокупность узлов есть обратная решетка кристалла. Если
Концы таких векторов образуют узлы обратной решетки, а совокупность узлов есть обратная решетка кристалла. Если  назывались собственными векторами прямой решетки, то
назывались собственными векторами прямой решетки, то  являются собственными векторами обратной решетки. Ячейка построенная на базисных векторах
являются собственными векторами обратной решетки. Ячейка построенная на базисных векторах  называется элементарной ячейкой обратной решетки, ее объем равен
называется элементарной ячейкой обратной решетки, ее объем равен  .
.
Бесконечным повторением в обратном пространстве элементарной ячейки можно получить всю бесконечную обратную решетку. На одну элементарную ячейку приходится один узел, следовательно число ячеек образующих обратную решетку равно числу ее узлов.  ;
;  . Элементарную ячейку обратной решетки можно получить иначе. Для этого возьмем какой-нибудь узел (Г) обратной решетки за начало отсчета. Проведем из этого узла (Г) прямые линии в ближайшие соседние узлы через середины этих перпендикулярно к ним проведем плоскости. Многогранник, полученный в результате пересечения плоскостей называется ячейкой Вигнера-Зейца. Возле каждого узла обратной решетки можно построить такую ячейку, при этом исходя из условия построения ячейки Вигнера-Зейца они не будут пересекаться и заполнят весь объем обратного пространства. Следовательно, объем ячейки Вигнера-Зейца равен объему параллелепипеда построенного на векторах
. Элементарную ячейку обратной решетки можно получить иначе. Для этого возьмем какой-нибудь узел (Г) обратной решетки за начало отсчета. Проведем из этого узла (Г) прямые линии в ближайшие соседние узлы через середины этих перпендикулярно к ним проведем плоскости. Многогранник, полученный в результате пересечения плоскостей называется ячейкой Вигнера-Зейца. Возле каждого узла обратной решетки можно построить такую ячейку, при этом исходя из условия построения ячейки Вигнера-Зейца они не будут пересекаться и заполнят весь объем обратного пространства. Следовательно, объем ячейки Вигнера-Зейца равен объему параллелепипеда построенного на векторах  . Ячейка Вигнера-Зейца повторяет симметрию обратной решетки, в то время как параллелепипед, построенный на векторах
. Ячейка Вигнера-Зейца повторяет симметрию обратной решетки, в то время как параллелепипед, построенный на векторах  не обладает симметрией обратной решетки.
не обладает симметрией обратной решетки.
 |
 ,
,  . Следовательно, собственные вектора обратной решетки
. Следовательно, собственные вектора обратной решетки 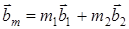 , где
, где 
Заштрихована элементарная ячейка обратной решетки.
 Видно, что обратная решетка имеет ось симметрии 6-го порядка. С другой стороны как видно ячейка Вигнера-Зейца представляет собой правильный шести угольник. В то время как элементарная ячейка построенная на векторах
Видно, что обратная решетка имеет ось симметрии 6-го порядка. С другой стороны как видно ячейка Вигнера-Зейца представляет собой правильный шести угольник. В то время как элементарная ячейка построенная на векторах  не обладает такой симметрией. Будем обозначать вектора, проводимые из центра ячейки Вигнера-Зейца в любую ячейку через
не обладает такой симметрией. Будем обозначать вектора, проводимые из центра ячейки Вигнера-Зейца в любую ячейку через  , они имеют размерность обратную длине. Два вектора
, они имеют размерность обратную длине. Два вектора  и
и  будем называть взаимно эквивалентными, если они отличаются друг от друга на какой-нибудь собственный вектор обратной решетки, т.е. если
будем называть взаимно эквивалентными, если они отличаются друг от друга на какой-нибудь собственный вектор обратной решетки, т.е. если 
 . По условию построения ячейки Вигнера-Зейца внутри нее нет взаимно эквивалентных векторов
. По условию построения ячейки Вигнера-Зейца внутри нее нет взаимно эквивалентных векторов  . Эквивалентные вектора имеются только на границе ячейки Вигнера-Зейца:
. Эквивалентные вектора имеются только на границе ячейки Вигнера-Зейца:
 ;
;  ;
;  .
.
Любые два вектора принадлежащие ячейке Вигнера-Зейца отличаются друг от друга не более чем на вектор  , таким образом, внутри себя ячейка Вигнера-Зейца содержит бесконечную совокупность неэквивалентных векторов. Совокупность неэквивалентных векторов образуют в обратном пространстве область, которая называется первой зоной Бриллюэна. Следовательно, первая зона Бриллюэна совпадает с ячейкой Вигнера-Зейца обратной решетки. Значит, первой зоне Бриллюэна принадлежат вектора
, таким образом, внутри себя ячейка Вигнера-Зейца содержит бесконечную совокупность неэквивалентных векторов. Совокупность неэквивалентных векторов образуют в обратном пространстве область, которая называется первой зоной Бриллюэна. Следовательно, первая зона Бриллюэна совпадает с ячейкой Вигнера-Зейца обратной решетки. Значит, первой зоне Бриллюэна принадлежат вектора  , которые короче всех эквивалентных векторов обратного пространства.
, которые короче всех эквивалентных векторов обратного пространства.
Докажем, что первой зоне Бриллюэна принадлежат вектора  , которые удовлетворяют неравенству:
, которые удовлетворяют неравенству:  ,
,  .
.
Доказательство: Исходя из построений ячейки Вигнера-Зейца, должно выполняться следующие неравенство:
 (1)
(1)
где  модуль проекции вектора
модуль проекции вектора  :
:  ,
,  - модуль проекции вектора
- модуль проекции вектора 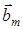 ,
, 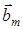 - собственные вектора проведенные в ближайшие к Г узлы. Очевидно (1) не измениться, если его правую часть умножить на модуль
- собственные вектора проведенные в ближайшие к Г узлы. Очевидно (1) не измениться, если его правую часть умножить на модуль 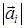 , тогда получаем:
, тогда получаем:
 (2)
(2)
 (3)
(3)

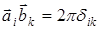 (4)
(4)
Для выполнения неравенства (3) в ряду  мы должны взять целое наименьшее число больше 0, то есть +1, тогда (3) примет вид:
мы должны взять целое наименьшее число больше 0, то есть +1, тогда (3) примет вид:
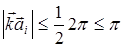 (4)
(4)  (5)
(5)
Если из точки Г провести прямые линии в следующие за ближайшими узлами узлы и через середины их провести перпендикулярные плоскости, то получим многогранник, если из него вычесть объем первой зоны Бриллюэна, то оставшийся объем образует вторую зону Бриллюэна и т.д. Для примера рассмотрим кристалл с плоской квадратной решеткой: а1 = а2 = а;  . Базисные вектора обратной решетки есть
. Базисные вектора обратной решетки есть  , и
, и  , значит обратная решетка плоской квадратной решетки является тоже квадратной.
, значит обратная решетка плоской квадратной решетки является тоже квадратной.
 |
§6. Связь между структурами прямой и обратной решеткой кристалла.
Сначала рассмотрим скалярное произведение собственного вектора прямой решетки  и собственного вектора обратной решетки
и собственного вектора обратной решетки 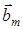 одного и того же кристалла, и учитывая что скалярное произведение их базисных векторов
одного и того же кристалла, и учитывая что скалярное произведение их базисных векторов 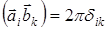 , получим:
, получим:
 (1)
(1)
С другой стороны
 (2)
(2)
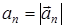 ,
, 
Из (2) следует что
 (3).
(3).
Если считать, что n = const, то проекция (3) определяет собой кристаллографическую плоскость перпендикулярную 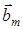 и отстающую от начальных координат на величину (3).
и отстающую от начальных координат на величину (3).
 Кристаллографическая плоскость – это такая плоскость, на которой находится бесконечное множество узлов кристаллической решетки. Из рисунка видно, что конец вектора
Кристаллографическая плоскость – это такая плоскость, на которой находится бесконечное множество узлов кристаллической решетки. Из рисунка видно, что конец вектора  лежит на плоскости (n), таким образом, на этой плоскости имеется хотя бы один узел. Покажем, что если имеется на этой плоскости хотя бы один узел (конец вектора
лежит на плоскости (n), таким образом, на этой плоскости имеется хотя бы один узел. Покажем, что если имеется на этой плоскости хотя бы один узел (конец вектора  ), то на этой плоскости имеется бесконечное множество других узлов, а это означает что плоскость кристаллографическая. Действительно, наряду с вектором
), то на этой плоскости имеется бесконечное множество других узлов, а это означает что плоскость кристаллографическая. Действительно, наряду с вектором  рассмотрим множество собственных векторов:
рассмотрим множество собственных векторов:
 , N – любое целое число,
, N – любое целое число,  .
.
Покажем, что вектора  дают с вектором
дают с вектором 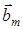 такое же скалярное произведение, что и с вектором
такое же скалярное произведение, что и с вектором  .
.

 Отсюда следует, что концы векторов
Отсюда следует, что концы векторов  также лежат на плоскости на которой лежит конец вектора
также лежат на плоскости на которой лежит конец вектора  , значит плоскость перпендикулярная вектору
, значит плоскость перпендикулярная вектору 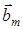 и отстоящая от начальных координат на величину (3) является кристаллографической. Так как N – любое целое число, то вектору
и отстоящая от начальных координат на величину (3) является кристаллографической. Так как N – любое целое число, то вектору 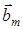 соответствует семейство параллельных плоскостей перпендикулярных вектору
соответствует семейство параллельных плоскостей перпендикулярных вектору 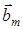 . Например, числу n+1 будет соответствовать другая плоскость перпендикулярная вектору
. Например, числу n+1 будет соответствовать другая плоскость перпендикулярная вектору 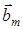 , которая отстоит от начала координат на величину
, которая отстоит от начала координат на величину  . Расстояние между соседними кристаллографическими плоскостями перпендикулярные вектору
. Расстояние между соседними кристаллографическими плоскостями перпендикулярные вектору 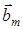 , очевидно равно
, очевидно равно  (4).
(4).
Используя вышеприведенные выводы для следующего: покажем, что кристаллографическая плоскость перпендикулярная вектору  имеет индексы Миллера (hkl) пропорциональные числам m1, m2, m3.
имеет индексы Миллера (hkl) пропорциональные числам m1, m2, m3.
Предположим, что кристаллографическая плоскость пересекает оси координат в точках с координатами:  ,
,  ,
,  . Пусть
. Пусть  - собственный вектор, конец которого лежит на этой плоскости. Вектора
- собственный вектор, конец которого лежит на этой плоскости. Вектора  - собственные вектора прямой решетки концы, которых лежат на данной кристаллографической плоскости. (n1, n2, n3 – целые числа). Обозначим через
- собственные вектора прямой решетки концы, которых лежат на данной кристаллографической плоскости. (n1, n2, n3 – целые числа). Обозначим через 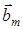 собственный вектор обратной решетки перпендикулярный данной кристаллографической плоскости. Этот вектор
собственный вектор обратной решетки перпендикулярный данной кристаллографической плоскости. Этот вектор 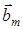 дает одинаковое скалярное произведение с вектором
дает одинаковое скалярное произведение с вектором  и с векторами
и с векторами  :
:
 (5)
(5)
С другой стороны
 ;
; 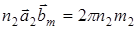 ;
;  . (6)
. (6)
Из (5) и (6) следует, что
 ;
;  ;
;  . (7)
. (7)
Из (7) следует, что
 (8)
(8)

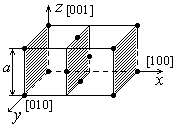 Из (8) получаем, что индексы Миллера данной кристаллографической плоскости кратны числам m1, m2, m3. После сокращения на общий множитель получаем истинные индексы Миллера. Используя вышеприведенные данные, найдем тип обратной решетки для данного типа прямой решетки. Предположим, что прямая решетка является кубической гранецентрированной. На рисунке заштрихованы кристаллографические плоскости перпендикулярные оси [011]. Расстояние между рассмотренными кристаллографическими плоскостями
Из (8) получаем, что индексы Миллера данной кристаллографической плоскости кратны числам m1, m2, m3. После сокращения на общий множитель получаем истинные индексы Миллера. Используя вышеприведенные данные, найдем тип обратной решетки для данного типа прямой решетки. Предположим, что прямая решетка является кубической гранецентрированной. На рисунке заштрихованы кристаллографические плоскости перпендикулярные оси [011]. Расстояние между рассмотренными кристаллографическими плоскостями  ,
, 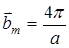 ,
,  . Также можно найти вектора
. Также можно найти вектора 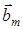 , которые параллельны двум другим ребрам и равные
, которые параллельны двум другим ребрам и равные 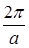 . Вектора
. Вектора 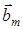 перпендикулярные друг другу, поэтому по этому обратная решетка кубическая. Плоскости <111> гранецентрированного куба перпендикулярны диагоналям куба и кристаллографические плоскости перпендикулярные диагоналям куба отстоят друг от друга на 1/3 часть диагонали куба.
перпендикулярные друг другу, поэтому по этому обратная решетка кубическая. Плоскости <111> гранецентрированного куба перпендикулярны диагоналям куба и кристаллографические плоскости перпендикулярные диагоналям куба отстоят друг от друга на 1/3 часть диагонали куба.  ,
,  ,
, 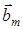 - параллелен главной диагонали куба, так как он перпендикулярен плоскостям <111>. Диагональ куба обратной решетки равна
- параллелен главной диагонали куба, так как он перпендикулярен плоскостям <111>. Диагональ куба обратной решетки равна  .
.
Видно, что  по величине в два раза меньше диагонали куба обратной решетки, значит, конец этого вектора приходится на центр куба, т.е. в центре куба обратной решетки имеется узел. Значит, обратная решетка для кристаллов кубической гранецентрированной системы является кубической объемно-центрированной и наоборот.
по величине в два раза меньше диагонали куба обратной решетки, значит, конец этого вектора приходится на центр куба, т.е. в центре куба обратной решетки имеется узел. Значит, обратная решетка для кристаллов кубической гранецентрированной системы является кубической объемно-центрированной и наоборот.
§7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
Прямая решетка кристалла характеризуется базисом  , а обратная решетка базисом
, а обратная решетка базисом 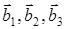 . Помимо базисных векторов введем ортогональную систему координат определяемую ортами i, j, k, при этом одну и ту же систему координат будем использовать как для прямой, так и для обратной решетки. Построим первые зоны Бриллюэна для таких типов кристаллических решеток, которые в основном определяют структуру кристаллических классов.
. Помимо базисных векторов введем ортогональную систему координат определяемую ортами i, j, k, при этом одну и ту же систему координат будем использовать как для прямой, так и для обратной решетки. Построим первые зоны Бриллюэна для таких типов кристаллических решеток, которые в основном определяют структуру кристаллических классов.
1. Простая кубическая решетка.
 Ее можно получить повторением в пространстве базисной ячейки куба со стороной а. В этом случае в качестве базиса удобно принять вектора
Ее можно получить повторением в пространстве базисной ячейки куба со стороной а. В этом случае в качестве базиса удобно принять вектора  обладающие свойством а1 = а2 = а3, α = β = γ = 900. Направим орты i, j, k вдоль ребер куба. Базис прямой решетки будет иметь вид:
обладающие свойством а1 = а2 = а3, α = β = γ = 900. Направим орты i, j, k вдоль ребер куба. Базис прямой решетки будет иметь вид:
 ,
,
 ,
,
 .
.

| […] | 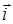
| 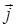
| 
|
| 
| - 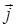
| |
| - 
| 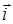
| |

| 
| - 
|
Найдем базис обратной решетки:
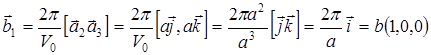


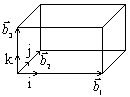 Ячейка, построенная на векторах
Ячейка, построенная на векторах 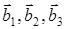 - это базисная ячейка обратной решетки, куб ребра которого направлены вдоль ортов. Объем этой ячейки будет совпадать с объемом первой зоны Бриллюэна.
- это базисная ячейка обратной решетки, куб ребра которого направлены вдоль ортов. Объем этой ячейки будет совпадать с объемом первой зоны Бриллюэна.
 .
.
Обратную решетку можно получить повторением в пространстве базисной ячейки простого куба со стороной 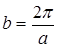 . Первую зону Бриллюэна будем находить как многогранник, построенный по известному правилу с центром в точке γ = Г. Для этого с какого-нибудь узла γ = Г проведем прямые отрезки в ближайшие узлы, через середины этих отрезков проведем плоскости. Получим многогранник со стороной
. Первую зону Бриллюэна будем находить как многогранник, построенный по известному правилу с центром в точке γ = Г. Для этого с какого-нибудь узла γ = Г проведем прямые отрезки в ближайшие узлы, через середины этих отрезков проведем плоскости. Получим многогранник со стороной 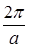 (куб). Значит, первая зона Бриллюэна кристалла с простой кубической решеткой есть куб со стороной
(куб). Значит, первая зона Бриллюэна кристалла с простой кубической решеткой есть куб со стороной 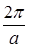 . Центр куба (γ = Г) будем принимать за начало отсчета, т.е. ей соответствует вектор
. Центр куба (γ = Г) будем принимать за начало отсчета, т.е. ей соответствует вектор  .
.
 На рисунке приведена зона Бриллюэна кристалла с простой кубической решеткой, на ней отмечены симметричные линии и симметричные точки. Симметричные линии (λ, Σ, Δ) проходят вдоль направлений <111>, <110>, <100> соответственно. Число линий λ = 8, Σ = 12, Δ = 6. Число симметричных точек R = 8 M = 12 и X = 6. Точки R имеют координаты типа
На рисунке приведена зона Бриллюэна кристалла с простой кубической решеткой, на ней отмечены симметричные линии и симметричные точки. Симметричные линии (λ, Σ, Δ) проходят вдоль направлений <111>, <110>, <100> соответственно. Число линий λ = 8, Σ = 12, Δ = 6. Число симметричных точек R = 8 M = 12 и X = 6. Точки R имеют координаты типа  . Точки X имеют координаты типа
. Точки X имеют координаты типа 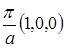 . Точки M имеют координаты типа
. Точки M имеют координаты типа  .
.
Дата добавления: 2015-10-13; просмотров: 355 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Введение. | | | УТВЕРЖДАЮ |