Билет № 23

2) ВОПРОС св-ва опр инт и теор о среднем ОТВЕТ 1! Если 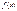ингегр в 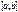то она интегр. и в промеж 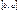, причем 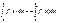по опр интегр. при 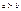в предполож. что интегр. сущ. также по опр полаг. 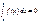2! Пусть 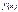интегр в наиб из промеж 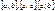то она интегр и в двух других и имеет место при любом располож. точек 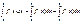ДОКАЗ. Положим 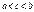и ф-ция интегр. в 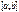Рассмотр. разбиен в 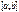на части, причем 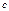одна из т. делен 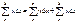ввиду положит.всех слаг.из стремл. к 0 сумм слева следует то же и для правых сумм, так что инт-мость 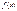в промеж 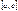и 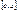установл. очевидно 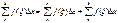переходя к пред. при 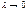получ требуемое рав-во.

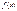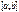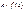
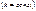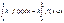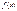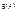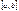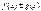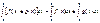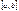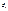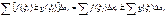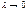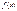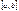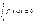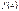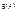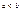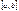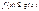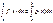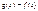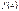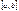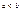3! Если интегр. в , то и также интегр. и 4! Если и интегр в то тоже интегр причем ДОКАЗ. Разобъем на чясти и сост. интегр суммы причем т. на кажд. промеж выбир. произв-но но для всех сумм одни и те же Переходя к пред и приход. к требуем. соотн. 5! Если интегр-ая на неотр. то 6! Если и и интегр. на и то и Применить (5) к 7! Пусть интегр в и тогда 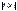интегр. и имеет место 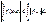ДОКАЗ. Убедимся в 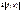. Если в промеж. 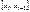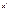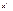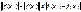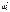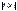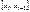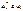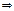взять любые и то обозн через колеб-е в имеем 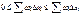стремл к 0 суммы справа влечет то же слева Самое нер-во получ из 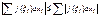и пер-дя к пред

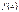8! Если интегр в 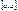где 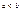и если во всем промеж имеет мес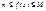то то 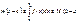ДОКАЗ 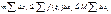и перейти к пределу. 9!Теор. о средн. значении.Пусть 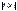интегр. на 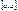и пусть во всем промеж.

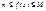тогда 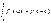где 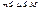ДОКАЗ. Если 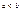то по св (8) имеем 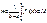положив 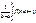получ требуем. рав-во.Если 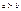, проводим то же рассужд. для 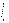ф затем, переставив

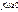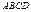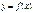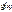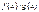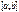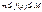пределы переходим к прежней ф-ле. Геометр Пусть . Рассмотр. кривол-ную ф-ру под кривой тогда площ. выражен. кривол. интегр. = площ. прямоуг. с тем же основ и с некотор. ордин в качестве высоты. 10! Пусть1) и интегр в 2) 3) 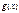не меняет знака 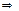о.требуем. промеж. меет место е слева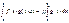

4)

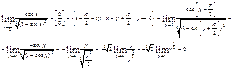
5)

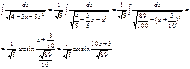
Дата добавления: 2015-10-13