
Билет №1
3) 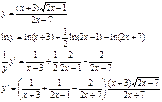
4) 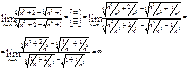
5) 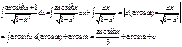
Билет № 2
3) 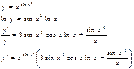

4) 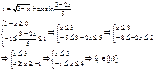
| x | 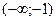
| (-1) | (-1;0) | 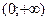
| |

| --- | --- | 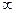
| + | |
| y | ♀ | ♀ | max | ♂ |
5)

Билет № 3
3) 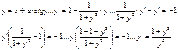
4) 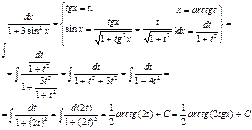
5) 
Билет № 4
3)

4)
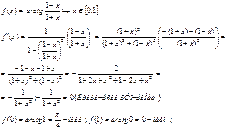
5)
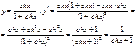
Билет № 6
3) 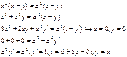
4) 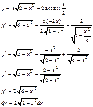
5) 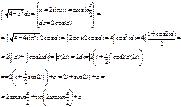
Билет № 8
3) 
4) 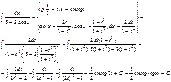
5) 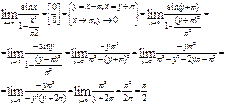
Билет № 7
3)
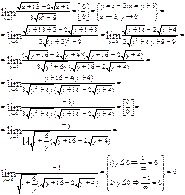
4) 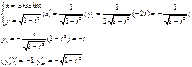
5)
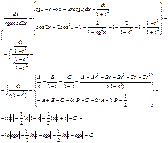
Билет № 9
3) 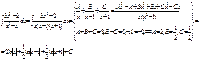
4) 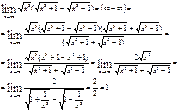
5) 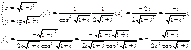
Билет № 11
3) 
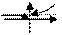
4) 
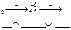
5) 
Билет № 13
3) 
4) 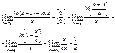
5)
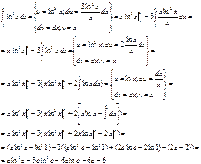
Билет № 14
3) 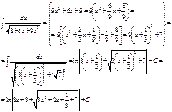
или
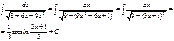
4) 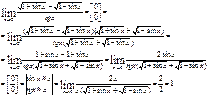
5)
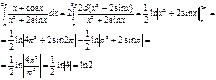
Билет № 15
3) 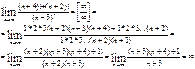
4) 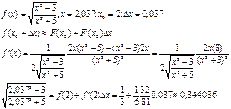
или
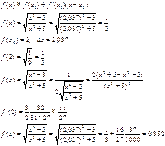
5)
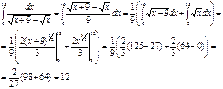
Билет № 16
3)

4)
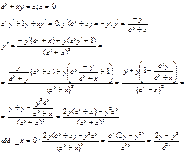
5) 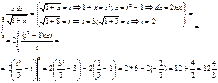
Билет № 18
3) 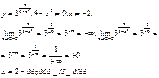
4) 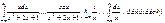
5)
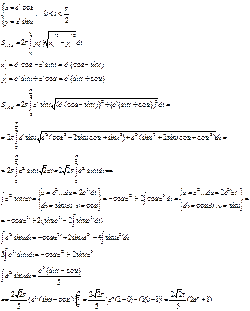
Билет № 19
3) 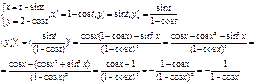
4) 
5) 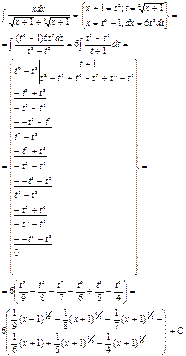
Билет № 21
3)

4) 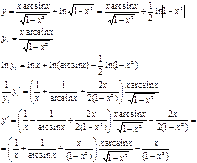
5) 
Билет № 22
3) 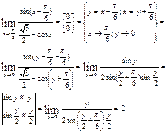
4) 
5)  !!!!
!!!!
!!!
Билет № 24
3) 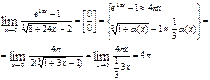
4) 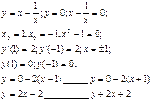
5) 
Билет № 25
3) 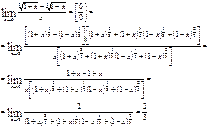
4) 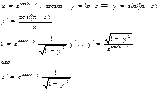
5) 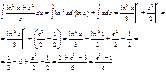
или
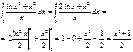
Билет № 12
3) 
4) 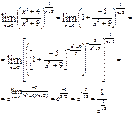
Билет № 5
1)  ВОПРОС Предел монотонной ф-ции 1 и 2 замеч. пределы. ОТВЕТ Пусть дана монот. возр. посл
ВОПРОС Предел монотонной ф-ции 1 и 2 замеч. пределы. ОТВЕТ Пусть дана монот. возр. посл 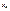 . Если она огранич. сверху:
. Если она огранич. сверху: 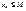 то необход. имеет конечн.предел, иначе она
то необход. имеет конечн.предел, иначе она 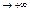 .ДОКАЗ Допустим что переменная огранич. сверху, тогда для множ
.ДОКАЗ Допустим что переменная огранич. сверху, тогда для множ 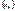 ее знач. должна сущ. и конеч. верхн. граница
ее знач. должна сущ. и конеч. верхн. граница 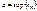 именно это число и будет пред. посл. Действ.,во-первых для всех знач.
именно это число и будет пред. посл. Действ.,во-первых для всех знач. 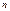 будет
будет 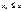 во-вторых какое бы ни взять
во-вторых какое бы ни взять 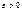 найд. такое знач
найд. такое знач 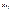 которое превзойд.
которое превзойд. 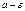 ,
, 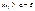 .Так как ввиду монот. перем, при
.Так как ввиду монот. перем, при 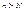 будет
будет 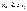 т.е. и подавно
т.е. и подавно  , то для этих знач номера
, то для этих знач номера 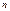 выполн. нерав-ва
выполн. нерав-ва 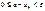 так что
так что 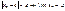 ч.т.д.Пусть послед.не огран.сверху,тогда сколь ни велико было бы
ч.т.д.Пусть послед.не огран.сверху,тогда сколь ни велико было бы 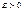 найдется хоть одно знач. посл. большее
найдется хоть одно знач. посл. большее 
 ,ввиду монот.
,ввиду монот. 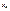 для
для 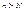 и подавно
и подавно 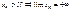 1 ЗАМЕЧ
1 ЗАМЕЧ 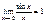 || докажем
|| докажем  при
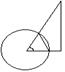
при  (1) для этого в круге радиуса
(1) для этого в круге радиуса 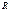 рассмотр
рассмотр 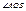 хорду
хорду 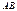 и касат.
и касат.  к окр.в т.
к окр.в т. 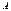 . Имеем
. Имеем 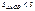 сект.
сект. 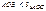 .Радианн.меру
.Радианн.меру 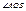 обозн.за
обозн.за 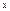 т.что длина дуги
т.что длина дуги 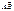 =
= 

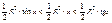 сокр.на
сокр.на 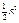 и разделим
и разделим 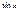 на кажд.из членов. нер-ва
на кажд.из членов. нер-ва 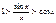 ;
; 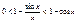 но
но 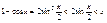 в силу (1)
в силу (1) 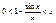
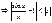 это нер-во и реш. вопрос. 2 ЗАМЕЧ
это нер-во и реш. вопрос. 2 ЗАМЕЧ 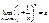 ДОКАЗ:
ДОКАЗ: 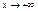 . кажд.знач.закл. между 2 плож. цел.числами
. кажд.знач.закл. между 2 плож. цел.числами 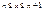
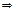 выполн. нерав.
выполн. нерав. 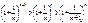 если
если 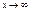 то и
то и 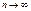 найдем
найдем 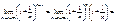
= 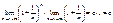 ;
; 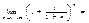
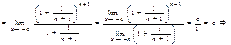
 Пусть
Пусть 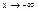 введем
введем 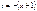 или
или 
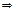
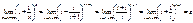 чтд
чтд
2) ВОПРОС Опр.интегр.и способы его вычисл. Определ. Пусть задана 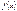 на
на 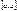 .Разобьем произв. этот промеж.
.Разобьем произв. этот промеж. 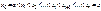 Наиб.из разност.
Наиб.из разност. 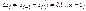 будем обозн.
будем обозн. 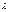 возьмем в кажд. из промеж.
возьмем в кажд. из промеж. 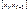 произв. точку
произв. точку 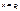 ;
; 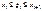 и состав. сумму
и состав. сумму  Установ. понятие кон. предела
Установ. понятие кон. предела 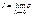 Представим себе бескон. число рабиен.
Представим себе бескон. число рабиен. 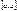 тогда
тогда 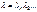 сход.к нулю.
сход.к нулю. 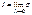 понимаем:что посл. знач. суммы
понимаем:что посл. знач. суммы 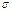 отвеч. любой основ. послед. разбиений промеж.всегда сход. к пределу
отвеч. любой основ. послед. разбиений промеж.всегда сход. к пределу 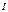 как ни выбир. при
как ни выбир. при 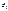 . Кон. предел
. Кон. предел 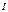 суммы
суммы 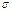 при
при 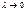 есть опр. интегр ф-ции
есть опр. интегр ф-ции 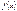 в промеж от
в промеж от 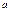 до
до 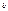
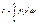 если предел сущ то
если предел сущ то 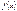 назыв интегрируем в промеж
назыв интегрируем в промеж 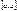 Числа
Числа 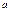 и
и 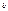 есть нижн и верх пределы ентеграла. Методы выч: осн ф-ла
есть нижн и верх пределы ентеграла. Методы выч: осн ф-ла 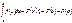 (А) Замена переменной Пусть надо выч.
(А) Замена переменной Пусть надо выч. 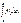 где
где 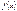 непр на
непр на 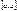 Положим
Положим 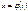 подчинив ее услов.1)
подчинив ее услов.1)  опр и непр на
опр и непр на 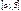 ее знач не выход пред промеж
ее знач не выход пред промеж 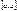 , когда
, когда 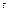 измен
измен 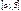 2)
2) 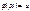 ,
, 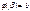 3)сущ в
3)сущ в 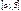 непр произ
непр произ  тогда имеет место
тогда имеет место  имеем одновр
имеем одновр 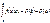
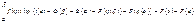 По частям
По частям 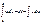 в предпол. что ф-ции
в предпол. что ф-ции 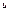 ,
,  от независ. перем.
от независ. перем. 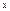 непр. в рассм. промеж.
непр. в рассм. промеж. 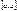 вместе с произв.Обозн. посл инт. через
вместе с произв.Обозн. посл инт. через 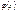 тогда по ф-ле (А)
тогда по ф-ле (А)  в то же время в силу (А)
в то же время в силу (А) 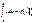 имеем оконч.
имеем оконч. 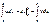
3) 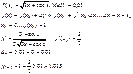
5)

Дата добавления: 2015-10-13; просмотров: 98 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Речная долина и ее элементы | | | Билет № 23 |