
Читайте также:
|
Расчетная часть
1.2.1. Конструктивный расчет
Определение шага м
h=(0,1…..1)*D, (1)
где h-шаг м,
D-диаметр вала шнека м,
h=0,8·0,15=0,12 м
d пред=  .f м, (2)
.f м, (2)
где коэффициент внутреннего трения ƒ = 0,3 [1]
dпред – предельный диаметр м,
dпред=  <0,15 м
<0,15 м
Определение угла подъема витка,град:
αD=arctg 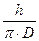 (3)
(3)
αD=arctg 
αd=arctg  (4)
(4)
αd=arctg 
αo=  (5)
(5)
αo= 
Определение коэффициента потерь
Ко= 1 - (cos2αо – 0,5·f·sin2αо), (6)
Ко= 1 – (cos2 32,3– 0,5·0,3·sin 2·32,3)= 0,279
Изгибающий момент в витке шнека, 
Ми =  , (7)
, (7)
а=  =
=  (8)
(8)
где а – геометрический коэффициент
Р – давление Па,
Ми – изгибающий момент в витке шнека  ,
,
Ми= 
Определение толщины витка, мм:
 (9)
(9)
где [σ] – допускаемое напряжение материала лопасти шнека берем по стали 40ХГС [3]
 , δ=4 мм=0,004м
, δ=4 мм=0,004м
Площадь цилиндрической поверхности, м2:
Fц= 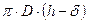 (10)
(10)
Fц=3,14·0,15·(0,12-0,004)=0,054 м2
Длина винтовой линии в пределах одного шага, м:
l=  (11)
(11)
l= 
L=  (12)
(12)
L= 
где l – длина винтовой линии у основания м,
L – длина винтовой линии на витке лопасти м
Площадь поверхности витка шнека, м2:
Fм=  (13)
(13)

Определение частоты вращения вала, об/с:
 , (14)
, (14)

где ρ- плотность продукта
ρ=ρпр·0,7 кг/м³, ρпр=900 кг\м3  ,
,
ρ=900·0,7=630 кг\м3,
Q- производительность кг\с
Осевое усилие,  :
:
 (15)
(15)

Крутящий момент,  :
:
Мкр=  (16)
(16)
Мкр= 
Определение напряжения на витке лопасти
Осевое напряжение, МПа:
 , (17)
, (17)

где σи – изгибающее напряжение МПа
 МП (18)
МП (18)
где τ – напряжение кручения МПа
 ,м³ (19)
,м³ (19)

 , (20)
, (20)

где b-высота лопасти,м
m- число витков,

эквивалентное напряжение, МПа

 (21)
(21)


где σ – осевое напряжение МПа
суммарное напряжение, МПа:
 (22)
(22)
где σи – изгибающее напряжение МПа
σэкв – эквивалентное напряжение МПа
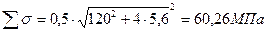
Число заготовок лопастей и их геометрические размеры
- угол выреза в кольце заготовки

(23)

- наружный диаметр развертки, м:
 (24)
(24)

- внутренний диаметр развертки, м:
 (25)
(25)

- уточненный средний шаг витка, м:
 (26)
(26)

- уточненная длинна люка, м:
L'=H·m (27)
L'=0,126·4=0,504 м
1.2.2. Расчет реологических характеристик
Определение коэффициента динамической вязкости
 (28)
(28)
где К1,К2- коэффициент подобия
Q – производительность кг/с
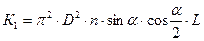 , м³ (29)
, м³ (29)
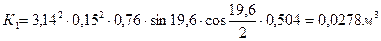
 (30)
(30)
где е - зазор между корпусом и витками
l – длина рабочей камеры, м;
μ – коэффициент динамической вязкости, Па·с
P – давление в камере, Па;
n - частота вращения шнека, об/с
 , (31)
, (31)


Тогда, подставляя известные значения в формулу производительности:
 ,
,

 , выражаем коэффициент динамической вязкости: μ =10,3 Па·с
, выражаем коэффициент динамической вязкости: μ =10,3 Па·с
Определяем коэффициент бокового давления и уточняем величину осевого и бокового давлений по длине канала:
 (32)
(32)
(33)
 (34)
(34)

где а1 – коэффициент гомогенности;
a1=а2 · dn-2, (35)
а1=0,005·0,041,67-2=0,0144
а2=0,005, n=1,67 – эмпирические коэффициенты
Расчет ядра сечения производим, исходя из уравнения Букингема-Рейнера:

(36)
где θ – напряжение сдвига
 (37)
(37)
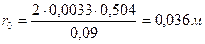
где r - радиус ядра сечения м.
1.2.3. Тепловой расчет
Конечная температура продукта при отсутствииохладителя:
t11 = t0 · eР 
 (38)
(38)

Удельный тепловой поток, передаваемый материалом корпусу экструдера:
 (39)
(39)
где t0 t1 – начальная и конечные температуры продукта, ºС
F – площадь поверхности контакта продукта с корпусом экструдера м;
с – теплоемкость экструдируемого материала с = 5130 Дж [1]
 (40)
(40)
Коэффициент теплопередачи определим по формуле для плоской стенки, так как dвн / dн = 150/162 = 0,92>0,5
 (41)
(41)
где α1 - коэффициент теплоотдачи от хладагента к стенке корпуса при температуре пленки хладагента

(42)
температура пленки хладагента:
 (43)
(43)

константа режима течения хладагента:
А = 280 · 103 – ламинарный режим
А = 660 · 103 – переходный режим
А = 990 · 103 – турбулентный режим
При этом режим определяем по критерию Рейнольдса:

(44)
Температурой стенки корпуса экструдера со стороны хладагента tст1 вначале задаемся, принимая ее равной средней температуре экструдата, а скорость движения хладагента w принимаем равной 1 м/с.
 (45)
(45)
где ∆t – температурный напор;
r – скрытая теплота парообразования при температуре стенки корпуса, кДж/кг r = 2458 кДж/кг [2]
Удельная тепловая нагрузка при подводе хладагента:
 (46)
(46)
Действительную температуру стенки tст1 определяем графоаналитическим методом исходя из того, что при установившемся теплообмене, количество тепла, передаваемое стенке от хладагента qхл должно равняться количеству тепла, передаваемому через стенку теплопроводностью qст , а также количеству тепла, передаваемому от стенки трубы к охлаждаемому экструдату qс. При правильно выбранной tст1 :
qхл = qст = q
 (47)
(47)
 (48)
(48)
При вычислении общего термического сопротивления:
 (49)
(49)
Принимаем тепловую проводимость загрязненной стенки со стороны хладагента, со стороны экструдата и проводимость самой стенки:
 (50)
(50)
(51)
Тогда  (52)
(52)
 (53)
(53)
Так как qст > qхл, то уточняем конечную температуру стенки:
 (54)
(54)
Тогда коэффициент теплопередачи от продукта к стенке:

(55)
Коэффициент теплопередачи:

Количество хладагента:
 (56)
(56)

где с = 4,19  - теплоемкость воды;
- теплоемкость воды;
∆t – разность температуры воды на входе и выходе рубашки.
Продолжительность теплообмена:

 (57)
(57)
Скорость движения воды:
(58)
Для ламинарного режима течения эквивалентное сечение течения хладагента в зазоре водяной рубашки
 (59)
(59)
где υ – скорость течения хладагента, м/с
Re – критерий Рейнольдса для обтекания плоской стенки;
ρв, μв, υ – плотность, динамическая, кинематическая вязкость воды.
 (60)
(60)
Внутренний диаметр водяной рубашки:
 (61)
(61)
где Dн – наружный диаметр корпуса, м
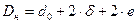 м (62)
м (62)

1.2.4. Подбор сечения матрицы
Расчет сечения производим по постарению расходно-напорной характеристике
 (63)
(63)
где  - коэффициент формы сечения матрицы, м3 (64)
- коэффициент формы сечения матрицы, м3 (64)
F – площадь поперечного сечения канала, м2
L,, - длинна канала или толщина матрицы, выбираемая в зависимости от вида сырья и диаметра камеры для молочного сырья (5…10)·10-3
П – периметр канала, м
 м (65)
м (65)

 м2 (66)
м2 (66)
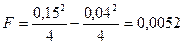 м2
м2
 м3
м3
 - круглое сечение; (67)
- круглое сечение; (67)
где Dк – суммарный диаметр канала для молочного сырья (3…7)·10-3 м
 - коническое сечение; (68)
- коническое сечение; (68)
где Dнач, Dкон – начальный и конечный диаметры канала, м;
 - кольцевое сечение; (69)
- кольцевое сечение; (69)
где Rн, Rв – наружный и внутренний радиусы канала, м;
 - щелевое сечение; (70)
- щелевое сечение; (70)
где bк, hк - ширина и высота канала сечения матрицы, м;
ƒ – удельная площадь поперечного сечения канала (ƒ=0,5).
Так как коэффициент формы сечения матрицы во всех случаях имеет одну величину, то, вычислив геометрические характеристики матрицы с круглым сечением каналов, методом подбора определяются геометрические характеристики каналов других сечений.
Производим расчет матрицы с каналами круглого сечения:
(71) 
Так как для молочного сырья длина матрицы составляет (5…!0)·10-3 м, то, исходя из заданного диаметра шнековой камеры, принимаем длину равную 10 мм. Тогда суммарный диаметр каналов матрицы 0,04 м. Приняв диаметр одного формующего отверстия матрицы равным 1,5мм, определяем их количество как отношение суммарного диаметра к диаметру одного отверстия. В результате их количество равно 27 шт.
Граничные условия для матрицы с коническими отверстиями
 (72)
(72)


Граничные условия для матрицы с кольцевыми отверстиями:
 Rн=1,3 · Rв
Rн=1,3 · Rв
 (73)
(73)
В итоге Rв1= 0,73 мм Rв2= 0,95мм.
Граничные условия для матрицы с щелевыми отверстиями:
 bк = 0,5 · hк
bк = 0,5 · hк
 (74)
(74)
В итоге bк= 0,025 мм hк=0,05 мм
Так как bк < 0,05мм и hк  0,05мм в связи с этим производство матрицы с щелевым отверстием невозможен.
0,05мм в связи с этим производство матрицы с щелевым отверстием невозможен.
 ,
,  (75)
(75)
ВАРИАНТЫ ЗАДАНИЙ К РАСЧЕТУ
ПО ТЕМЕ:
Дата добавления: 2015-10-13; просмотров: 175 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Введение | | | Мѣра названия |