Раскраска графов. Проблема четырех красок

Определение 2.25. Раскраской графа называется такое приписывание цветов (натуральных чисел) его вершинам, что никакие две смежные вершины не получают одинаковый цвет. Раскраска графа в m цветов называется m - раскраской.

Определение 2.26. Наименьшее возможное число цветов m в раскраске графа G называется хроматическим числом и обозначается .

Очевидно, что существует m -раскраска графа G для любого m в диапазоне .

Определение 2.27. Множество вершин, покрашенных в один цвет, называется цветовым классом. Никакие две вершины в цветовом классе не смежны.

Нахождение хроматического числа достаточно трудоёмкая задача. Однако можно дать оценку этого числа. Так, например, из определения хроматического числа вытекает его оценка от количества ребер:

.

Доказательство: Пусть граф G имеет хроматическое число . Тогда G содержит, по меньшей мере, одно ребро, инцидентное вершинам из разных цветовых классов, или один и тот же цвет можно использовать для двух различных цветовых классов. Пары вершин из k различных цветовых классов можно выбрать 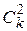способами, поэтому . Решая это неравенство относительно k, получаем требуемое утверждение. 

Примеры. , , 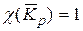, , , . Для графа на рис. 2.22 (его раскраска изображена на рисунке 2.23).

Рис. 2.22 Рис. 2.23

Для более общих случаев верна следующая теорема.

Теорема об оценке хроматического числа. .

Доказательство: Индукция по числу вершин p.

1) Если , то и .

2) Допустим, что неравенство верно для всех графов с числом вершин меньше, чем p. Рассмотрим граф G (V, E) с p вершинами. Тогда для v ÎV . Но , значит, хотя бы один цвет в -раскраске графа G \ v свободен для v. Покрасив v в этот цвет, получим -раскраску графа G. 

Исторически раскрасочная терминология пришла в теорию графов из задачи о раскраске стран на карте: “Сколько цветов требуется для раскраски различных стран на карте так, чтобы каждые 2 смежные страны были окрашены по-разному?” Эта задача сводится к проблеме определения максимального хроматического числа плоских графов. По одним сведениям, об этой задаче знал еще в 1840 г. немецкий математик Мёбиус. По другим же данным она возникла в 1852 г., когда некий Франсис Гатри спросил своего брата Фредерика, в то время студента-математика в Кембридже, верно ли, что каждую карту можно окрасить в четыре цвета так, чтобы смежные страны имели разные цвета. Эта задача, получившая название проблемы (гипотезы) четырех красок, была впервые предложена вниманию общественности в выступлении Кэли на заседании Лондонского математического общества в 1878 г.

Теорема о 4 красках. Всякий плоский граф можно раскрасить четырьмя красками.

Годом позже А. Кемпе опубликовал неправильное доказательство, которое было в 1890 г. переделано Р. Хивудом в доказательство теоремы о пяти красках.

Теорема о пяти красках. Всякий плоский граф можно раскрасить пятью красками.

Доказательство: Достаточно рассматривать связные графы, потому что . Индукция по числу вершин p.

1) Если , то .

2) Пусть теорема верна для всех связных планарных графов с p вершинами. Рассмотрим связный планарный граф G с p +1 вершиной. В графе G $ v Î V 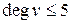(см. задачу 53). По индукционному допущению . Нужно раскрасить вершину v.

а) Если , то в 5-раскраске G \ v существует цвет, свободный для v.

б) Если и для раскраски вершин, смежных с v, использованы не все 5 цветов, то в 5-раскраске G \ v также существует цвет, свободный для v.

в) Осталось рассмотреть случай, когда и все 5 цветов использованы для раскраски вершин, смежных с v (вершина v_i покрашена в цвет i). Пусть G ₁₃ – правильный подграф графа G \ v, порожденный всеми вершинами, покрашенными в цвета 1 или 3 в 5-раскраске графа G \ v. Если v ₁ и v ₃ принадлежат разным компонентам связности графа G ₁₃, то в той компоненте, в которой находится v ₁, произведем перекраску 1«3. При этом получится 5-раскраска G \ v, но цвет 1 будет свободен для v. В противном случае существует простая цепь, соединяющая v ₁ и v ₃ и состоящая из вершин, покрашенных в цвета 1 и 3. В этом случае v ₂ и v ₄ принадлежат разным компонентам связности подграфа G ₂₄, так как граф G – планарный (рис. 2.24). Перекрасим вершины 2«4 в той компоненте связности графа G ₂₄, которой принадлежит v ₂, и получим 5-раскраску графа G \ v, в которой цвет 2 свободен для v. 

Рис. 2.24

В 1880 г. Тейт анонсировал “дальнейшие доказательства” гипотезы четырех красок, которые так и остались нематериализованными.

В 1941 г. Брукс улучшил оценку для хроматического числа некоторых графов.

Теорема Брукса. Если связный граф G не является ни полным графом, ни нечетным циклом, то .

В середине ХХ века при попытке решить проблему 4 красок были доказаны следующие теоремы.

Теорема Татта (1956 г.). Всякий 4-связный планарный граф имеет гамильтонов цикл (Гипотеза, содержащая формулировку этой теоремы, была высказана в 1946 г.).

Теорема Грёцша (1959 г.). Каждый плоский граф, не содержащий треугольника, можно раскрасить тремя красками.

Тем не менее доказать теорему о 4 красках не могли в течение 125 лет после ее первоначальной формулировки и в течение 99 лет после ее формулировки для научной общественности.

Первое общепризнанное доказательство теоремы о четырех красках было опубликовано Аппелем и Хакеном в 1977 г [7]. Доказательство основано на идеях, восходящих еще к статье Кемпе и далеко продвинутых Биркгофом и Хеешем. Говоря очень приблизительно, доказательство сводится, во-первых, к утверждению, что каждая плоская триангуляция (т.е. плоский связный граф, каждая грань которого, включая и внешнюю, ограничена циклом длины 3) должна содержать, по крайней мере, одну из 1482 «неизбежных конфигураций» (конфигурация – это связный подграф плоского графа). На втором этапе с помощью компьютера показывается, что каждая из этих конфигураций «редуцируема», т. е. что любая плоская триангуляция, содержащая такую конфигурацию, может быть 4-раскрашена, исходя из 4-раскрасок меньших триангуляций. Вместе взятые эти два шага составляют индуктивное доказательство того, что все плоские триангуляции, а следовательно, и все плоские графы можно раскрасить в четыре цвета.

Доказательство Аппеля и Хакена не было обойдено критикой, и не только из-за использования ими компьютера. Авторы ответили 741-страничной алгоритмической версией доказательства, которая учитывает различные критические замечания и исправляет множество ошибок (например, ими добавлено еще 450 конфигураций к «неизбежному» списку) [14]. В результате, компьютер, проработав 1500 часов, показал, что из 1932 конфигураций 1931 редуцируема. Последнюю конфигурацию исследовали вручную, применив более тонкие методы редукции, не заложенные в программу. Проверка показала, что и эта конфигурация редуцируема. Так проблема четырех красок была решена.

Гораздо более короткое доказательство, которое основано на тех же идеях (и, в частности, использует компьютер таким же образом), но более доступно проверке как в текстовой, так и в компьютерной части, дано в статье [15].

Замечание. Вданном параграфе речь шла о вершинной раскраске графа. Но также существует и понятие реберной раскраски – такое приписывание цветов (натуральных чисел) ребрам графа, что никакие два смежных ребра не получают одинаковый цвет. Наименьшее возможное число цветов m в реберной раскраске графа G называется реберным хроматическим числом или хроматическим индексом и обозначается . Очевидно, что для любого графа . Этот результат уточняют 2 следующие теоремы.

Теорема Кёнига (1916 г.). Для каждого двудольного графа .

Теорема Визинга (1964 г.). Для каждого графа .

Таким образом, если для имеются лишь приблизительные оценки, то родственное ему число может принимать лишь 2 значения.

К сожалению, не существует эффективных алгоритмов (т.е. имеющих полиномиальную сложность) решения задач нахождения минимальной раскраски вершин и ребер графа. Разработаны лишь алгоритмы нахождения минимальной раскраски произвольного графа, основанные на переборе возможных вариантов, и алгоритмы с полиномиальной сложностью, приводящие к раскраске, близкой к минимальной [6].

Наши рекомендации по нахождению хроматического числа и хроматического индекса состоят в следующем. Вычисление целесообразно начинать с выделения в графе максимального полного подграфа – количество вершин в нем будет минимально возможным значением . Нахождение лучше начинать с определения вершины максимальной степени и раскраски инцидентных ей ребер. Дальнейшую раскраску вершин (или ребер) следует производить, исходя из экономии цветов, т.е. 2 несмежные между собой вершины (ребра), но смежные третьей вершине (ребру), раскрашивать одним цветом.

СПИСОК ЛИТЕРАТУРЫ

1. Алексеев В.Е. Элементы теории графов. Пособие для студентов заочного отделения. – Н.Новгород, ННГУ, 2002.

2. Берж К. Теория графов и ее применения. – М.: Изд. иностр. лит., 1962.

3. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. - М.: Наука, 1977.

4. Дистель Р. Теория графов. Новосибирск, Изд-во Института математики, 2002.

5. Евстигнеев В.А. Применение теории графов в программировании. - М.: Наука, 1985.

6. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука, 1990.

7. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. М.: Энергоатомиздат, 1988. 2-е изд., переработанное и дополненное.

8. Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учеб. пособие. - М.: Изд-во МАИ, 1992.

9. Новиков Ф.А. Дискретная математика для программистов. СПб: Питер, 2001.

10.Оре О. Теория графов. 2-е изд. — М.: Наука. 1980. — 336 с.

11.Уилсон Р. Введение в теорию графов. – М.: Мир, 1977.

12.Харари Ф. Теория графов. – М.: Мир, 1973.

13.Шапорев С.Д. Математическая логика. Курс лекций и практических занятий: Учеб. пособие. - СПб: БХВ-Петербург, 2005. – 416 с.

14.Appel K., Hakeп W.Every Planar Map is Four Colorable. Providence: Amer. Math. Soc. 1989.

15.Robertson N., Sanders D., Seymour P.D., Thomas H. The four-colour theorem // J. Combin. Theory. Ser. B. 1997. V. 70. P. 2-44.

Дата добавления: 2015-10-13