
Читайте также:
|
Индивидуальное задание 1 МК3
Задача 1. Найти область определения указанных функций
1.1. 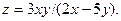
| 1.2. 
|
1.3. 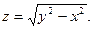
| 1.4. 
|
1.5. 
| 1.6. 
|
1.7. 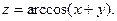
| 1.8. 
|
1.9. 
| 1.10. 
|
1.11. 
| 1.12. 
|
1.13. 
| 1.14. 
|
1.15. 
| 1.16. 
|
1.17. 
| 1.18. 
|
1.19. 
| 1.20. 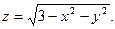
|
1.21. 
| 1.22. 
|
1.23. 
| 1.24. 
|
1.25. 
| 1.26. 
|
1.27. 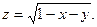
| 1.28. 
|
1.29. 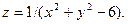
| 1.30. 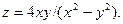
|
Задача 2. Вычислить значения частных производных 
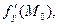
 для данной функции f(х, у, z) в точке М0(х0, у0, z0) с точностью до двух знаков после запятой
для данной функции f(х, у, z) в точке М0(х0, у0, z0) с точностью до двух знаков после запятой
2.1. f(x, y, z) =  ,
М0(0, -1, 1). ,
М0(0, -1, 1).
| 2.2. f(x, y, z) = 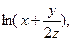 М0(1,2,1).
М0(1,2,1).
|
2.3. f(x, y, z) =  ,
М0(p/6, 1, 2). ,
М0(p/6, 1, 2).
| 2.4. f(x, y, z) = ln(x3+2у3-z3), М0(2, 1, 0). |
2.5. f(x, y, z) =  ,
М0(1, 0, 1). ,
М0(1, 0, 1).
| 2.6. f(x, y, z) =  М0(0, 0,
М0(0, 0,  ). ).
|
2.7. f(x, y, z) =  ,
М0(3, 4, 2). ,
М0(3, 4, 2).
| 2.8. f(x, y, z) =  ,
М0(2, 1, 0). ,
М0(2, 1, 0).
|
2.9. f(x, y, z) =  ,
М0(2, 5, 0). ,
М0(2, 5, 0).
| 2.10. f(x, y, z) =  М0(2, 0, 4).
М0(2, 0, 4).
|
2.11. f(x, y, z) =  М0(-1, 1, 0).
М0(-1, 1, 0).
| 2.12. f(x, y, z) =  ,
М0(2, 1, 1). ,
М0(2, 1, 1).
|
2.13. f(x, y, z)=  М0(1,1/2, p).
М0(1,1/2, p).
| 2.14. f(x, y, z) =  ,
М0(1, 1, 2). ,
М0(1, 1, 2).
|
2.15. f(x, y, z)=  М0(1, 2, 2).
М0(1, 2, 2).
| 2.16. f(x, y, z)=  М0(5,2,3)
М0(5,2,3)
|
2.17. f(x, y, z) = 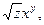 М0(1, 2, 4).
М0(1, 2, 4).
| 2.18. f(x, y, z) =  М0( М0(   ). ).
|
2.19. f(x, y, z) =  М0(2, 1, 8).
М0(2, 1, 8).
| 2.20. f(x, y, z) =  М0(2, 3, 25).
М0(2, 3, 25).
|
2.21. f(x, y, z) =  М0(3, 2, 1).
М0(3, 2, 1).
| 2.22. f(x, y, z) =  М0(1, 1, 1).
М0(1, 1, 1).
|
2.23. f(x, y, z) =  М0(3, 0, 1).
М0(3, 0, 1).
| 2.24. f(x, y, z) = 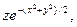 М0(0, 0, 1).
М0(0, 0, 1).
|
2.25. f(x, y, z) =  М0(
М0( , ,  , ,  ). ).
| 2.26. f(x, y, z) =  М0(4, 1, 4).
М0(4, 1, 4).
|
2.27. f(x, y, z) =  М0(3, 1, 1).
М0(3, 1, 1).
| 2.28. f(x,y,z)=  М0(3,4,
М0(3,4,  ). ).
|
2.29. f(x, y, z) =  М0(0, 1, 1).
М0(0, 1, 1).
| 2.30. f(x, y, z) =  М0(0,4,1). М0(0,4,1).
|
Задача 3. Найти полные дифференциалы указанных функций
| 3.1. z = 2x3y – 4xy5. | 3.2. z = x2ysinx – 3y. |
3.3. z = arctgx +  . .
| 3.4. z = arcsin(xy) – 3xy2. |
| 3.5. z = 5xy4 + 2х2y7. | 3.6. z = cos(x2 – y2) + x3. |
| 3.7. z = ln(3x2 - 2y2). | 3.8. z = 5xy2 – 3x3y4. |
| 3.9. z = arcsin(x+y). | 3.10. z = arctg(2x –y). |
3.11. z = 7x3y -  . .
| 3.12. z =  . .
|
3.13. z =  . .
| 3.14. z = cos(3x + y) – x2. |
| 3.15. z = tg((x + y)/(x - y)). | 3.16. z = сtg(y/x). |
| 3.17. z = xy4 – 3x2y+1. | 3.18. z = ln(x + xy – y2). |
| 3.19. z = 2x2y2 + x3 – y3. | 3.20. z =  . .
|
| 3.21. z = arcsin((x + y)/х). | 3.22. z = arctg(x - y). |
3.23. z =  . .
| 3.24. z = y2 - 3xy – x4. |
| 3.25. z = arccos(x + y). | 3.26. z = ln(y2 – x2 +3). |
| 3.27. z = 2 – x3 – y3 + 5х. | 3.28. z = 7х – x3y2 + y4. |
| 3.29. z = ey-x. | 3.30. z = arctg(2x - y). |
Задача 4. Вычислить значение производной сложной функции u = u(x, y), где x = x(t), y = y(t), при t = t0 с точностью до двух знаков после запятой
| 4.1. u = ex-2y, х = sint, y = t3, t0 = 0 | 4.2. u = ln(ex + e-y), х = t2, y = t3, t0 = -1. |
| 4.3. u = yx, х = ln(t-1), y = et/2, t0 = 2. | 4.4. u = ey-2x+2, х = sint, y = cost, t0 = p/2. |
| 4.5. u = x2ey, х = cost, y = sint, t0 = p. | 4.6. u = ln(eх + ey), х = t2, y = t3, t0 = 1. |
| 4.7. u = xy, х = et, y = lnt, t0 = 1. | 4.8. u = ey-2x, х = sint, y = t3, t0 = 0. |
| 4.9. u = x2e-y, х = sint, y = sin2t, t0 = p/2. | 4.10. u = ln(e-х + ey), х = t2, y = t3, t0 = -1. |
| 4.11. u = ey-2x-1, х = cost, y = sint, t0 = p/2. | 4.12. u = arcsin(x/y), х = sint, y = cost, t0 = p. |
| 4.13. u = arccos(2x/y), х = sint, y = cost, t0 = p. | 4.14. u = x2/(y+1), х = 1 - 2t, y = arctgt, t0 = 0. |
| 4.15. u = x/y, х = et, y = 2 – e2t, t0 = 0. | 4.16. u = ln(e-х + e-2y), х = t2, y = t3/3,t0 = 1. |
4.17. u =  , х = lnt, y = t2, t0 = 1. , х = lnt, y = t2, t0 = 1.
| 4.18. u=arcsin(x2/y), х = sint, y = cost,t0= p |
| 4.19 u = y2/х, x = 1-2t, y=1 + arctgt, t0= 0. | 4.20. u =  , x=sint, y = cost, t0 = , x=sint, y = cost, t0 =  . .
|
4.21. u = 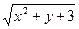 , х = lnt, y = t2, t0 = 1. , х = lnt, y = t2, t0 = 1.
| 4.22. u = 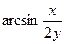 , x = sint, y=cost, t0 = p. , x = sint, y=cost, t0 = p.
|
4.23. u =  , x=sin2t, y = tg2 t, t0 = , x=sin2t, y = tg2 t, t0 =  . .
| 4.24. u =  , х = lnt, y = t2, t0 = 1. , х = lnt, y = t2, t0 = 1.
|
| 4.25. u = y/x, x = et, y = 1 – e2t, t0 = 0. | 4.26. u=arcsin(2x/y), х=sint, y=cost, t0 = p. |
| 4.27. u = ln(e2х + ey), х = t2, y = t4, t0 = 1. | 4.28. u=arctg(x+y), x=t2 + 2, y=4–t2, t0 = 1. |
4.29. u = 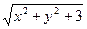 , х = lnt, y= t3, t0 = 1. , х = lnt, y= t3, t0 = 1.
| 4.30. u = arctg(xy), x = t + 3, y = et, t0 = 0. |
Задача 5. Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке М0(х0, у0, z0):
5.1. S: x2 + y2 + z2 +6z - 4x + 8 = 0, М0(2, 1, -1).
5.2. S: x2 + z2 – 4y2 = - 2xy, М0(-2, 1, 2).
5.3. S: x2 + y2 + z2 – xy + 3z = 7, М0(1, 2, 1).
5.4. S: x2 + y2 + z2 + 6y + 4z = 8, М0(-1, 1, 2).
5.5. S: 2x2 - y2 + z2 - 4z + y = 13, М0(2, 1, -1).
5.6. S: x2 + y2 + z2 - 6y + 4z +4= 0, М0(2, 1, -1).
5.7. S: x2 + z2 – 5yz + 3y = 46, М0(1, 2, -3).
5.8. S: x2 + y2 – xz - yz = 0, М0(0, 2, 2).
5.9. S: x2 + y2 + 2yz – z2 + y – 2z = 2, М0(1, 1, 1).
5.10. S: y2 – z2 + x2 – 2xz + 2x = z, М0(1, 1, 1).
5.11. S: z = x2 + y2 – 2xy + 2x - y, М0(-1, -1, -1).
5.12. S: z = y2 – x2 + 2xy - 3y, М0(1, -1, 1).
5.13. S: z = x2 - y2 – 2xy - x - 2y, М0(-1, 1, 1).
5.14. S: x2 -2y2 + z2 + xz – 4y = 13, М0(3, 1, 2).
5.15. S: 4y2 – z2 + 4xy – xz + 3z = 9, М0(1, -2, 1).
5.16. S: z = x2 + y2 – 3xy - x + y + 2, М0(2, 1, 0).
5.17. S: 2x2 - y2 + 2z2 + xy + xz = 3, М0(1, 2, 1).
5.18. S: x2 - y2 + z2 - 4x + 2y = 14, М0(3, 1, 4).
5.19. S: x2 + y2 - z2 + xz + 4y = 4, М0(1, 1, 2).
5.20. S: x2 - y2 - z2 + xz + 4x = -5, М0(-2, 1, 0).
5.21. S: x2 + y2 - xz + yz - 3x = 11, М0(1, 4, -1).
5.22. S: x2 + 2y2 + z2 - 4xz = 8, М0(0, 2, 0). 
5.23. S: x2 - y2 - 2z2 - 2y = 0, М0(-1, -1, 1).
5.24. S: x2 + y2 - 3z2 + xy = - 2z, М0(1, 0, 1).
5.25. S: 2x2 - y2 + z2 - 6x + 2y + 6 = 0, М0(1, -1, 1).
5.26. S: x2 + y2 - z2 + 6xy - z = 8, М0(1, 1, 0).
5.27. S: z = 2x2 - 3y2 + 4x - 2y + 10, М0(-1, 1, 3).
5.28. S: z = x2 + y2 - 4xy + 3x - 15, М0(-1, 3, 4).
5.29. S: z = x2 + 2y2 + 4xy – 5y - 10, М0(-7, 1, 8).
5.30. S: z = 2x2 - 3y2 + xy + 3x + 1, М0(1, -1, 2).
Задача 6. Найти вторые частные производные указанных функций. Убедиться в том, что  .
.
6.1. z =  . . 
| 6.2. z = ctg(x + y). |
| 6.3. z = tg(x/y). | 6.4. z = cos(xy2). |
| 6.5. z = sin(x2 - y). | 6.6. z = arctg(x + y). |
| 6.7. z = arcsin(x - y). | 6.8. z = arccos(2x + y). |
| 6.9. z = arctg(x - 3y). | 6.10. z = ln(3x2 - 2y2). |
6.11. z = 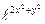 . .
| 6.12. z = ctg(y/x). |
6.13. z = tg  . .
| 6.14. z = cos(x2y2 –5). |
6.15. z = sin  . .
| 6.16. z = arcsin(x - 2y). |
| 6.17. z = arccos(4x - y). | 6.18. z = arctg(5x + 2y). |
| 6.19. z = arctg(2x - y). | 6.20. z = ln(4x2 - 5y3). |
6.21. z =  . .
| 6.22. z = arcsin(4x + y). |
| 6.23. z = arccos(x - 5y). | 6.24. z = sin  . .
|
| 6.25. z = cos(3x2 – y3). | 6.26. z = arctg(3x + 2y). |
| 6.27. z = ln(5x2 - 3y4). | 6.28. z = arcctg(x - 4y). |
| 6.29. z = ln(3xy - 4). | 6.30. z = tg(xy2). |
Задача 7. Исследовать на экстремумы следующие функции
| 7.1. z = x2-2y²-x+14y |  7.2. z= x³+8y³-6xy+5. 7.2. z= x³+8y³-6xy+5.
|
| 7.3. z = 1+15 x -2x²- xy -2y². | 7.4. z = 1+6 x -x²- xy - y². |
| 7.5. z = x³+y²-6xy-39х +18у+20. | 7.6. z = 2x³+2y³-6xy +5. |
| 7.7. z = 3x³+3y³-9xy +10. | 7.8. z = x² + xy +y² +х – у+1. |
| 7.9. z = 4 (x –y)- x² - y². | 7.10. z = 6 (x –y)-3x² - 3y². |
| 7.11. z = x² + xy +y² - 6х – 9у. | 7.12. z = (x – 2)² + 2y² - 10. |
| 7.13. z = (x – 5)² + y² + 1. | 7.14. z = x³ + y³ - 3xy. |
7.15. z = 2xy - 2x² - 4y². 
| 7.16. z = х√у - х²- y +6х +3. |
| 7.17. z = 2xу - 5x² - 3y² +2m. | 7.18. z = xy (12 - x – y). |
| 7.19. z = xу - x² - y² +9. | 7.20. z = 2xу - 3x² - 2y² + 10. |
7.21. z = x³ + 8y³ - 6xy + 1. 
| 7.22. z = у√х - у²- х - 6у. |
| 7.23. z = x² - xy +y² + 9х + 6у +20. | 7.24. z = ху (6 - х – у). |
| 7.25. z = x² + y² - ху + х + у. | 7.26. z = x² + xy +y² - 2х - у. |
| 7.27. z = (x – 1)² + 2y². | 7.28. z = ху - 3x² - 2y². |
| 7.29. z = x² + 3 (у +2)². | 7.30. z = 2 (х + у) -x² - y². |
Список литературы
Дата добавления: 2015-09-03; просмотров: 165 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сопоставление полученных результатов с требуемыми показателями | | | В А Р И А Н Т 4 |