Метод неполной взаимозаменяемости

Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих

звеньев.

Сборка осуществляется без пригонки, регулировки и подбора звеньев.

Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер, и вероятность того, что все звенья с самыми небла­гоприятными сочетаниями окажутся в одном изделии, весьма мала.

Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных со­четаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допусков. При этом расши­ряются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовле­ния деталей.

Задачей расчета является назначение допусков на составляющие звенья, соответствующих оди­наковой степени точности.

Учитывая случайный характер сочетаний действительных размеров деталей в изделии, восполь­зуемся уравнением для определения дисперсии суммы независимых случайных величин:

Допустим, что погрешность всех звеньев изменяется по закону нормального распределения, а границы рассеяния размеров для составляющих звеньев 6σ совпадают с границами полей до­пусков, тогда:

Для замыкающего звена допустим, что:

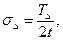
где t — коэффициент риска.

Тогда:

Обозначим через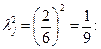

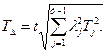(4.8)

Формула (4.8) устанавливает связь между допуском на замыкающий размер и допусками на со­ставляющие звенья.

Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, восполь­зуемся известной формулой T_j= k_j i_j и подставим ее в выражение (4.8). Потребуем, чтобы k у всех звеньев были одинаковыми, тогда:

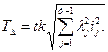
Окончательно получим:

(4.9)

Значение k характеризует точность, с которой следует изготовить все составляющие звенья размерной цепи при заданных условиях.

При обработке деталей разброс размеров у них может распределяться и не по закону Гаусса. В этом случае можно также воспользоваться формулой (4.9), только при этом следует поставить другие значения .

Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то =

При неизвестном характере рассеяния размеров рекомендуется принимать закон равной вероятности с =

На основании предельных теорем теории вероятностей независимо от характера рассеяния размеров составляющих звеньев разброс размеров замыкающего звена размерной цепи будет близок к закону нормального распределения.

В зависимости от принятого процента риска Р значения t выбирают из ряда, приведенного в табл. 4.4.

Таблица 4.4

Р, %	32.00	10.00	4.50	1.00	0.27	0.10	0.01
t	1.00	1.65	2.00	2.57	3.00	3.29	3.89

Пример

Вероятностный метод расчета рассмотрим на том же узле (см. рис. П.8.2). По техническим требо­ваниям необходимо обеспечить осевой зазор A_Δ=0.2^+0.25. Требуется назначить допуски и откло­нения на составляющие звенья при Р= 0.27% и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).

Дата добавления: 2015-09-03