Этапы формирования вычислительных навыков

ПРЕПОДАВАНИЯ МАТЕМАТИКИ

Тема10. Формирование вычислительных навыков

Требования к знаниям и умениям студентов

Студенты должны знать:

- содержание и особенности построения курса математики;

- основные подходы обучения и развития младших школьников в математической деятельности;

- оснащение учебного процесса в начальной школе.

Студенты должны уметь:

- анализировать содержание темы;

- разрабатывать соответствующие теме дидактические упражнения, подбирать дидактические игры;

- предвидеть возможные ошибки и затруднения младших школьников;

- осуществлять усвоение школьниками таблиц сложения, вычитания, умножения, деления;

- формировать вычислительные навыки устных и письменных вычислений;

- диагностировать уровень сформировавшихся вычислений каждого школьника.

План

1. Характеристика вычислительных навыков

2. Этапы формирования вычислительных навыков.

3. Формирование вычислительных навыков на основе организации повторения.

4. Анализ качества устных вычислительных навыков учащихся начальных классов.

Литература

Основная литература

1. Белошистая, А.В. Методика обучения математике в начальной школе: Курс лекций: учеб. пособие для студентов высш. пед. учеб заведений [Текст] / А.В. Белошистая. - М.: Гуманитар. изд. центр ВЛАДОС, 2005. – 455 с.: ил. – 5000 экз. – ISBN 5-691-01422-6. – С. 5 – 26.

2. Зайцева, С. А. Методика обучения математике в начальной школе [Текст] / С.А. Зайцева, И.Б. Румянцева, И.И. Целищева. – М.- Гуманитар. изд.

3. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] / Н.Б. Истомина. - М., Академия; 1999. – 285 с. – 5000экз.- ISBN – 5-7695-0310-6. – С. 7 – 12.

4. Истомина, Н.Б. Преемственность при изучении чисел в начальной и основной школе [Текст] / Н.Б. Истомина, Г.В. Вонтелева. - М.: Московский психолого-социальный институт, 2003. – 144 с. – ISBN 5-89502-358 -4.

Дополнительная литература

1. Артемов А.К. Образцы действий в обучении математике // Начальная школа. 1989. №2.

2. Бантова Л.А. Система формирования вычислительных навыков // Начальная школа. 1993. №11.

3. Бантова Л.А. Ошибки учащихся в вычислениях и их предупреждение // Начальная школа. 1982. №8

4. Белошистая А.В.Прием формирования устных вычислительных умений в пределах 100 // Начальная школа. 2001. №7.

5. Бельтюкова Г.В. Методические ошибки при формировании у школьников вычислительных навыков // Начальная школа. 1980. №8.

6. Бростак Г.Д. Использование занимательного материала на уроках математики // Начальная школа. 1989. №1.

7. Земцова Л.И., Сушкова Е.Ю. Роль дидактической игры на уроке математики // Начальная школа. 1988. №10.

8. Истомина Н.Б., Шмырева Г.Г. Формирование навыков сложения и вычитания в пределах 10 // Начальная школа. 1987. №10.

9. Попова С.В. Мой взгляд на современный урок // Начальная школа. 2001. №4.

10. Петрова И.А. Использование игры в учебном процессе // Начальная школа. 1988. №3.

11. Радюкова Л.А. Из опыта обучения математике в 1-2 классах четырехлетней школы // Начальная школа.1995. №7.

12. Липатникова И.Г.Роль устных упражнений на уроках математики // Начальная школа. 1998. №2.

13. Мозжорина Т.И. Уроки изучения нового материала по математике // Начальная школа. 2001. №4.

14. Петерсон Л.Т. Активизация деятельности детей при изучении вычитания двузначных чисел с переходом через разряд // Начальная школа. 1997. №6.

15. Полозова Т.П. Роль самоконтроля в формировании вычислительных навыков // Начальная школа. 1985. №3.

16. Фонин Д.С., Целищева И.И. Организация повторения на уроках математики при ознакомлении с новыми вычислительными приемами // Начальная школа. 1989. №2.

Контрольные вопросы

3.1. Сформулируйте понятие навыка.

3.2. Дайте характеристику вычислительному приему.

3.3. Дайте определение вычислительному навыку.

3.4. Назовите качества, которыми характеризуется вычислительный навык.

3.5. Как формируется вычислительный навык?

3.6. Назовите этапы формирования вычислительного навыка.

3.7. Какие нормы проверки вычислительного навыка Вы знаете?

Краткое содержание вопросов плана

4.1. Характеристика вычислительных навыков

Российские выпускники школ издавна славились умением быстро и точно выполнять в уме множество арифметических действий над числами. В настоящее время этот вычислительный навык несколько утратился. Это, возможно, объясняется внедрением в процесс обучения альтернативных систем, где в объяснительных записках данный вопрос не оговаривается.

Исходя из того, что вычислительный навык - это высокая степень овладения вычислительными приемами, можно сделать вывод, что приобрести вычислительные навыки - это значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнить необходимые операции достаточно быстро. Полный вычислителей навык характеризуется следующими качествами: правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом, точностью и скоростью.

Необходимо заметить, что формирование вычислительного навыка, обладающего названными качествами, обеспечивается построением начального курса математики и использованием соответствующих вычислительных приемов.

Прием вычисления над данными числами складывается из ряда последовательных операций (системы операций), выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами. Причем выбор операций в каждом приеме определяется теми арифметическими положениями, которые используются в качестве его теоретической основы.

Дадим характеристику выделенных качеств на основе материала из методических работ М.А. Бантовой.

Правильность: ученик правильно находит результат арифметического действия над данными числами, т.е. правильно выбирает и выполняет операции, составляющие прием.

Осознанность: ученик понимает, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это служит доказательством того, что правильно определена система операций. Осознанность проявляется в том, что ученик может объяснить, как он решал пример и почему можно так решать.

Рациональность: ученик, сообразуясь с определенными условиями, находит для конкретной ситуации более рациональный прием, т.е. выбирает из возможных операций те, выполнение которых легче и быстрее других приводит к результату арифметического действия. Естественно, что данное качество может проявляться тогда, когда для данного случая существуют разные пути нахождения результата, и ученик, используя различные знания, может вспомнить несколько приемов и выбрать наиболее рациональный. Как видим, рациональность непосредственно связана с осознанностью навыка.

Обобщенность: ученик может применить прием вычисления к большому числу случаев, способен перенести его на новые задания. Обобщенность, так же как и рациональность, теснейшим образом связана с осознанностью, так как единым для различных случаев вычисления будет прием, основа которого - одни и те же теоретические положения.

Автоматизм (свернутость): ученик выделяет и выполняет операции быстро и в свернутом виде, но всегда может вернуться к объяснению их выбора.

Программа по математике для начальной школы предусматривает разную степень автоматизации выполнения арифметических действий. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям (5 + 3, 8 - 5, 9 + 6, 15 - 9,

7 - 6, 42: 6). Здесь необходим уровень, при котором ученик сразу же соотносит с двумя данными числами третье число (результат арифметического действия), не выполняя отдельных операций. По отношению к другим случаям происходит частичная автоматизация вычислительных навыков: ученик предельно быстро выделяет и выполняет систему операций, не объясняя, почему выбрал именно их и как выполнял каждую.

Следует отметить, что осознанность и автоматизм не являются противоречивыми качествами. Они всегда выступают в единстве: при свернутом выполнении операций осознанность сохраняется, но обоснование системы действий происходит в плане внутренней речи. Благодаря этому учащийся может в любой момент дать развернутое объяснение своего выбора.

Прочность: ученик правильно использует сформированные вычислительные навыки через длительное время.

В целях формирования осознанных, обобщенных и рациональных навыков начальный курс математики строится так, что изучение того или иного вычислительного приема происходит после того, как учащиеся усвоят материал, являющийся его теоретической основой. Например, сначала изучается распределительный закон умножения, а затем прием внетабличного умножения.

Теоретической основой вычислительных приемов служат определения арифметических действий, их свойства и следствия, вытекающие из них. В связи с этим С.А. Зайцева, И.Б. Румянцева, И.И. Целищева выделяют группы приемов, имеющие общую теоретическую основу, предусмотренную действующей программой по математике для начальных классов.

1. Приемы, теоретической основой которых является конкретный смысл арифметических действий:

- приемы сложения и вычитания чисел в пределах 10 для случаев вида: а ± 2, а ± 3, а ± 4, а + 0;

- прием нахождения табличных результатов умножения;

- прием нахождения табличных результатов деления (только на начальной стадии) и деления с остатком;

- приемы умножения на единицу и нуль.

Все они вводятся сразу после ознакомления учащихся с конкретным смыслом арифметических действий и готовят к усвоению их свойств. Хотя в основе некоторых из названных приемов лежат признаки арифметических действий (так, прибавление двух по единице выполняется на основе использования свойства прибавления суммы к числу), эта основа учащимся не раскрывается. Перечисленные приемы базируются на выполнении операций над множествами.

2. Приемы, теоретической основой которых служат свойства арифметических действий. К этой группе относится большинство вычислительных приемов:

- сложение и вычитание для случаев вида 2 + 8, 54 ± 20, 27 ± 3, 40 - 6, 9 + 3, 12 - 3,

45 ± 7, 50 ± 23, 67 ± 32, 74 + 18;

- сложение и вычитание чисел больших, чем 100;

- письменное сложение и вычитание;

- умножение и деление для заданий типа: 14 - 5, 15 - 14, 81: 3, 18 - 40, 180: 20;

- умножение или деление для чисел, больше 100,

- письменное умножение и деление.

Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, затем - приемы вычислений.

3. Приемы, теоретической основой которых являются связи между компонентами и результатами арифметических действий. К ним относятся приемы для случаев вида 9 - 7, 21: 3, 60: 20, 54: 18, 9: 1, 0: 6. При их введении сначала рассматриваются связи между компонентами и результатами действий сложения или умножения, а затем - вычислительный прием.

4. Приемы, теоретической основой которых является изменение результатов арифметических действий в зависимости от изменения одного из компонентов. Это округление при выполнении сложения и вычитания чисел (46 + 19, 512 - 298) и умножение и деление на 5, 25, 50. Их введение требует предварительного изучения соответствующих зависимостей.

5. Приемы, теоретической основой которых являются вопросы нумерации чисел. Это приемы для случаев вида 0 + 1, 10 + 6, 6 + 10, 16 - 10, 16 - 6, 57 - 10, 1200: 100, а также аналогичные для больших чисел. Изучение данных приемов предусматривается после усвоения вопросов нумерации.

6. Приемы, теоретическая основа которых - правила. К ним относятся приемы для двух случаев: а • 1 и а • 0. Поскольку правила умножения чисел на единицу и нуль есть следствия из определения действия умножения целых неотрицательных чисел, то они просто сообщаются учащимся и в соответствии с ними выполняются вычисления.

Этапы формирования вычислительных навыков

Формирование любого вычислительного навыка проходит одни и те же этапы (см. таблицу).

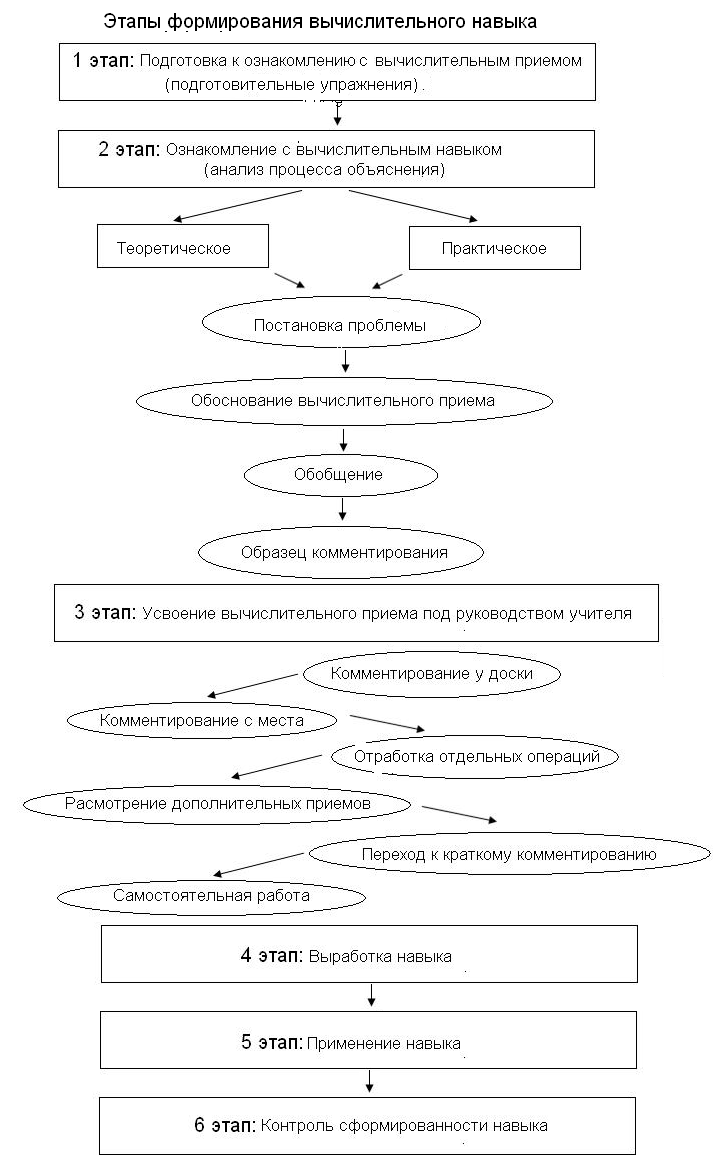
Дадим характеристику каждому из названных этапов.

1. Подготовка к введению нового приема. Целью этого первого этапа является обеспечение учащихся необходимыми условиями для успешного понимания и усвоения нового вычислительного приема.

На уроке, где дается новый вычислительный прием, этот этап обязателен, на предшествующих уроках подготовка к его изучению включается в систему подготовительных упражнений.

На этом этапе обеспечивается готовность к усвоению вычислительного приема. Учащиеся должны понять те теоретические положения, на которых основывается вычислительный прием, а также овладеть каждой операцией, составляющей его. Чтобы обеспечить соответствующую подготовку, надо проанализировать прием и установить, какими знаниями должен овладеть ученик, и какие вычислительные» навыки он уже приобрел. Например, можно считать, что учащиеся подготовлены к ознакомлению с вычислительными приемами для случаев в ± 2, если они знают конкретный смысл действий сложения и вычитания, состав числа 2 и владеют вычислительными навыками сложения и вычитания для случаев вида а ± 1. Показателем готовности к введению приема внетабличного умножения (14 • 5) будет:

- знание правила умножения суммы на число,

- знание десятичного состава чисел в пределах 100,

- овладение навыками табличного умножения,

- умножение числа 10 на однозначные числа,

- сложение двузначных чисел.

Центральное звено в процессе подготовки к новому приему - овладение учеником основными операциями, которые составят этот прием. Поэтому очень важно продумать содержание системы подготовительных упражнений.

К одним и тем же вычислительным случаям можно применять различные вычислительные приемы.

Например, объясняя вычитание типа 12 – 5, чтобы правильно составить подготовительные упражнения, рассматриваем первый прием для вычисления примеров данного типа: необходимо вычесть столько, чтобы получилось 10. 12 – 5 = 12 - (2 + 3) = 10 – 3 = 7. анализируя этот прием, мы:

1) в начале догадались, что чтобы получить число 10, нужно от 12 - 2, т.к. от 10 потом легко отнимать;

2) затем мы разложили 5 = 2 +?, ищем второе число;

3) 10 – 3 = 7.

Пришлось выполнить 3 операции, значит, необходимо составить систему заданий к каждой из названных операций.

Для первой операции: на доске записываем числа 15, 14, 18, 16, 13. учащимся задаем вопрос: «Какое число нужно вычесть из каждого из представленных чисел, чтобы получилось 10?»

Для второй операции: разложить число так, чтобы одно из слагаемых было 3.

8 = 3 +?, 7 = 3 +? и т.д.

Для третьей операции предложить примеры 10 - а. Необходимо так организовать работу, чтобы на уроке спросить разных учеников с большой скоростью.

Рассмотрим второй прием: здесь детям следует знать состав числа 12, затем, на основе знания связи сложения и вычитания, делаем вывод, что 12 – 5 = 7.

Покажем этот прием подробнее. Данное число нужно разложить на сумму чисел так, чтобы одно из слагаемых было 5. Из того, что 5 + 7 = 12, следует, что 12 – 5 = 7, и 12 – 7 = 5, то есть к одному примеру на сложение можно составить два примера на вычитание.

Составим систему упражнений:

- 12 это 5 и сколько? (6 – 7 подобных примеров);

- на доске записано: 6 + 7 = 13, 5 + 8 = 13, 4 + 7 = 11. Задание: «К каждому из этих примеров записать по два соответствующих примера на вычитание».

Итак, мы проанализировали прием и составили необходимые подготовительные упражнения.

Формы проведения подготовительных упражнений могут быть самыми разнообразными, т.к. все вычислительные навыки, все знания, которые нужны для конкретного приема, должны быть хорошо отработаны. Необходимо, чтобы за короткий промежуток времени в работу был вовлечен максимум учащихся, и было выполнено достаточное количество упражнений.

Недостатки, встречающиеся при подготовке системы дополнительных упражнений:

1) система подготовительных упражнений бывает неполная не все необходимые типы упражнений представлены на уроке;

2) формулировки упражнений не всегда соответствуют операции, предложенной в приеме.

Поэтому учитель должен провести анализ процесса объяснения.

Допустим, что нам надо объяснить прием 12 · 3. Отметим, что обоснование в начальных классах можно давать практическое и теоретическое. Теоретическое обоснование: 12 · 3 = (10 + 2) · 3. Учащиеся уже могут выполнять эти действия, так как знакомы с правилом умножения суммы на число. Перед тем, как приступить к работе с аналогичными примерами, они должны это правило вспомнить. Таким образом, в системе подготовительных упражнений необходимо повторить это правило, для этого детям предлагаем 3 - 4 упражнения, чтобы можно было спросить несколько человек. Проведем анализ этого вычислительного приема.

- Разложить двузначное число на сумму разрядных слагаемых.

- Умножить десятки на число.

- Табличное умножение (однозначное число на однозначное число).

- Сложение десятков с однозначным числом.

Таким образом, для этого вычислительного прима нужно 4 типа подготовительных упражнений.

Для известного нам уже примера 12 - 5 теоретической основой является правило вычитания суммы из числа: чтобы вычесть сумму из числа, можно вычесть из этого числа любое слагаемое, а затем из полученного результата вычесть другое слагаемое. Получаем

12 – 5 = 12 - (2 + 3) = 12 - 2- 3 = 10 – 3 = 7. Здесь нужно выполнить три типа упражнений.

2. Ознакомление с вычислительным приемом. Второй этап представляет собой стандартную схему объяснения, которую можно разделить на четыре шага.

Первый шаг – объяснение начинается спостановки проблемы, которую можно осуществить по-разному:

а) учитель может начать так: «Сегодня мы познакомимся...»;

б) учитель напоминает о том, что уже изучено, а затем переходит к объяснению нового материала со словами: «Сегодня мы попробуем умножать числа, когда первый множитель двузначное число», - затем идет объяснение;

в) учитель говорит о том, что умеют дети, потом обращается к ним так с вопросом: «Кто из вас сможет умножить 12 · 3 =?»; г) «Ребята, попробуем умножить «старым» способом 12 · 3 = 12 + 12+ 12 = 36. Как вы поступите, если нужно 12 · 9? Вам придется очень долго считать. Мы сегодня познакомимся с новым более коротким способом умножения».

Второй шаг - обоснование вычислительного приема. Оно может проходить по-разному:

- обоснование вычислительного приема проводит сам учитель. Обычно это сводится или к выполнению практических действий с предметами или происходит опора на какой-либо теоретический факт. Например, необходимо объяснить, как вычислить 24 + 20. Для этого берутся полоски с кружками (на каждой полоске по 10 кружков). Учитель обращает внимание детей на то, что удобнее сложить одинаковые полоски (т.е. десятки с десятками), а затем складывать десятки с единицами;

- если же опору сделать на теорию, то 24 + 20 = (20 + 4) + 20 = <удобнее> =

(20 + 20) + 4 = 40 + 4 = 44.

Таким образом, в основе теоретической и в обосновании практических действий рассматриваются одни и те же свойства арифметических действий, только при выполнении практических действий они используются в неявном виде (на интуитивном уровне), а при опоре на теоретический факт свойства используются в явном виде. Иногда можно и полезно проводить обоснование вычислительного приема с практическими действиями и теоретическими фактами.

При объяснении вычислительного приема учитель привлекает детей. Но более целесообразно проводить объяснения от начала, до конца не прерывая его, так как в беседе дети могут не уловить сути.

Если в обоснование вычислительного приема вовлекаются все учащиеся, тогда выполнение практических действий выполняется на партах каждым школьником. Если же основой является теоретический факт, то учащиеся в тетрадях выполняют развернутые записи. Но, нужно помнить, что не стоит соединять предметные действия на доске с предметными действиями за партой, так как у детей «рассеивается» внимание.

Обоснование вычислительного приема может осуществляться с помощью учебника, под руководством учителя или самостоятельно.

Третий шаг - он посвящен обобщению. Здесь происходит подробное проговаривание смысла вычислительного приема. Например, после того, как рассмотренные примеры 24 + 20, 56 + 30, 78 + 10, нужно обобщить, что десятки легче складывать с десятками. Мы все это заметили. Здесь полезно использовать различные опорные схемы, например.

1) пишу;

2) вычитаю единицы из единиц, десятки из десятков;

3) разность...

Опорная схема показывается учащимся класса, проговариваются объяснения и на глазах детей эта схема вывешишается у доски. Висит она до тех пор, пока идет изучение вычислительного приема.

Четвертый шаг - образец комментирования. Учитель говорит: «Ребята, послушайте, как вы должны объяснить:...».

На этом этапе ученики осваивают вычислительный прием: какие операции надо выполнять, в каком порядке, почему именно так можно найти результат арифметического действия.

При введении большинства вычислительных приемов целесообразно использовать наглядность. Для приемов первой группы - оперирование множествами. Например, прибавляя к 7 число 2. придвигаем к 7 квадратам (кружкам и т.п.) 2 квадрата (кружка и т.п.) по одному. В ходе работы над приемами второй группы в качестве наглядности используется развернутая запись всех операций. Например, при введении приема внетабличного умножения выполняется такая запись: 14 • 5 = (10 + 4) • 5 = 10 • 5 + 4 • 5 = 70. В ряде случаев наряду с ней используется и оперирование множествами (например, при ознакомлении с приемами сложения и вычитания в пределах 100). Выполнение каждой операции важно сопровождать устными пояснениями. Сначала они производятся под руководством учителя, а затем учащиеся делают это самостоятельно. В пояснении указывается, какие необходимы операции, каков их порядок; называется результат каждой из них. При этом не раскрываются ранее изученные приемы, входящие в качестве операции в новом приеме (основные операции). Например, прибавляя к 7 число 2, ученик так поясняет выполнение операций: «К семи прибавлю 1, получится 8; к 8 прибавлю 1, получится 9» (как прибавить 1 - не поясняется). При умножении чисел 14 и 5 пояснение будет следующим: заменю число 14 суммой разрядных слагаемых 10 и 4, получу пример: сумму чисел 10 и 4 умножить на 5. Умножим на 5 первое слагаемое - 10, получится 50, умножим на 5 второе слагаемое - 4, получится 20, сложим результаты 50 и 20, получится 70 (здесь не поясняется, как умножить 10 на 5, как умножить 4 на 5 и как сложить 50 и 20). Комментарий к выбору и выполнению операций приводит к пониманию сущности каждого шага и всего приема в целом, что в дальнейшем будет основой осознанных вычислительных навыков.

Степень самостоятельности учащихся должна возрастать при переходе от приема к приему одной группы. Следует учитывать, что во многих случаях ученики могут без помощи учителя найти новый вычислительный прием и дать соответствующее обоснование. Например, установлено, что все приемы устных вычислений над числами в пределах 1000 учащиеся находят сами, поскольку они являются прямым аналогом приемов, изученных в концентре «Сотня» (сравнить: 94 + 7 и 90 + 70, 8 • 4 и 80 • 4 и т.п.). Значительно повышается уровень самостоятельности школьников в «открытии» новых приемов, если используются «предписания - планы» (Л.Н. Ланда). Например, при изучении сложения и вычитания в пределах 100 учащимся можно предложить руководствоваться при вычислении такой последовательностью: заменить одно из чисел суммой удобных слагаемых (часто удобными являются разрядные слагаемые), назвать, какой получился пример, и решить его оптимальным способом. Умение пользоваться планом способствует нахождению учащимися различных вычислительных приемов для новых случаев, что является предпосылкой образования рациональных навыков и вместе с тем формирования осознанности и обобщенности вычислительного навыка.

3 Третий этап - усвоение вычислительного приема можно разбить на шесть шагов.

Первый шаг - комментирование у доски. Здесь учитель должен добиться того, чтобы большинство учащихся класса проговорили комментирование. Вначале слово дается «сильным» детям. К доске, где каждый комментирует и пишет, можно вызвать 3 - 4 учащихся, а остальные школьники в это время пишут у себя в тетрадях.

Второй шаг - комментирование с места. На эту работу достаточно трех, четырех примеров. Один учащийся комментирует с места, а остальные пишут в своих тетрадях.

В некоторых вычислительных приемах есть трудные моменты, из-за которых учащиеся не могут решить пример. Поэтому необходим третий шаг, где происходит отработка учащимися отдельных операций приема. Например, когда изучается умножение со вторым множителем, в середине которого стоит нуль, то выясняется, под какой цифрой следует начать записывать второе неполное произведение.

Четвертый шаг - рассмотрение дополнительных к основному вычислительных приемов. Например, 72: 18 - здесь основной вычислительный прием – это прием подбора («Мы должны подобрать такое число, которое при умножении на 18 дает 72. 2 · 18 = 36, проверим: 36 # 72. 3 · 18 = 54, проверим: 54 # 72. 4 · 18 = 72, проверим: 72 = 72, значит 72: 18 = 1»). После того, как изучаемый прием объяснен, проговорен, учитель может показать, что можно воспользоваться другим приемом. Для этого нужно посмотреть на последние цифры в числах 72 и 18, а затем вспомнить из таблицы умножения числа, которые заканчиваются на 2 и делятся на 8: это число 32. 32:8 = 4 и 72:18 = 4. Проверим: 4 · 18 = 72. Этот способ короче! Приведем еще один прием: 66: 11 - здесь можно просто догадаться (способ догадки), а потом проверить.

Пятый шаг - переход от подробного комментирования к краткому комментированию, вначале для «сильных» детей, а потом уже и для всех учащихся класса. Здесь происходит закрепление знания приема.

Вычислительное умение – это развернутое осуществление действия, в котором каждая операция осознается и контролируется.

Вычислительный навык – это высокая степень овладения вычислительными приемами. Приобрести вычислительные навыки – это значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнить эти операции достаточно быстро, с пропуском промежуточных операций, когда контроль переносится на конечный результат.

На этом этапе учителю важно предусмотреть ряд стадий становления у детей вычислительных навыков.

На первой стадии закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие его, комментируя каждое действие вслух и одновременно производя развернутую запись, если она была предусмотрена на предыдущем этапе. Таким образом, ученики выполняют самостоятельно то, что на предыдущем этапе делали под руководством учителя. Подробное объяснение и развернутая запись позволяют им осознанно усвоить вычислительный прием. Начинается эта стадия, как правило, на том же уроке, на котором учитель знакомит детей с новым приемом. Заметим, что не следует слишком долго задерживаться на этой стадии, так как школьники настолько привыкают к подробной записи и подробному объяснению, что всегда пользуются ими, а это сдерживает свертывание операций.

На второй стадии происходит частичное свертывание выполнения операций: учащиеся про себя выделяют их, обосновывают выбор и порядок работы, вслух же проговаривают выполнение основных действий, т.е. промежуточных вычислений. Надо специально учить детей выделять основные операции в каждом вычислительном приеме. Так, при формировании навыка внетабличного умножения учитель на этой стадии просит, чтобы при умножении, например, 28 на 3 учащиеся про себя заменили число суммой разрядных слагаемых (20 и 8). Мысленно представим пример (сумму чисел 20 и 8 умножить на 3), а вслух объяснили, как удобнее его решить, называя только, над какими числами и какие арифметические действия они выполняют. Например, 20 умножить на 3, получится 60; 8 умножить на 3, получится 24, к 60 прибавить 24, получится 84. Развернутая запись при этом не делается. Сначала комментарий ведется под руководством учителя, а затем самостоятельно. Проговаривание вслух помогает выделить и подчеркнуть основные операции, а выполнение про себя вспомогательных действий способствует их свертыванию.

На третьей стадии происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все действия, т.е. происходит свертывание основных операций. Чтобы добиться этого, надо и на данной стадии руководить деятельностью учащихся: учитель предлагает детям выполнять про себя и промежуточные вычисления (основные операции), а называть или записывать только окончательный результат. Свертывание основных операций будет несколько отставать от свертывания вспомогательных (их свертывание началось на предыдущей стадии), благодаря чему основные операции будут актуализироваться: ученики воспроизведут именно те действия, выполнение которых позволит им правильно и быстро найти результат. Акцентуация основных операций и выполнение их в свернутом плане и есть собственно вычислительный навык.

На четвертой стадии наступает предельное свертывание выполнения операций: учащиеся производят все действия в свернутом виде, предельно быстро, т.е. овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений.

На всех стадиях формирования вычислительного навыка решающую роль играют упражнения на применение вычислительных приемов, причем содержание заданий должно подчиняться целям, которые ставятся на соответствующих стадиях. Важно, чтобы:

- было достаточное число упражнений при отработке вычислительного навыка;

- они были разнообразными как по числовым данным, так и по форме;

- в заданиях предусматривались аналогии и предлагались упражнения на сравнение приемов, сходных в том или ином отношении.

Названные стадии не имеют четких границ: одна постепенно переходит в другую. Надо иметь в виду, что свертывание выполнения операций не у всех учащихся происходит одновременно, поэтому важно время от времени возвращаться к полному объяснению и развернутой записи. Продолжительность каждой стадии определяется сложностью приема, подготовленностью учащихся и поставленными целями.

Шестой шаг - это самостоятельная работа, целью которой является проверка усвоения учащимися класса нового вычислительного приема. Эта цель говорит об особенностях самостоятельной работы, которая не проводится по вариантам. В эту работу не нужно включать много заданий.

После выполнения проводится обязательная проверка каждой работы с последующим пояснением.

На четвертом этапе - происходит выработка навыка табличных устных и письменных вычислений. Он вырабатывается в процессе тренировочных упражнений. В табличных вычислениях очень много внимания уделяется скорости, а в устных и письменных приемах вырабатывается беглое вычисление. Здесь можно говорить о качествах, характеризующих навык. Основные из них - это безошибочность, быстрота и прочность.

Безошибочность – это выявление у каждого конкретного ученика ошибки и ее исправления.

Быстрота проверяется на вычислениях с ограничением времени их выполнения.

Прочность можно проверить так:

1) контроль сформированности навыка через длительное время;

2) применение навыка в новых или усложненных условиях.

Пятый этап - применение навыка. Здесь показывается, в каких ситуациях могут быть применены полученные навыки и одновременно продолжаются обрабатываться названные основные качества навыка.

Контроль сформированности навыка (как мы заметили) осуществляется на третьем этапе - этап усвоения вычислительного приема. Этот контроль является текущим.

На шестом этапе - (этапе контроля) осуществляется итоговая проверка сформированности навыка. Одна их ведущих задач – формирование вычислительных навыков быстрых и осознанных. Нужно заметить, что формы проверки зависят от того, какой навык проверяется.

В методике преподавания математики выделены следующие группы вычислений:

1 группа – навыки табличных вычислений, которые должны быть доведены до автоматизма;

2 группа – навыки устных вычислений. Это те вычисления, которые выполняются с помощью специальных приемов устных вычислений. Например: 25+37 можно воспользоваться таким приемом (20 + 5) + (30 + 7) = (20 + 30) + (5 + 7) = 50 + 12 = 62.

3 группа – навыки письменных вычислений. Результат этих вычислений находится с помощью специальных приемов для письменных вычислений (см. таблицу).

Устные вычисления	Письменные вычисления
1) вычисления или не записываются, или запись вычисления производится в строчку;	1) по форме записи: в столбик.
2) здесь правил нет, можно использовать разные способы, например: 25 + 7 = (25+ 5)+ 2 =...;	2) устанавливается специальный алгоритм вычислений (система правил, которые выполняются в определенной последовательности). Все мыслят одинаково, по алгоритму!
3) действие начинает выполняться со старших разрядов (48: 4 =40: 4 + 8: 4 = 10 + 2 = 12).	3)действие, как правило, начинается с единиц (за исключением деления).

Навыки табличных вычислений формируются с изучением приемов, т.е. формирование каждого навыка, в том числе и табличного, начинается с формирования вычислительного приема.

.В начальном курсе математики учащиеся должны усвоить на уровне навыка:

- таблицу сложения и вычитания в пределах 10;

- таблицу сложения однозначных чисел с переходом через десяток и соответствующие случаи вычитания;

- таблицу умножения и соответствующие случаи деления.

Если изучается таблица, то учитель должен проверить знания каждого случая таблицы у каждого ученика. Замечено, что если ученик знает таблицу наизусть, то даже при плохой реакции он ответ дает через три секунды. Знание табличных вычислений всех учеников в классе учитель обычно проверяет с помощью перфокарт. Ученик должен написать ответ к 15 примерам за 3 минуты (это рассчитано на самого слабого ученика).

Достичь максимального охвата учеников при проверке возможно, если учитель использует перфокарты.

При проверке сформированности навыков устных и письменных вычислений достаточно рассмотреть лишь несколько типичных примеров. Ученику на каждый нетабличный проверяемый вычислительный случай дается минимум два примера. Например, проверка вычислительного навыка для случая деления на двузначное число:

1) 4316│52 (2примера) 2) 573│35 (2 примера)
0 │83 13 │16

3) 7368│24 (2 примера) 4) 31050│ 45 (2 примера)
0 │307 0 │690

Ограничение времени происходит условно. Специальных норм нет. Главное, чтобы ученик выполнил верно, все примеры.

Таким образом, этапы формирования вычислительного навыка для всех вычислительных случаев одинаковы, разница при формировании табличного навыка и навыков устных и письменных вычислений заключается в конечном результате.

На схеме показаны этапы формирования вычислительного навыка.

Дата добавления: 2015-09-03