
|
Читайте также: |
Задачи с параметром
1) При каких значениях параметра a уравнение (a2-4)x=a2+a-6
· Имеет бесконечно много решений?
· Не имеет решений?
· Имеет единственное решение?
2) При каких значениях параметра a неравенство xa2<a+x
· Не имеет решений?
· Выполняется для любых x?
3) При каких значениях параметра a система a + y - 0,5a2x = 0
8x – y + 4 = 0
· Имеет бесконечно много решений?
· Не имеет решений?
· Имеет единственное решение?
4) При каких значениях параметра b уравнение (2b-5)x2-2(b-1)x+3=0
· Имеет единственное решение?
· Имеет два различных корня?
5) При каких значениях параметра b уравнение x2-2bx+b+6=0
· Имеет отрицательные корни?
· Имеет корни разных знаков?
· Имеет положительные корни?
· Не имеет корней?
· Имеет корень, равный 0?
6) Найти все значения параметра a, при которых для уравнения x2-ax+4=0 выполняются следующие условия:
· Число 4 разделяет корни уравнения;
· Оба корня уравнения больше 4;
· Оба корня уравнения лежат в промежутке (1;4);
· Разность корней равна 4;
· Отношение корней равно 4.
7) При каких значениях параметра a неравенство x2+2ax+1<0 не имеет решения?
8) При каких значениях параметра a
· множеством решений неравенства x2+2ax+1≤ 0 является отрезок?
· множество решений неравенства состоит из одной точки?
9) При каких значениях параметра a неравенство ax2-4ax-3≤0 выполняется при всех значениях x?
10) При каких значениях параметра a неравенство ax2+(2a+3)x+a-1≥0 не имеет решения?
Задачи с параметром
11) При каких  число 1 является решением неравенства
число 1 является решением неравенства
 ?
?
12) Найдите значение параметра а, при котором наименьшее решение неравенства
 равно 2.
равно 2.
13) Найдите значение параметра а, при котором наибольшее решение неравенства
 равно 6.
равно 6.
14) Найдите значение параметра а, при котором наименьшее решение неравенства
 равно 10.
равно 10.
15) Найдите значение параметра р, при котором уравнение
 имеет единственный корень.
имеет единственный корень.
16) Найдите значение параметра р, при котором уравнение
 имеет единственный корень.
имеет единственный корень.
17) При каких значениях параметра а уравнение
 имеет ровно один корень?
имеет ровно один корень?
18) При каких значениях параметра а уравнение
 имеет единственный корень?
имеет единственный корень?
19) При каких в уравнение 
имеет ровно 2 различных корня?
20) Найдите все значения параметра а, при котором система

имеет решение.
| Задачи с параметром | Ответы |
| 1) При каких значениях параметра a уравнение (a2-4)x=a2+a-6 · Имеет бесконечно много решений? · Не имеет решений? · Имеет единственное решение? | |
| 2) При каких значениях параметра a неравенство xa2<a+x · Не имеет решений? · Выполняется для любых x? | |
| 3) При каких значениях параметра a система a + y - 0,5a2x = 0 8x – y + 4 = 0 · Имеет бесконечно много решений? · Не имеет решений? · Имеет единственное решение? | |
| 4) При каких значениях параметра b уравнение (2b-5)x2-2(b-1)x+3=0 · Имеет единственное решение? · Имеет два различных корня? | |
| 5) При каких значениях параметра b уравнение x2-2bx+b+6=0 · Имеет отрицательные корни? · Имеет корни разных знаков? · Имеет положительные корни? · Не имеет корней? · Имеет корень, равный 0? | |
| 6) Найти все значения параметра a, при которых для уравнения x2-ax+4=0 выполняются следующие условия: · Число 4 разделяет корни уравнения; · Оба корня уравнения больше 4; · Оба корня лежат в промежутке (1;4); · Разность корней равна 4; · Отношение корней равно 4. | |
| 7) При каких значениях параметра a неравенство x2+2ax+1<0 не имеет решения? | |
| 8) При каких значениях параметра a · множеством решений неравенства x2+2ax+1≤ 0 является отрезок? · множество решений неравенства состоит из одной точки? | |
| 9) При каких значениях параметра a неравенство ax2-4ax-3≤0 выполняется при всех значениях x? | |
| 10) При каких значениях параметра a неравенство ax2+(2a+3)x+a-1≥0 не имеет решения? |
| Задачи с параметром | Ответы |
11) При каких  число 1 является решением неравенства число 1 является решением неравенства  ? ?
| |
12) Найдите значение параметра а, при котором наименьшее решение неравенства  равно 2. равно 2.
| |
13) Найдите значение параметра а, при котором наибольшее решение неравенства  равно 6. равно 6.
| |
14) Найдите значение параметра а, при котором наименьшее решение неравенства  равно 10. равно 10.
| |
15) Найдите значение параметра р, при котором уравнение
 имеет единственный корень. имеет единственный корень.
| |
16) Найдите значение параметра р, при котором уравнение
 имеет единственный корень. имеет единственный корень.
| |
17) При каких значениях параметра а уравнение
 имеет ровно один корень? имеет ровно один корень?
| |
18) При каких значениях параметра а уравнение
 имеет единственный корень? имеет единственный корень?
| |
19) При каких в уравнение
 имеет ровно 2 различных корня?
имеет ровно 2 различных корня?
| |
20) Найдите все значения параметра а, при котором система
 имеет решение.
имеет решение.
|
| Задачи | Ответы |
1. При каких значениях a число 2 является корнем уравнения
 ?
2. Найти все значения параметра a, при которых уравнение ?
2. Найти все значения параметра a, при которых уравнение  не имеет решения.
3. Найти все значения параметра a, при которых уравнение не имеет решения.
3. Найти все значения параметра a, при которых уравнение 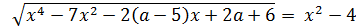 имеет хотя бы один корень.
4. Найти все значения параметра b, при которых уравнение
имеет хотя бы один корень.
4. Найти все значения параметра b, при которых уравнение
 = 2
имеет ровно два различных корня.
5. = 2
имеет ровно два различных корня.
5.
| 1. а = 1
2. а  - 4
3. а - 4
3. а   4. b
4. b  - 4 - 4
|
1) При каких значениях a число 2 является корнем уравнения
 ?
?
2) Найти все значения параметра a, при которых уравнение  не имеет решения.
не имеет решения.
3) Найти все значения параметра a, при которых уравнение 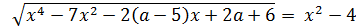
имеет хотя бы один корень.
4) Найти все значения параметра b, при которых уравнение
 =2
=2
имеет ровно два различных корня.
5)
Дата добавления: 2015-09-03; просмотров: 416 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Встановлення електрощита своїми руками | | | Д.м.н., профессор В.А. Романов |