Derivative for integers and rational numbers

Firstly, let us verify in one quite familiar property

“Theorem 9 A derivative is uniquely defined over the integers by the rule ” (Bains, Barbeau, Ufnarovski)

(-x)’=-x’

Secondly, we can expand operation for rational numbers. Using theorem 1 we can define it similar to standard property of the :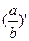

“Theorem 10 For any two rational numbers a, b we have ” (Bains, Barbeau, Ufnarovski)

A derivative can be well defined for rational numbers using this formula and this is the only way to define a derivative over rational numbers that preserves the Leibnitz rule. ” (Bains, Barbeau, Ufnarovski)

That rule is correct for both positive and negative rational numbers. Next thing which can be done is we can define the function for some irrational numbers. Unfortunately, that is hard due to rejection of the linearity. Another explanation is the following: it is quite easy to calculate the derivative of irrational numbers, containing only one operation of calculation of root (for example, sqrt(2) = 1/2). However it is quite unclear how the derivative of 1 + sqrt(2) should be calculated.

This undeveloped theory can be helpful to transfer our notion to complex numbers, since every complex number can be represented as a sum of real part and imaginary part. Here, the definition of Gauss prime numbers can help.

It is interesting to broaden the theory to transcendental numbers. It is evident that the derivative of a function exp(x) equals exp(x), that is to say, itself. But what about the number e and its multiplicative derivative? What about the number pi?

Line of activity.

All works and conclusions made by Ufnarovski, Barbeau and Bains are strictly theoretical. In my paperwork I shall focus on numerical experiments for sufficiently large natural numbers and their approximation, which was never done before. This could help to describe distribution of solutions of various equations. Here is the list of all hypothesizes which will be checked:

- Linear pairs, their density.

- Fixed points conjectures (of equation n’ = n), existence of any exterior roots.

- The numerical solution of the equation n’ = a (partly done in my previous work)

- The numerical solution of the equation n’ = 2b (connected with Goldbach’s conjecture)

- Numerical solution of the equation n’’ = 1 (connected with Prime Twins Conjecture)

- Development and expansion of multiplicative differentiation theory to the set of irrational and transcendental numbers.

Дата добавления: 2015-09-02