Note: practically all theorems and conjectures belong to Ufnarovski and Barbeau

Let n be a natural number (although we shall extend operation to greater sets of numbers). What we want to do is we want to define the operation of calculating the derivative such that (n; n’) = 1 if and only if n is square-free. As everybody knows, derivative has some nice properties such as 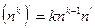(Leibnitz rule) and linearity. These properties are desired to be preserved. Because 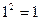we should have 1’=0 and as far as n’ = (1+1+….+1)’= 1’ + 1’ +… = 0 (according to linearity) we will have n’=0 for every natural number which doesn’t make any sense. For that reason, we should reject linearity and use the Leibnitz rule only. Next step is to connect primes with our operation, since all natural numbers depend on primes. Taking into account all aspects described above, we can define the derivative of a natural number as a function with two simple properties:

I (ab)’ = a’b + b’a

II p’ = 1 for any prime p;

For example, here is the calculation of the derivative of a natural number 10

10’ = (2*5)’ = 2’*5 + 5’*2 = 1*5 + 1*2 = 7

Below you can see the table in which the operation was used to calculate the derivative of first 18 natural numbers (meaning from 1 to 18)

n

n’

n’’

n’’’

From the first sight this operation looks strange. But before continuing with its usage it is sufficient to prove that our operation is well-defined.

“Theorem 1 The derivative n’ can be well-defined as follows: if n = 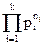is a factorization in prime powers, then

n’ =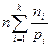

It is the only way to define n’ that satisfies desired properties. ” (Bains, Barbeau, Ufnarovski)

Here is an example of calculating the derivative of natural number 60:

(60)’ = (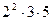)’ = = 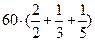60 + 20+12 = 92

This formula will be used further in every approximating program of the work.

It would be nice to extend the definition for 0, so we shall have 0’ = 0, since it doesn’t contradict the Leibnitz rule and clear on the intuitive level.

We have to remember, that the linearity doesn’t hold, since for dominating majority of natural numbers a, b we have (a + b)’ 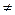a’+b’. In addition to that, (ab)’’ 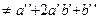since this property allocates with linearity. In my work I shall make an attempt of describing all pairs (a; b) for which linearity holds (meaning that they satisfy the equation (a + b)’ = a’+b’). We can call them “Linear pairs”. It is easy to find the solution (4; 8) (see the table above). What is interesting, we can obtain that solution from the pair (1; 2) by using the following result (described by Ufnarovsky and Barbeau).

“Theorem 2 If (a + b)’=a’+b’, then for any natural k we have (ka+kb)’ = (ka)’+(kb)’, the same holds for the inequalities. ” (Bains, Barbeau, Ufnarovski)

In addition to that,

“Theorem 3 For any natural k > 1; ” (Bains, Barbeau, Ufnarovski)

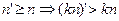
This two theorems will be used to program calculus solution and approximate the function which can help us to find all “Linear pairs”

Now, as we finished describing properties of our map, we shall proceed with differential equations on the set of natural numbers.

The equation n’ = n

This equation is interesting from the following scientific point of view: it factually returns all fixed points of our function:

“Theorem 4 The equation n’ = n holds if and only 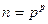; where p is any prime number. In particular, it has infinitely many solutions in natural numbers.

Conjecture 1 There exist infinitely many composite numbers n such that 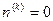for sufficiently large natural k: ” (Bains, Barbeau, Ufnarovski)

This Conjecture has a connection with the Twin Prime Conjecture in the following way: if this conjecture is false, then the Twin Prime conjecture is false to. According to different numerical experiments, the derivative 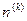either becomes zero or tends to infinity. But nobody knows whether this statement is true or false yet.

This unsolved conjecture perfectly fits the situation described in the abstract – sometimes it is quite hard to solve the problem in its native formulation, however it can be much easier to do that in the reformulation,

“Conjecture 2 Exactly one of the following could happen: either 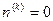for sufficiently large k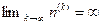; or , or 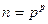for some prime p.

Conjecture 3 The differential equation 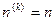has only trivial solutions 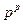for primes p. ” (Bains, Barbeau, Ufnarovski)

That conjecture obviously rises a question: are there any other fixed points different from 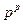? If there are any, do they own any interesting properties which can simplify investigation of our function?

Now let’s proceed with the most general case.

The equation n’=a

Firstly, let us solve two easy equations:

“Theorem 5 The differential equation 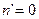has only one positive integer solution n = 1. ” (Bains, Barbeau, Ufnarovski)

It is very simple, and follows immediately from the definition of our operation.

“Theorem 6 The differential equation 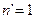in natural numbers has only primes as solutions. ” (Bains, Barbeau, Ufnarovski)

That theorem is also quite simple and reformulates the definition of primes.

Now I would like to describe fundamental inequality which will be used in almost every approximation applied to that paperwork in the nearest future.

“Theorem 7 For any positive integer n

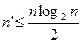
If n is not a prime, then

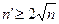
More generally, if n is a product of k factors larger than 1, then

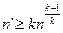. ” (Bains, Barbeau, Ufnarovski)

We need this for the following reasons: since there are no mathematic methods of solving such equations, the only way to solve them is a straightforward brootforce. In order to check whether the natural number is a solution or not, we should have the upper bound (the greatest natural number) till which we need to check. These inequalities provide us with such a bound.

“Conjecture 4 The differential equation n’ = 2b has a natural solution for any natural number b > 1. ” (Bains, Barbeau, Ufnarovski)

The proof of this conjecture is very demanded, since it includes famous:

Goldbach Conjecture Every even number larger than 3 is a sum of two primes.

That problem is also known as binary Goldbach Conjecture or Eiler problem. It was formulated in 1742 in correspondence between Christian Goldbach and Leonard Eiler, It remains unproved up to present days. In my work one of anticipated results is to approximate calculus solution of differential equation described in Conjecture 5.

The reformulation is quite simple: it is evident, that if 2b = p + q; then n = pq is a desired solution. By using the fundamental inequality described above, it is easy to check that the equation n’ = 2 has no solutions in natural numbers. The same holds for an equation n’ = 3. But for another numbers we can formulate a theorem, which helps us to find some solutions which are close to primes:

“Theorem 8 Let p be a prime and a = p + 2. Then 2p is a solution for the equation n’ = a. ” (Bains, Barbeau, Ufnarovski)

Note that for all a which remain prime (meaning if a = p+2 is prime when p is prime) we have a connection with Twin Prime Conjecture. By using this we can obtain some primes, as a value of our function.

Next question is: for which natural numbers the equation has no solutions as primes? Here is a list of all a 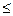1000 for which the equation n’ = a has no solutions (obtained by Unfnarovsky and later myself using Matlab and fundamental inequality):

2; 3; 11; 17; 23; 29; 35; 37; 47; 53; 57; 65; 67; 79; 83; 89; 93; 97; 107; 117; 125; 127;

137; 145; 149; 157; 163; 173; 177; 179; 189; 197; 205; 207; 209; 217; 219; 223; 233;

237; 245; 257; 261; 277; 289; 303; 305; 307; 317; 323; 325; 337; 345; 353; 367; 373;

377; 379; 387; 389; 393; 397; 409; 413; 415; 427; 429; 443; 449; 453; 457; 473; 477;

485; 497; 499; 509; 513; 515; 517; 529; 531; 533; 537; 547; 553; 561; 569; 577; 593;

597; 605; 613; 625; 629; 639; 657; 659; 665; 673; 677; 681; 683; 697; 699; 709; 713;

715; 733; 747; 749; 757; 765; 769; 777; 781; 783; 785; 787; 793; 797; 805; 809; 817;

819; 827; 833; 835; 845; 847; 849; 853; 857; 869; 873; 877; 881; 891; 895; 897; 907;

917; 925; 933; 937; 947; 953; 963; 965; 967; 981; 989; 997:

An interesting thing is that not all of them are primes (less than half of them actually) In 2011 my course work was dedicated to research of the function i(a) which returns the value of the amount of solutions of the equation n’ = a. In that work I had taken an attempt to approximate the function i(a) using logarithm; in addition to that I have tried to investigate the density of all natural a for which an equation n’=a has no solutions. Results of these researches and dedicated graphs can be found in appendix.

The question connected with this function can be formulated as another conjecture:

Conjecture 7 For any nonnegative m there exists infinitely many a such that i(a) = m.

Now let’s proceed to the equation which has a second derivative with the variable.

The equation n’’ = 1

That equation gives a birth to a question which is directly connected to Prime Twins Conjecture:

“Conjecture 5 The differential equation n’’ = 1 has infinitely many solutions in natural numbers. ” (Bains, Barbeau, Ufnarovski)

It is evident that n = 2*p is a solution if p + 2 and p are prime numbers. Indeed,

(2p)’ = p +2 and (p+2)’ = 1

We could also formulate our own conjecture: are there any natural numbers for which n’’=1 and they don’t have the form of 2*p. If there are any, do the hold any interesting properties? That question will be checked with the usage of computer.

Now we end with natural numbers. Next step is to expand the operation to integers.

Дата добавления: 2015-09-02