классу к 28 октября

1. В сред­нем из 1000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 5 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

Ре­ше­ние.

в сред­нем из 1000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 1000 − 5 = 995 не под­те­ка­ют. Зна­чит, ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет, равна

Ответ: 0,995.

Ответ: 0,995

2. Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 35 этих сте­кол, вто­рая – 65 . Пер­вая фаб­ри­ка вы­пус­ка­ет 3 бра­ко­ван­ных сте­кол, а вто­рая – 5 . Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.

Ре­ше­ние.

Ве­ро­ят­ность того, что стек­ло куп­ле­но на пер­вой фаб­ри­ке и оно бра­ко­ван­ное: 0,35 · 0,03 = 0,0105.

Ве­ро­ят­ность того, что стек­ло куп­ле­но на вто­рой фаб­ри­ке и оно бра­ко­ван­ное: 0,65 · 0,05 = 0,0325.

По­это­му по фор­му­ле пол­ной ве­ро­ят­но­сти ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным равна 0,0105 + 0,0325 = 0,043.

Ответ: 0,043.

Ответ: 0,043

3. В фирме такси в дан­ный мо­мент сво­бод­но 35 машин: 11 крас­ных, 17 фи­о­ле­то­вых и 7 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет зе­ле­ное такси.

Ре­ше­ние.

Ве­ро­ят­ность того, что к за­каз­чи­це при­е­дет зе­ле­ное такси равна

.

Ответ: 0,2.

Ответ: 0,2

4.

Сред­няя линия и вы­со­та тра­пе­ции равны со­от­вет­ствен­но 28 и 4. Най­ди­те пло­щадь тра­пе­ции.

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. Сред­няя линия тра­пе­ции равна по­лу­сум­ме ос­но­ва­ний. По­это­му

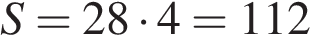см².

Ответ: 112.

Ответ: 112

5.

Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на ри­сун­ке.

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. По­это­му

см².

Ответ: 16.

Ответ: 16

6. Ве­ро­ят­ность того, что ба­та­рей­ка бра­ко­ван­ная, равна 0,06. По­ку­па­тель в ма­га­зи­не вы­би­ра­ет слу­чай­ную упа­ков­ку, в ко­то­рой две таких ба­та­рей­ки. Най­ди­те ве­ро­ят­ность того, что обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми.

Ре­ше­ние.

Ве­ро­ят­ность того, что ба­та­рей­ка ис­прав­на, равна 0,94. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий (обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми) равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,94·0,94 = 0,8836.

Ответ: 0,8836.

Ответ: 0,8836

7. Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,4. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 2 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.

Ре­ше­ние.

Джон про­мах­нет­ся, если схва­тит при­стре­лян­ный ре­воль­вер и про­мах­нет­ся из него, или если схва­тит не­при­стре­лян­ный ре­воль­вер и про­мах­нет­ся из него. По фор­му­ле услов­ной ве­ро­ят­но­сти, ве­ро­ят­но­сти этих со­бы­тий равны со­от­вет­ствен­но 0,2·(1 − 0,9) = 0,02 и 0,8·(1 − 0,4) = 0,48. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,02 + 0,48 = 0,5.

Ответ: 0,5.

Ответ: 0,5

8. Иг­раль­ный кубик бро­са­ют два­жды. Сколь­ко эле­мен­тар­ных ис­хо­дов опыта бла­го­при­ят­ству­ют со­бы­тию «А = сумма очков равна 5»?

Ре­ше­ние.

Сумма очков может быть равна 5 в че­ты­рех слу­ча­ях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».

Ответ: 4.

Ответ: 4

9. На се­ми­нар при­е­ха­ли 3 уче­ных из Нор­ве­гии, 3 из Рос­сии и 4 из Ис­па­нии. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Най­ди­те ве­ро­ят­ность того, что вось­мым ока­жет­ся до­клад уче­но­го из Рос­сии.

Ре­ше­ние.

Всего в се­ми­на­ре при­ни­ма­ет уча­стие 3 + 3 + 4 = 10 уче­ных, зна­чит, ве­ро­ят­ность того, что уче­ный, ко­то­рый вы­сту­па­ет вось­мым, ока­жет­ся из Рос­сии, равна 3:10 = 0,3.

Ответ: 0,3.

Ответ: 0,3

10. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

Ре­ше­ние.

Рас­смот­рим со­бы­тия

А = кофе за­кон­чит­ся в пер­вом ав­то­ма­те,

В = кофе за­кон­чит­ся во вто­ром ав­то­ма­те.

Тогда

A·B = кофе за­кон­чит­ся в обоих ав­то­ма­тах,

A + B = кофе за­кон­чит­ся хотя бы в одном ав­то­ма­те.

По усло­вию P(A) = P(B) = 0,3; P(A·B) = 0,12.

Со­бы­тия A и B сов­мест­ные, ве­ро­ят­ность суммы двух сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий, умень­шен­ной на ве­ро­ят­ность их про­из­ве­де­ния:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

Сле­до­ва­тель­но, ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что кофе оста­нет­ся в обоих ав­то­ма­тах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

При­ве­дем дру­гое ре­ше­ние.

Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом ав­то­ма­те равна 1 − 0,3 = 0,7. Ве­ро­ят­ность того, что кофе оста­нет­ся во вто­ром ав­то­ма­те равна 1 − 0,3 = 0,7. Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом или вто­ром ав­то­ма­те равна 1 − 0,12 = 0,88. По­сколь­ку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, от­ку­да ис­ко­мая ве­ро­я­тость х = 0,52.

При­ме­ча­ние.

За­ме­тим, что со­бы­тия А и В не яв­ля­ют­ся не­за­ви­си­мы­ми. Дей­стви­тель­но, ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий была бы равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: P(A·B) = 0,3·0,3 = 0,09, од­на­ко по усло­вию эта ве­ро­ят­ность равна 0,12.

Ответ: 0,52

11. На эк­за­ме­не по гео­мет­рии школь­ни­ку достаётся один во­прос из спис­ка эк­за­ме­на­ци­он­ных во­про­сов. Ве­ро­ят­ность того, что это во­прос на тему «Впи­сан­ная окруж­ность», равна 0,2. Ве­ро­ят­ность того, что это во­прос на тему «Па­рал­ле­ло­грамм», равна 0,15. Во­про­сов, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам, нет. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся во­прос по одной из этих двух тем.

Ре­ше­ние.

Ве­ро­ят­ность суммы двух не­сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

Ответ: 0,35

12. Фаб­ри­ка вы­пус­ка­ет сумки. В сред­нем на 100 ка­че­ствен­ных сумок при­хо­дит­ся во­семь сумок со скры­ты­ми де­фек­та­ми. Най­ди­те ве­ро­ят­ность того, что куп­лен­ная сумка ока­жет­ся ка­че­ствен­ной. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

По усло­вию на каж­дые 100 + 8 = 108 сумок при­хо­дит­ся 100 ка­че­ствен­ных сумок. Зна­чит, ве­ро­ят­ность того, что куп­лен­ная сумка ока­жет­ся ка­че­ствен­ной, равна

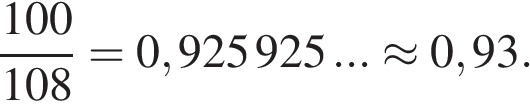
Ответ: 0,93.

Ответ: 0,93

13. В сбор­ни­ке би­ле­тов по био­ло­гии всего 55 би­ле­тов, в 11 из них встре­ча­ет­ся во­прос по бо­та­ни­ке. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку до­ста­нет­ся во­прос по бо­та­ни­ке.

Ре­ше­ние.

Ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку до­ста­нет­ся во­прос по бо­та­ни­ке, равна

Ответ: 0,2.

Ответ: 0,2

14. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 10 очков. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

Ко­ли­че­ство ис­хо­дов, при ко­то­рых в ре­зуль­та­те брос­ка иг­раль­ных ко­стей вы­па­дет 10 очков, равно 3: 4+6, 5+5, 6+4. Каж­дый из ку­би­ков может вы­пасть ше­стью ва­ри­ан­та­ми, по­это­му общее число ис­хо­дов равно 6·6 = 36. Сле­до­ва­тель­но, ве­ро­ят­ность того, что в сумме вы­па­дет 10 очков, равна

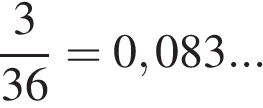
Ответ: 0,08.

Ответ: 0,08

15.

Най­ди­те пло­щадь ромба, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей. По­это­му

см².

Ответ: 6.

Ответ: 6

16. На эк­за­ме­не 40 во­про­сов, Игорь не вы­учил 2 из них. Най­ди­те ве­ро­ят­ность того, что ему по­па­дет­ся вы­учен­ный во­прос.

Ре­ше­ние.

Игорь вы­учил 40 – 2 = 38 во­про­сов. Тогда ве­ро­ят­ность того, что на эк­за­ме­не ему по­па­дет­ся вы­учен­ный во­прос равна

.

Ответ: 0,95.

Ответ: 0,95

17. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют три иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 6 очков. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

Ко­ли­че­ство ис­хо­дов, при ко­то­рых в ре­зуль­та­те брос­ка иг­раль­ных ко­стей вы­па­дет 6 очков, равно 10: 1 + 1 + 4, 1 + 4 + 1, 4 + 1 + 1, 1 + 2 + 3, 1 + 3 + 2, 3 + 1 + 2, 3 + 2 + 1, 2 + 1 + 3, 2 + 3 + 1, 2 + 2 + 2. Каж­дый из ку­би­ков может вы­пасть ше­стью ва­ри­ан­та­ми, по­это­му общее число ис­хо­дов равно 6 · 6 · 6 = 216. Сле­до­ва­тель­но, ве­ро­ят­ность того, что в сумме вы­па­дет 6 очков, равна

Ответ: 0,05.

Ответ: 0,05

18.

На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. По­это­му

см².

Ответ: 14.

Ответ: 14

19. В сбор­ни­ке би­ле­тов по ма­те­ма­ти­ке всего 25 би­ле­тов, в 10 из них встре­ча­ет­ся во­прос по не­ра­вен­ствам. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку не до­ста­нет­ся во­про­са по не­ра­вен­ствам.

Ре­ше­ние.

Из 25 би­ле­тов 15 не со­дер­жат во­про­са по не­ра­вен­ствам, по­это­му ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку не до­ста­нет­ся во­про­са по не­ра­вен­ствам, равна

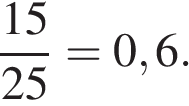
Ответ: 0,6.

Ответ: 0,6

20. Би­ат­ло­нист пять раз стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,8. Най­ди­те ве­ро­ят­ность того, что би­ат­ло­нист пер­вые три раза попал в ми­ше­ни, а по­след­ние два про­мах­нул­ся. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

По­сколь­ку би­ат­ло­нист по­па­да­ет в ми­ше­ни с ве­ро­ят­но­стью 0,8, он про­ма­хи­ва­ет­ся с ве­ро­ят­но­стью 1 − 0,8 = 0,2. Cобы­тия по­пасть или про­мах­нуть­ся при каж­дом вы­стре­ле не­за­ви­си­мы, ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию их ве­ро­ят­но­стей. Тем самым, ве­ро­ят­ность со­бы­тия «попал, попал, попал, про­мах­нул­ся, про­мах­нул­ся» равна

Ответ: 0,02.

Ответ: 0,02

21. В со­рев­но­ва­ни­ях по тол­ка­нию ядра участ­ву­ют 6 спортс­ме­нов из Ве­ли­ко­бри­та­нии, 3 спортс­ме­на из Фран­ции, 6 спортс­ме­нов из Гер­ма­нии и 10 — из Ита­лии. По­ря­док, в ко­то­ром вы­сту­па­ют спортс­ме­ны, опре­де­ля­ет­ся жре­би­ем. Най­ди­те ве­ро­ят­ность того, что спортс­мен, ко­то­рый вы­сту­па­ет по­след­ним, ока­жет­ся из Фран­ции.

Ре­ше­ние.

Всего в со­рев­но­ва­ни­ях при­ни­ма­ет уча­стие 6 + 3 + 6 + 10 = 25 спортс­ме­нов. Зна­чит, ве­ро­ят­ность того, что спортс­мен, ко­то­рый вы­сту­па­ет по­след­ним, ока­жет­ся из Фран­ции, равна

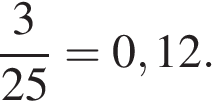
Ответ: 0,12.

Ответ: 0,12

22. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, если две его сто­ро­ны равны 47 и 2, а угол между ними равен 30°.

Ре­ше­ние.

Пло­щадь па­рал­ле­ло­грам­ма равна про­из­ве­де­нию его сто­рон на синус угла между ними. По­это­му

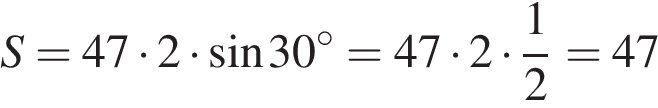см².

Ответ: 47.

Ответ: 47

23. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 10 чер­ных, 2 жел­тых и 8 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет зе­ле­ное такси.

Ре­ше­ние.

Ве­ро­ят­ность того, что к за­каз­чи­це при­е­дет зе­ле­ное такси равна

.

Ответ: 0,4.

Ответ: 0,4

24. На­уч­ная кон­фе­рен­ция про­во­дит­ся в 5 дней. Всего за­пла­ни­ро­ва­но 75 до­кла­дов — пер­вые три дня по 17 до­кла­дов, осталь­ные рас­пре­де­ле­ны по­ров­ну между чет­вер­тым и пятым днями. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции?

Ре­ше­ние.

За пер­вые три дня будет про­чи­тан 51 до­клад, на по­след­ние два дня пла­ни­ру­ет­ся 24 до­кла­да. По­это­му на по­след­ний день за­пла­ни­ро­ва­но 12 до­кла­дов. Зна­чит, ве­ро­ят­ность того, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции, равна

Ответ: 0,16.

Ответ: 0,16

25. Най­ди­те (в см²) пло­щадь фи­гу­ры, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). В от­ве­те за­пи­ши­те .

Ре­ше­ние.

Пло­щадь фи­гу­ры равна одной чет­вер­той пло­ща­ди круга, ра­ди­ус ко­то­ро­го равен см. По­это­му

см².

Ответ: 2,25.

Ответ: 2,25

26. Мак­сим с папой решил по­ка­тать­ся на ко­ле­се обо­зре­ния. Всего на ко­ле­се 30 ка­би­нок, из них 11 – синие, 7 – зе­ле­ные, осталь­ные – оран­же­вые. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для по­сад­ки. Най­ди­те ве­ро­ят­ность того, что Мак­сим про­ка­тит­ся в оран­же­вой ка­бин­ке.

Ре­ше­ние.

на ко­ле­се обо­зре­ния 30–11–7=12 оран­же­вых ка­би­нок. Тогда ве­ро­ят­ность того, что Мак­сим про­ка­тит­ся в оран­же­вой ка­бин­ке равна

.

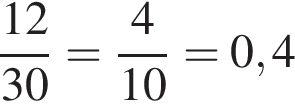Ответ: 0,4.

Ответ: 0,4

27. Ве­ро­ят­ность того, что новый DVD-про­иг­ры­ва­тель в те­че­ние года по­сту­пит в га­ран­тий­ный ре­монт, равна 0,045. В не­ко­то­ром го­ро­де из 1000 про­дан­ных DVD-про­иг­ры­ва­те­лей в те­че­ние года в га­ран­тий­ную ма­стер­скую по­сту­пи­ла 51 штука. На сколь­ко от­ли­ча­ет­ся ча­сто­та со­бы­тия «га­ран­тий­ный ре­монт» от его ве­ро­ят­но­сти в этом го­ро­де?

Ре­ше­ние.

Ча­сто­та (от­но­си­тель­ная ча­сто­та) со­бы­тия «га­ран­тий­ный ре­монт» равна 51: 1000 = 0,051. Она от­ли­ча­ет­ся от пред­ска­зан­ной ве­ро­ят­но­сти на 0,006.

Ответ: 0,006.

Ответ: 0,006

28. На борту самолёта 12 мест рядом с за­пас­ны­ми вы­хо­да­ми и 18 мест за пе­ре­го­род­ка­ми, раз­де­ля­ю­щи­ми са­ло­ны. Осталь­ные места не­удоб­ны для пас­са­жи­ра вы­со­ко­го роста. Пас­са­жир В. вы­со­ко­го роста. Най­ди­те ве­ро­ят­ность того, что на ре­ги­стра­ции при слу­чай­ном вы­бо­ре места пас­са­жи­ру В. до­ста­нет­ся удоб­ное место, если всего в самолёте 300 мест.

Ре­ше­ние.

В са­мо­ле­те 12 + 18 = 30 мест удоб­ны пас­са­жи­ру В., а всего в са­мо­ле­те 300 мест. По­это­му ве­ро­ят­ность того, что пас­са­жи­ру В. до­ста­нет­ся удоб­ное место равна 30: 300 = 0,1.

Ответ: 0,1.

Ответ: 0,1

29. В кар­ма­не у Миши было че­ты­ре кон­фе­ты — «Гри­льяж», «Бе­лоч­ка», «Ко­ров­ка» и «Ла­сточ­ка», а также ключи от квар­ти­ры. Вы­ни­мая ключи, Миша слу­чай­но вы­ро­нил из кар­ма­на одну кон­фе­ту. Най­ди­те ве­ро­ят­ность того, что по­те­ря­лась кон­фе­та «Гри­льяж».

Ре­ше­ние.

В кар­ма­не было 4 кон­фе­ты, а вы­па­ла одна кон­фе­та. По­это­му ве­ро­ят­ность этого со­бы­тия равна одной чет­вер­той.

Ответ: 0,25.

Ответ: 0,25

30. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе.

Дата добавления: 2015-09-02