
Читайте также:
|
1°. Определение эллипса, каноническое уравнение эллипса, исследование формы эллипса.
Определение 1. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек  и
и 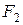 этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.
этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая, чем расстояние между фокусами.
Составим уравнение эллипса. Выберем на плоскости декартову прямоугольную систему координат так, чтобы ось  проходила через фокусы
проходила через фокусы  и
и 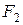 , и имела одинаковое направление с вектором
, и имела одинаковое направление с вектором 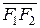 , а начало координат
, а начало координат  было в середине отрезка
было в середине отрезка  . Пусть
. Пусть  . Тогда
. Тогда  – координаты фокуса
– координаты фокуса  а
а  – координаты фокуса
– координаты фокуса 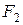 (рис.1).
(рис.1).

Рис. 1
Пусть  – произвольная точка эллипса. Отрезки
– произвольная точка эллипса. Отрезки  и
и  называются фокальными радиусами точки
называются фокальными радиусами точки  . Положим
. Положим  ,
, 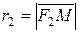 Тогда
Тогда
 ,
,  . (1)
. (1)
Согласно определению эллипса, точка  принадлежит эллипсу тогда и только тогда, когда для некоторого числа
принадлежит эллипсу тогда и только тогда, когда для некоторого числа  , большего
, большего  , выполняется равенство
, выполняется равенство
 . (2)
. (2)
Уравнение (2) является уравнением эллипса в выбранной декартовой прямоугольной системе координат.
Представим уравнение (2) в виде

и возведём обе части в квадрат. Получим
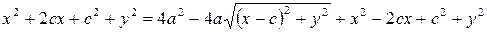 ,
,
откуда
 .
.
Вновь доведём обе части этого равенства в квадрат:
 ,
,
откуда
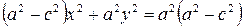 , (3)
, (3)
причём  .
.
Положим  , тогда из (5) следует
, тогда из (5) следует
 . (4)
. (4)
Таким образом, координаты любой точки эллипса удовлетворяют уравнению (4). Покажем теперь, что верно и обратное утверждение: любая точка  , координаты которой удовлетворяют уравнению
, координаты которой удовлетворяют уравнению  , есть точка эллипса. Для этого убедимся, что
, есть точка эллипса. Для этого убедимся, что 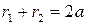 . Подставив значение
. Подставив значение  из (4) в правую часть выражений (1), получим
из (4) в правую часть выражений (1), получим
 ,
,
откуда
 ,
,  .
.
Так как из уравнения (4) следует  , т.е.
, т.е.  ,
,  , то
, то  , а это значит, что
, а это значит, что  . Следовательно,
. Следовательно,
 ,
,  . (5)
. (5)
Отсюда получаем  , а это значит, что точка
, а это значит, что точка  принадлежит эллипсу.
принадлежит эллипсу.
Уравнение (4) называется каноническим уравнением эллипса. Числа  и
и  называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.
Исследуем форму эллипса. Из канонического уравнения эллипса (4) следует, что  ,
,  . Это означает, что эллипс расположен в прямоугольнике, образованном прямыми
. Это означает, что эллипс расположен в прямоугольнике, образованном прямыми  ,
,  , и, следовательно, является ограниченной кривой.
, и, следовательно, является ограниченной кривой.
Так как каноническое уравнение эллипса содержит только квадраты текущих координат, то из принадлежности точки  эллипсу следует, что и точки
эллипсу следует, что и точки  ,
,  ,
,  также лежат на эллипсе. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии.
также лежат на эллипсе. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии. Таким образом, оси координат являются осями симметрии эллипса, а начало координат – центром симметрии.

Рис. 2
Если в уравнении (4) положим  , то получим
, то получим  или
или 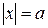 . Значит,
. Значит,  ,
,  – точки пересечения эллипса с осью
– точки пересечения эллипса с осью  .
.
Полагая  , получаем
, получаем  , т.е. точками пересечения эллипса с осью
, т.е. точками пересечения эллипса с осью  являются
являются  ,
,  . Точки
. Точки  ,
,  называются вершинами эллипса.
называются вершинами эллипса.
В силу симметрии достаточно исследовать форму эллипса только в первой четверти. Для первой четверти из уравнения (6) получим
 .
.
Функция  определена и непрерывна при
определена и непрерывна при  , поэтому график функции асимптот не имеет. Вычислим производные
, поэтому график функции асимптот не имеет. Вычислим производные

и найдём, что при  производные
производные 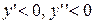 . Следовательно, данная функция монотонно убывает и выпукла вверх. График функции
. Следовательно, данная функция монотонно убывает и выпукла вверх. График функции  в первой четверти изображён на рис. 2. Эллипс строим с учётом симметрии (см. рис. 1).
в первой четверти изображён на рис. 2. Эллипс строим с учётом симметрии (см. рис. 1).
Определение 2. Число
 (6)
(6)
называется эксцентриситетом эллипса.
Так как  , то
, то 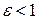 . Перепишем формулу (6) для эксцентриситета в виде
. Перепишем формулу (6) для эксцентриситета в виде
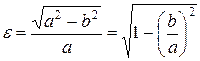 .
.
Отсюда видно, что  характеризует форму эллипса: если
характеризует форму эллипса: если  , то
, то 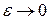 , а эллипс становится похожим на окружность. При увеличении
, а эллипс становится похожим на окружность. При увеличении  эллипс становится более вытянутым.
эллипс становится более вытянутым.
Пусть  – произвольная точка эллипса. Её фокальные радиусы
– произвольная точка эллипса. Её фокальные радиусы  и
и 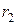 задаются формулами (5), которые в силу (6) имеют вид
задаются формулами (5), которые в силу (6) имеют вид
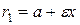 ,
,  . (7)
. (7)
Восстановим в одном из фокусов  эллипса перпендикуляр к оси
эллипса перпендикуляр к оси  до пересечения в точке
до пересечения в точке  с эллипсом. Фокальным параметром
с эллипсом. Фокальным параметром  эллипса называется длина отрезка
эллипса называется длина отрезка  .
.
Так как точка  имеет координаты
имеет координаты  , то
, то
 ,
,
откуда  , т.е.
, т.е. 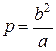 .
.
Выведем параметрическое уравнение эллипса. Перейдём в каноническом уравнении эллипса (4) к переменным
 .
.
Получим уравнение окружности  . Параметрическое уравнение этой окружности, как известно, имеет вид
. Параметрическое уравнение этой окружности, как известно, имеет вид  . Тогда
. Тогда
 .
.
Полученные уравнения являются параметрическими уравнениями эллипса.
2°. Определение гиперболы, каноническое уравнение гиперболы, исследование формы гиперболы.
Определение 3. Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек  и
и 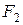 этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Пусть расстояние между фокусами равно  . Для вывода канонического уравнения гиперболы выберем ДПСК так же, как и для эллипса. Тогда фокус
. Для вывода канонического уравнения гиперболы выберем ДПСК так же, как и для эллипса. Тогда фокус  имеет координаты
имеет координаты  , а фокус
, а фокус 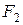 – координаты
– координаты  .
.
Для произвольной точки  плоскости определим её фокальные радиусы
плоскости определим её фокальные радиусы  и
и 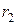 по формулам:
по формулам:  ,
, 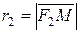 . По определению, точка
. По определению, точка  принадлежит гиперболе, если
принадлежит гиперболе, если  есть величина постоянная. Пусть
есть величина постоянная. Пусть  . Это равенство является необходимым и достаточным условием расположения точки
. Это равенство является необходимым и достаточным условием расположения точки  на данной гиперболе. Из этого равенства, используя выражения (1) для фокальных радиусов
на данной гиперболе. Из этого равенства, используя выражения (1) для фокальных радиусов  и
и 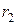 , получаем уравнение
, получаем уравнение
 , (8)
, (8)
являющиеся уравнением гиперболы в выбранной прямоугольной системе координат. Переписывая (8) в виде
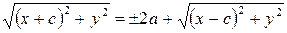
и возведя обе части равенства в квадрат, получим
 .
.
Отсюда упрощений имеем
 .
.
Возведя обе части снова в квадрат, получим
 ,
,
откуда
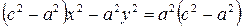 .
.
Так как для гиперболы  , то, положив
, то, положив  , получим
, получим
 . (9)
. (9)
Мы показали, что координаты любой точки гиперболы удовлетворяют уравнению (9). Покажем теперь, что справедливо и обратное утверждение: любая точка  с координатами
с координатами  , удовлетворяющими уравнению (9), есть точка гиперболы.
, удовлетворяющими уравнению (9), есть точка гиперболы.
Из (9) находим  . Тогда
. Тогда
 .
.
Аналогично получим
 .
.
Так как из равенства (13) следует, что  и, по определению,
и, по определению,  , то для
, то для  имеем
имеем
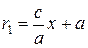 ,
,  , (10)
, (10)
поэтому  . Для
. Для 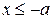 получим
получим
 ,
,  . (11)
. (11)
Следовательно, 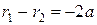 .
.
Таким образом, для рассматриваемой точки  имеем
имеем  , и поэтому она располагается на гиперболе. Уравнение (9) называется каноническим уравнением гиперболы.
, и поэтому она располагается на гиперболе. Уравнение (9) называется каноническим уравнением гиперболы.
Исследуем форму гиперболы.Так как в уравнение (9) входят только чётные степени координат, то, как и в случае эллипса, оси координат являются осями симметрии, а начало координат – центром симметрии. Ось симметрии гиперболы, на которой располагаются фокусы, называется фокальной осью, а точка пересечения осей симметрии – центром гиперболы.
Точки пересечения гиперболы с осями симметрии называются вершинами. Полагая  в уравнении (9), получаем
в уравнении (9), получаем  – точка пересечения гиперболы с осью
– точка пересечения гиперболы с осью  . Следовательно, точки
. Следовательно, точки  ,
,  – вершины гиперболы. Положив
– вершины гиперболы. Положив  , из (9) получим невозможное равенство
, из (9) получим невозможное равенство  , которое означает, что гипербола не пересекается с осью
, которое означает, что гипербола не пересекается с осью  .
.
Величина  и
и  называются полуосями гиперболы. Если
называются полуосями гиперболы. Если 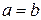 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Из уравнения (9) получаем
 ,
,
т.е.  . В силу симметрии достаточно исследовать форму гиперболы в первой четверти, а в остальных четвертях построить гиперболу по симметрии. Из уравнения (9) для первой четверти получаем
. В силу симметрии достаточно исследовать форму гиперболы в первой четверти, а в остальных четвертях построить гиперболу по симметрии. Из уравнения (9) для первой четверти получаем
 . (12)
. (12)
Функция  в первой четверти монотонно возрастает и является выпуклой вверх, так как
в первой четверти монотонно возрастает и является выпуклой вверх, так как
 ,
,
 .
.
Найдём наклонную асимптоту  для графика функции (12) в первой четверти:
для графика функции (12) в первой четверти:
 ,
,
 .
.
Следовательно, прямая  – наклонная асимптота для гиперболы. В силу симметрии асимптотами гиперболы (9) являются прямые
– наклонная асимптота для гиперболы. В силу симметрии асимптотами гиперболы (9) являются прямые  . Других асимптот нет.
. Других асимптот нет.
Построим гиперболу (9). Сначала построим так называемый основной прямоугольник гиперболы со сторонами  ,
,  . Очевидно, что асимптоты гиперболы являются прямыми, на которых расположены диагонали этого прямоугольника. Из приведённых выше рассуждений следует, что гипербола имеет вид, изображённый на рис. 3, и состоит из левой и правой ветвей.
. Очевидно, что асимптоты гиперболы являются прямыми, на которых расположены диагонали этого прямоугольника. Из приведённых выше рассуждений следует, что гипербола имеет вид, изображённый на рис. 3, и состоит из левой и правой ветвей.
Рассмотрим также уравнение
 . (13)
. (13)
Оно задаёт гиперболу, фокусы которой расположены на оси  , а основной прямоугольник и асимптота те же, что у гиперболы (9) (рис. 4). Гиперболы (9) и (13) называются сопряжёнными друг с другом.
, а основной прямоугольник и асимптота те же, что у гиперболы (9) (рис. 4). Гиперболы (9) и (13) называются сопряжёнными друг с другом.

Рис. 3

Рис. 4
Определение 4. Эксцентриситетом гиперболы называется число
 .
.
Для любой гиперболы 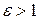 . Эксцентриситет характеризует форму гиперболы: чем меньше
. Эксцентриситет характеризует форму гиперболы: чем меньше  , тем больше вытягивается основной прямоугольник (так как
, тем больше вытягивается основной прямоугольник (так как  ), а вслед за ним и гипербола вдоль оси
), а вслед за ним и гипербола вдоль оси  .
.
Фокальным параметром  гиперболы называется длина отрезка перпендикуляра к оси
гиперболы называется длина отрезка перпендикуляра к оси  , восстановленного в одном из фокусов до пересечения с гиперболой в точке
, восстановленного в одном из фокусов до пересечения с гиперболой в точке  , т.е.
, т.е. 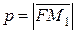 . Точка
. Точка  имеет координаты
имеет координаты  , следовательно,
, следовательно,
 , откуда
, откуда 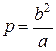 .
.
Фокальные радиусы  и
и 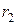 произвольной точки
произвольной точки  гиперболы в силу соотношений (10) и (11) для правой ветви гиперболы задаются формулами
гиперболы в силу соотношений (10) и (11) для правой ветви гиперболы задаются формулами
 ,
,  , (14)
, (14)
для левой –
 . (15)
. (15)
3°. Определение параболы, каноническое уравнение, исследование формы.
Пусть на плоскости заданы точка  и прямая
и прямая  , не проходящая через эту точку.
, не проходящая через эту точку.
Определение 5. Параболой называется множество точек плоскости, каждая из которых равноудалена от точки  и прямой
и прямой  . Точка
. Точка  называется фокусом параболы, прямая
называется фокусом параболы, прямая  – директрисой параболы.
– директрисой параболы.

Рис. 5
Составим уравнение параболы. Выберем прямоугольную систему координат так, что ось  проходит через фокус
проходит через фокус  перпендикулярно к директрисе
перпендикулярно к директрисе  в направлении от директрисы
в направлении от директрисы  к фокусу
к фокусу  . Начало координат возьмём в середине отрезка между фокусом
. Начало координат возьмём в середине отрезка между фокусом  и точкой пересечения оси
и точкой пересечения оси  с директрисой
с директрисой  . Пусть расстояние между фокусом и директрисой (фокальный параметр): тогда
. Пусть расстояние между фокусом и директрисой (фокальный параметр): тогда  и уравнение директрисы
и уравнение директрисы  будет иметь вид
будет иметь вид  .
.
Пусть  – произвольная точка параболы. Обозначим через
– произвольная точка параболы. Обозначим через  и назовём фокальным радиусом точки
и назовём фокальным радиусом точки  расстояние от
расстояние от  до фокуса
до фокуса  . Расстояние от точки
. Расстояние от точки  до директрисы обозначим
до директрисы обозначим  . Согласно определению параболы равенство
. Согласно определению параболы равенство

является необходимым и достаточным условием принадлежности точки  данной параболе. Так как
данной параболе. Так как

 ,
,
то соотношение
 (16)
(16)
представляет собой уравнение параболы в выбранной системе координат.
Возводя обе части равенства (16) в квадрат, получаем
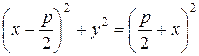 ,
,
откуда
 . (17)
. (17)
Покажем обратное: если координаты  точки
точки  удовлетворяют уравнению (17), то точка
удовлетворяют уравнению (17), то точка  лежит на параболе. Действительно, из (17) следует, что
лежит на параболе. Действительно, из (17) следует, что  . Тогда
. Тогда  . Используя это, получаем
. Используя это, получаем
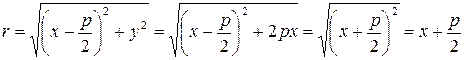 .
.
Таким образом, для того чтобы точка  с координатами
с координатами  принадлежала параболе, необходимо и достаточно, чтобы её координаты удовлетворяли уравнению (17). Уравнение (17) называется каноническим уравнением параболы.
принадлежала параболе, необходимо и достаточно, чтобы её координаты удовлетворяли уравнению (17). Уравнение (17) называется каноническим уравнением параболы.
Итак, для точки  параболы выполняется
параболы выполняется  . Так как для точек эллипса и гиперболы отношение
. Так как для точек эллипса и гиперболы отношение 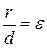 , то для параболы естественно положить эксцентриситет
, то для параболы естественно положить эксцентриситет  равным единице.
равным единице.
Из уравнения (17) видно, что все точки параболы лежат в первой и четвёртой четвертях. Ввиду того, что уравнение (17) содержит координату  только в чётной степени, то парабола симметрична относительно оси
только в чётной степени, то парабола симметрична относительно оси  , и поэтому достаточно исследовать её форму в первой координатной четверти. В этой четверти рассматриваемая парабола описывается уравнением
, и поэтому достаточно исследовать её форму в первой координатной четверти. В этой четверти рассматриваемая парабола описывается уравнением  . Функция
. Функция  является монотонно возрастающей, выпуклой вверх, так как
является монотонно возрастающей, выпуклой вверх, так как
 ,
,  .
.
Наклонных асимптот вида  для графика функций
для графика функций  в первой четверти нет (следовательно, нет их и для графика функции
в первой четверти нет (следовательно, нет их и для графика функции 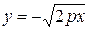 в четвёртой четверти), поскольку иначе
в четвёртой четверти), поскольку иначе
 ,
,  .
.
У параболы нет вертикальных асимптот, так как функция  непрерывна на
непрерывна на 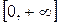 . Таким образом, парабола имеет, изображённый на рис. 6.
. Таким образом, парабола имеет, изображённый на рис. 6.

Рис. 6
Ось симметрии параболы называется её осью. Точка пересечения параболы с её осью называется вершиной параболы.
Укажем теперь геометрический смысл фокального параметра  . Для этого через фокус
. Для этого через фокус  проведём прямую, перпендикулярную к оси параболы (см. рис. 6). Уравнение этой прямой имеет вид
проведём прямую, перпендикулярную к оси параболы (см. рис. 6). Уравнение этой прямой имеет вид  . Найдём координаты точек
. Найдём координаты точек  пересечения прямой
пересечения прямой  с параболой:
с параболой:
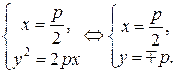
Следовательно, 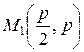 ,
, 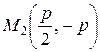 ,
, 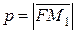 .
.
Итак, фокальный параметр  параболы равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. В этом смысле фокальный параметр
параболы равен длине перпендикуляра к оси параболы, восстановленного из фокуса до точки пересечения с параболой. В этом смысле фокальный параметр  характеризует форму параболы.
характеризует форму параболы.
4°. Директрисы эллипса и гиперболы.
Рассмотрим какой-нибудь эллипс и введём декартову прямоугольную систему координат так, чтобы этот эллипс определялся каноническим уравнением
 .
.
Предположим, что рассматриваемый эллипс не является окружностью, т.е. что  и, следовательно,
и, следовательно,  . Предположим ещё, что этот эллипс вытянут в направлении оси
. Предположим ещё, что этот эллипс вытянут в направлении оси  , т.е. что
, т.е. что  .
.
Определение 6. Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии 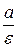 от него, называются директрисами эллипса.
от него, называются директрисами эллипса.
Уравнение директрис в выбранной системе координат имеют вид
 и
и  .
.
Первую из них мы условимся называть левой, вторую – правой.
Так как для эллипса 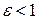 , то
, то  . Отсюда следует, что правая директриса расположена правее правой вершины эллипса; аналогично, левая директриса расположена левее его левой вершины. Эллипс вместе с директрисами изображён на рис. 7.
. Отсюда следует, что правая директриса расположена правее правой вершины эллипса; аналогично, левая директриса расположена левее его левой вершины. Эллипс вместе с директрисами изображён на рис. 7.

Рис. 7
Рассмотрим какую–нибудь гиперболу и введём декартову прямоугольную систему координат так, чтобы эта гипербола определялась каноническим уравнением
 .
.
Определение 7. Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоянии 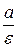 от него, называются директрисами гиперболы.
от него, называются директрисами гиперболы.
Уравнение директрис в выбранной системе координат имеют вид
 и
и  .
.
Первую из них мы условимся называть левой, вторую – правой.
Так как для гиперболы 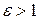 , то
, то  . Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы; аналогично, левая директриса расположена между центром и левой вершиной. Гипербола вместе с директрисами изображена на рис. 8.
. Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы; аналогично, левая директриса расположена между центром и левой вершиной. Гипербола вместе с директрисами изображена на рис. 8.

Рис. 8.
Значение директрис эллипса и гиперболы выявляется следующими двумя теоремами.
Теорема 1. Если  – расстояние от произвольной точки эллипса до какого–нибудь фокуса,
– расстояние от произвольной точки эллипса до какого–нибудь фокуса,  – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение
– расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение  есть постоянная величина, равная эксцентриситету эллипса:
есть постоянная величина, равная эксцентриситету эллипса:
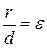 .
.
Доказательство: Предположим для определённости, что речь идёт о правом фокусе и правой директрисе. Пусть  – произвольная точка эллипса (см. рис. 7). Расстояние от
– произвольная точка эллипса (см. рис. 7). Расстояние от  до правой директрисы выражается равенством
до правой директрисы выражается равенством
 ,
,
а расстояние от  до правого фокуса даётся второй из формул (7):
до правого фокуса даётся второй из формул (7):
 .
.
Отсюда имеем:
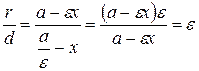 .
.
Теорема доказана. ■
Теорема 2. Если  – расстояние от произвольной точки гиперболы до какого–нибудь фокуса,
– расстояние от произвольной точки гиперболы до какого–нибудь фокуса,  – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение
– расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение  есть постоянная величина, равная эксцентриситету гиперболы:
есть постоянная величина, равная эксцентриситету гиперболы:
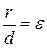 .
.
Доказательство: Предположим для определённости, что речь идёт о правом фокусе и правой директрисе. Пусть  – произвольная точка гиперболы (см. рис. 8). Нам придётся рассмотреть два случая:
– произвольная точка гиперболы (см. рис. 8). Нам придётся рассмотреть два случая:
1) Точка  находится на правой половине гиперболы. Тогда расстояние от
находится на правой половине гиперболы. Тогда расстояние от  до правой директрисы выражается равенством
до правой директрисы выражается равенством
 ,
,
а расстояние от  до правого фокуса даётся второй из формул (10):
до правого фокуса даётся второй из формул (10):
 .
.
Отсюда имеем:
 .
.
2) Точка  находится на левой половине гиперболы. Тогда расстояние от
находится на левой половине гиперболы. Тогда расстояние от  до правой директрисы выражается равенством
до правой директрисы выражается равенством
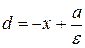 ,
,
а расстояние от  до правого фокуса даётся второй из формул (15):
до правого фокуса даётся второй из формул (15):
 .
.
Отсюда имеем:
 .
.
Теорема доказана. ■
Свойство эллипса и гиперболы, выраженное предыдущими теоремами, можно положить в основу определения этих линий. Именно
Определение 8. Геометрическое место точек, для которых расстояние  от некоторой фиксированной точки (фокуса) и расстояние
от некоторой фиксированной точки (фокуса) и расстояние  до некоторой фиксированной прямой (директрисы) находятся в постоянном отношении
до некоторой фиксированной прямой (директрисы) находятся в постоянном отношении
 , (18)
, (18)
есть эллипс, если 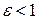 , гипербола, если
, гипербола, если 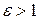 , парабола, если
, парабола, если 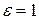 .
.
5°. Полярное уравнение эллипса, гиперболы и параболы.
Воспользуемся определением 8 для вывода полярного уравнения эллипса, гиперболы и параболы (по форме записи общее для этих трёх линий) при некотором специальном расположении полярной оси. Отметим, что в случае гиперболы это уравнение определяет линию не целиком, а только одну её ветвь.
Пусть нам дана какая–нибудь из названных линий (эллипс, гипербола или парабола, если данная линия гипербола, то мы будем рассматривать какую–нибудь одну её ветвь) и пусть  – фокус линии,
– фокус линии,  – соответствующая этому фокусу директриса (в случае гиперболы в качестве
– соответствующая этому фокусу директриса (в случае гиперболы в качестве  и
и  возьмём фокус и директрису, ближайшие к рассматриваемой ветви).
возьмём фокус и директрису, ближайшие к рассматриваемой ветви).
Введём полярную систему координат так, чтобы полюс совместился с фокусом  , а полярная ось была перпендикулярно к директрисе и направлена от неё к фокусу
, а полярная ось была перпендикулярно к директрисе и направлена от неё к фокусу  (рис. 9). Обозначим, как обычно через
(рис. 9). Обозначим, как обычно через 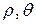 полярные координаты произвольной точки
полярные координаты произвольной точки  на линии. Чтобы вывести уравнение линии, будем исходить из соотношения (18)
на линии. Чтобы вывести уравнение линии, будем исходить из соотношения (18)
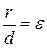 ,
,
где  – эксцентриситет линии, а
– эксцентриситет линии, а  и
и  имеют тот же смысл, что и в пунктах 1°–3°.
имеют тот же смысл, что и в пунктах 1°–3°. 

Рис. 9.
Так как полюс совмещён с фокусом  , то
, то
 . (19)
. (19)
Далее,
 . (20)
. (20)
Пусть  – точка, расположенная на линии так, что отрезок
– точка, расположенная на линии так, что отрезок  перпендикулярен к полярной оси, и
перпендикулярен к полярной оси, и  – длина отрезка
– длина отрезка  (для параболы,
(для параболы,  совпадает с её параметром).
совпадает с её параметром).
Из (18) имеем
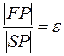 ,
,
откуда  . Но
. Но  ; следовательно,
; следовательно,
 .
.
Из последнего равенства и равенства (20) получаем:
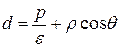 .
.
Подставляя в (18) вместо  и
и  их выражения (19) и (20), найдём:
их выражения (19) и (20), найдём:
 ,
,
откуда,
 . (21)
. (21)
Уравнение (21) является полярным уравнением эллипса, гиперболы (вернее одной ветви гиперболы) и параболы. Здесь  – фокальный параметр,
– фокальный параметр,  – эксцентриситет кривой. Уравнение (21) широко используется в небесной механике.
– эксцентриситет кривой. Уравнение (21) широко используется в небесной механике.
6°. Исследование общего уравнения второго порядка.
Пусть на плоскости задана прямоугольная определяемая репером 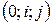 . Рассмотрим уравнение
. Рассмотрим уравнение
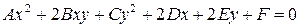 , (22)
, (22)
в котором коэффициенты  и
и 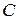 не равны нулю одновременно. Исследуем множество точек плоскости, координаты которых удовлетворяют (22), не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. При повороте базиса декартовой прямоугольной системы координат на угол
не равны нулю одновременно. Исследуем множество точек плоскости, координаты которых удовлетворяют (22), не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. При повороте базиса декартовой прямоугольной системы координат на угол 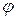 старые координаты точки
старые координаты точки  будут связаны с её новыми координатами
будут связаны с её новыми координатами  формулами
формулами
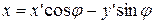 ,
,  .
.
В новых координатах уравнение (22) имеет вид

Здесь многоточием обозначены члены первой степени относительно  и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением
и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением  в преобразованном уравнении. Коэффициент при
в преобразованном уравнении. Коэффициент при  равен
равен
 .
.
Если 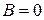 , то поворачивать систему координат не будем. Если же
, то поворачивать систему координат не будем. Если же  , то выберем угол
, то выберем угол 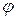 так, чтобы
так, чтобы 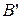 обратилось в нуль.
обратилось в нуль.
Это требование приведёт к уравнению
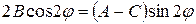 . (23)
. (23)
Если  , то
, то  , и можно положить
, и можно положить  . Если же
. Если же 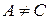 , то выбираем
, то выбираем  . После поворота системы координат на этот угол
. После поворота системы координат на этот угол 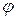 линия будет иметь уравнение
линия будет иметь уравнение
 . (24)
. (24)
Выражения для коэффициентов уравнения (24) через коэффициенты (22) легко вычисляется.
Утверждение 1. Если в уравнение (24) входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.
В самом деле, пусть, например,  . Перепишем (3) в виде
. Перепишем (3) в виде
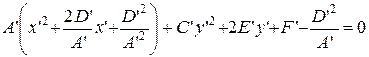 .
.
Если сделать перенос начала координат, определяемый формулами  ,
,  , то уравнение приведётся к виду
, то уравнение приведётся к виду
 ,
,
как и требовалось.
А. Далее перечислим возможные случаи уравнения (24).  , т.е. оба коэффициента отличны от нуля, то согласно предложению 1 при помощи переноса начала координат уравнение приведётся к виду
, т.е. оба коэффициента отличны от нуля, то согласно предложению 1 при помощи переноса начала координат уравнение приведётся к виду
 .
.
Возможные следующие подслучаи.
А1.  (коэффициенты
(коэффициенты  и
и  имеют один знак). Для
имеют один знак). Для 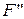 имеются следующие три возможности:
имеются следующие три возможности:
А1а. Знак 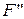 противоположен знаку
противоположен знаку  и
и  . Тогда перенесём
. Тогда перенесём 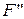 в другую часть равенства и разделим на него. Уравнение примет вид
в другую часть равенства и разделим на него. Уравнение примет вид
 ,
,
 ,
, 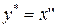 .
.
т.е. в этом случае линия является эллипсом.
А1б. Знак  совпадает с общим знаком
совпадает с общим знаком  и
и  . Тогда аналогично предыдущему мы можем привести уравнение к виду
. Тогда аналогично предыдущему мы можем привести уравнение к виду
 .
.
Этому уравнению не удовлетворяют координаты ни одной точки. Такое уравнение называется уравнением мнимого эллипса.
А1в. 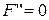 . Уравнение имеет вид
. Уравнение имеет вид
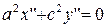 .
.
Ему удовлетворяет только одна точка  ,
,  . Уравнение называется уравнением пары мнимых пересекающихся прямых.
. Уравнение называется уравнением пары мнимых пересекающихся прямых.
А2.  – коэффициенты
– коэффициенты  и
и  имеют разные знаки. Относительно
имеют разные знаки. Относительно 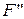 имеются следующие две возможности.
имеются следующие две возможности.
А2а. 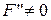 . В этом случае уравнение приводится к виду
. В этом случае уравнение приводится к виду
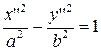 ,
,
полученная линия – гипербола.
А2б. 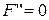 . Уравнение имеет вид
. Уравнение имеет вид
 .
.
Его левая часть разлагается на множители  и
и  и, следовательно, обращается в нуль тогда и только тогда, когда равен нулю хоть один из множителей. Поэтому эта линия состоит из двух прямых, которые пересекаются в начале координат.
и, следовательно, обращается в нуль тогда и только тогда, когда равен нулю хоть один из множителей. Поэтому эта линия состоит из двух прямых, которые пересекаются в начале координат.
Б. Если  , то, один из коэффициентов
, то, один из коэффициентов  и
и  равен нулю. Пусть
равен нулю. Пусть 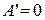 и
и  , (иначе порядок уравнения был бы равен 1, а не 2). Используя утверждение 1, риведём уравнение к виду
, (иначе порядок уравнения был бы равен 1, а не 2). Используя утверждение 1, риведём уравнение к виду
 .
.
Б1. Пусть  . Сгруппируем члены следующим образом:
. Сгруппируем члены следующим образом:
 .
.
Перенесём начало координат вдоль оси абсцисс в соответствии с формулами перехода  ,
,  . Тогда уравнение примет вид
. Тогда уравнение примет вид
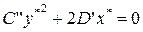 ,
,
или
 ,
,
где  . Таким образом получили параболу.
. Таким образом получили параболу.
Б2. Допустим, что  . Тогда уравнение имеет вид
. Тогда уравнение имеет вид  . Относительно
. Относительно  есть следующие три возможности:
есть следующие три возможности:
Б2а.  , т.е. знаки
, т.е. знаки  и
и 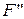 противоположны. Разделив на
противоположны. Разделив на  , приведём уравнение к виду
, приведём уравнение к виду
 .
.
Левая часть уравнения разлагается на множители  и
и  . Обращение в нуль каждого из них определяет прямую линию. Эти прямые параллельны, и, таким образом, уравнение определяет пару параллельных прямых.
. Обращение в нуль каждого из них определяет прямую линию. Эти прямые параллельны, и, таким образом, уравнение определяет пару параллельных прямых.
Б2б. 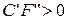 , т.е. знаки
, т.е. знаки  и
и  совпадают. Разделив на
совпадают. Разделив на  , приведём уравнение к виду
, приведём уравнение к виду
 .
.
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к такому каноническому виду, называют уравнением пары мнимых параллельных прямых.
Б2в. 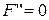 . После деления на
. После деления на  уравнение принимает вид
уравнение принимает вид
 .
.
Это уравнение эквивалентно уравнению  , и потому определяет прямую линию. Уравнение, приводящееся к этому виду, называется уравнением пары совпавших прямых.
, и потому определяет прямую линию. Уравнение, приводящееся к этому виду, называется уравнением пары совпавших прямых.
Соберём вместе полученные результаты.
Теорема 3. Пусть в декартовой системе координат задано уравнение второго порядка (24).
Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:
1)  ; 2)
; 2) 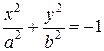 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 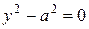 ; 8)
; 8)  ;
;
9)  .
.
В соответствии с этим существуют семь классов линий второго порядка: 1) эллипсы; 2) точки (пары мнимых пересекающихся прямых); 3) гиперболы; 4) пары пересекающихся прямых; 5) параболы; 6) пары параллельных прямых; 7) прямые (пары совпавши прямых).
Уравнению 2) мнимого эллипса и уравнению 8) пары мнимых параллельных прямых не удовлетворяет ни одна точка.
Пример 1. 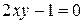
Решение. Так как  , то
, то  и формулы (4.31) имеют вид
и формулы (4.31) имеют вид
 .
.
Дата добавления: 2015-08-21; просмотров: 180 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сцена девятая | | | Примечания |