Дислокационной структуры монокристаллов

ИЗУЧЕНИЕ

Методические указания к лабораторному практикуму

по курсу «Механические свойства твердых тел» для студентов

физического факультета специализации 01.04.07

Иваново 2000

Печатается по решению методической комиссии

физического факультета

Ивановского государственного университета

Составитель:

кандидат техн. наук В.В. Новиков

(Ивановский государственный университет),

Рецензент:

кандидат техн. наук С.А. Егоров

(Ивановская государственная текстильная академия)

1. Теоретические сведения

Дислокации. В любом реальном кристалле всегда имеются дефекты строения, которые представляют собой различного рода нарушения упорядоченного пространственного расположения атомов. Дислокации относятся к линейному типу дефектов строения, они имеют малые размеры в двух измерениях и большую протяженность в третьем измерении. Дислокации бывают краевыми или винтовыми.

Краевая дислокация (рис. 1) представляет собой локализо­ванное искажение кристаллической решетки, вызванное наличием в ней «лишней» атомной полуплоскости или экстраплоскости. Наиболее простой и наглядный способ образования дислока­ции в кристалле — сдвиг (рис. 1, а). Если верхнюю часть крис­талла сдвинуть относительно нижней на одно межатомное рас­стояние, причем зафиксировать положение, когда сдвиг охватит не всю плоскость скольжения, а только часть ее АВС, то гра­ница АВ между участком, где скольжение уже произошло, и участком в плоскости скольжения, в котором скольжение еще не произошло, и будет дислокацией. Край экстраплоскости АВ представляет собой линию краевой дислокации, которая простирается вдоль плоскости скольжения (перпендикулярно к вектору сдвига t) через всю толщу кристалла (рис. 1, а).

Винтовая дислокация так же, как и краевая, образована неполным сдвигом кристалла по плоскости (рис.1, б). В отличие от краевой дислокации винтовая дислокация параллельна вектору сдвига. Винтовую дислокацию можно представить себе, как спиральное расположение атомных плоскостей решетки.

Произвольную дислокацию можно считать состоящей из отрезков, имеющих краевую и винтовую компоненты. Дислокационные линии не обрываются внутри кристалла. Они могут заканчиваться только на поверхности кристалла или на других дислокациях. Кроме того дислокации могут замыкаться сами на себя, образуя дислокационные петли.

Вектор Бюргерса. Для дислокаций характерно то, что в поперечном сечении, где имеет место существенное нарушение в периодичности и расположении атомов, размеры дефекта не велики и не превышают (3—5) а (а — период ре­шетки). При этом вокруг дислокации на протяжении нескольких межатомных расстояний возникают искажения решетки.

Характер возникающих искажений решетки можно описать с помощью вектора Бюргерса. Для этого вокруг дислокации строится контур Бюргерса, представляющий собой замкнутый контур про­извольной формы, условно выделенный в реальном кристалле путем последовательного обхода дефекта от атома к атому. Вектор, получаемый как результирующий от разности между подобными контурами Бюргерса для совершенного кристалла и для кристалла с дефектом, называется вектором Бюргерса.

Вектор Бюргерса краевой дислокации перпендикулярен линии дислокации и лежит в плоскости скольжения ABCD. Вектор Бюргерса винтовой дислокации, напротив, параллелен дислокационной линии. Если контур Бюргерса охватывает несколько дислокаций, то величина вектора Бюргерса охваченной области будет равна геометрической сумме векторов Бюргерса отдельных дислокаций.

Поля напряжений и энергия дислокаций. Энергия искажения кристаллической решетки является одной из важнейших харак­теристик дислокации любого типа.

Наиболее простой вид имеет поле напряжений винтовой дислокации. Мысленно вырежем вокруг дислокации цилиндрическую трубку, осью которой является дислокация (рис.2). Чтобы смоделировать условия напряженного состояния в зоне дислокации, деформируем трубку путем сдвига на вектор Бюргерса b по вертикали на окружности длиной 2p r. Тогда деформация сдвига равна

. (1)

Если вещество трактовать, как упругий континуум, то соответствующее напряжение сдвига

, (2)

где G — модуль сдвига.

Отметим, что данное соотношение не выполняется в области, непосредственно прилегающей к линии дислокации, так как напряжения в ней слишком велики для того, чтобы была справедливой линейная теория упругости.

Согласно теории, упругая энергия деформируемого объема определяется выражением

. (3)

Упругая энергия единицу длины трубки соответственно равна

(4)

Полная упругая энергия на единицу длины винтовой дислокации находится путем интегрирования выражения (4):

, (5)

где b – характерный размер, сравнимый с длиной вектора Бюргерса или постоянной решетки, R – расстояние, сравнимое с реальным размером кристалла.

Для краевой дислокации выражение для упругой энергии имеет вид аналогичный выражению (5):

, (6)

где n – коэффициент Пуассона (для большинства кристаллов n» 0.3). Энергия упругих напряжений, связанная с искажением кристалла дислокацией очень велика — порядка несколько эВ на одну атомную плоскость, т.е. сравнима с энергией межатомной связи в кристалле. Поэтому область поверхности кристалла, где дислокация выходит на поверхность, имеет повышенную химическую активность.

Границы зерен с малым углом разориентировки. Теория дислокаций позволила объяснить происхождение блочной структуры кристалла. Было установлено, что каждый критсалл состоит из отдельных субзерен – блоков, которые разориентированы относительно друг друга на несколько долей градуса. Граница между блоками получила название малоугловой.

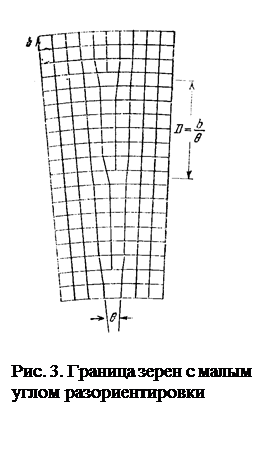
В 1939 г. Бюргерс предположил, что границы зерен между соседними блоками кристалла состоят из совокупности дислокаций. Простым примером модели границы Бюргерса может служить схема на рис. 3. Граница расположена вдоль плоскости (010) простой кубической решетки и делит кристалл на две части, для которых ось [001] является общей. Разориентировку можно описать, как малый поворот на угол J одной части кристалла относительно другой. Граница состоит из совокупности краевых дислокаций расположенных на расстоянии

D = b/J, (7)

где b – длина вектора Бюргерса.

Изучение субструктуры имеет большое значение, так как размеры блоков и угол их разориентировки влияют на многие свойства кристалла в целом. Например, имеет место повышенная диффузионная проводимость по границам субзерен и др. Это связано с наличием сильных полей напряжений и повышенным энергетическим состоянием твердого тела в области границ субзерен из-за большого скопления дислокаций.

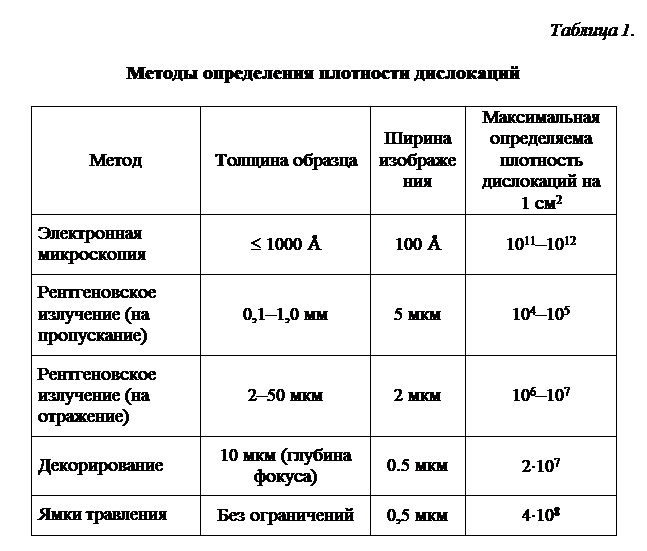
Плотность дислокаций. Плотность дислокаций определяется как число дислокационных линий, пересекающих единичную площадку внутри кристалла. Возможные значения плотности дислокаций простираются от 10²–10³ см^–2 в наиболее совершенных кристаллах германия и кремния до 10¹¹–10¹² см^–2 в сильно деформированных металлических кристаллах. Сравнительная характеристика методов, используемых для определения плотности дислокаций представлена в табл. 1.

В литом или в отожженном кристаллах дислокации либо сосредоточены на границах с малым углом разориентировки, либо образуют трехмерные сетки.

Процесс возникновения дислокаций при кристаллизации расплава и их способность сохраняться даже после длительного отжига (нагрев и медленное охлаждение) до конца не понят. Дислокации не являются термодинамически равновесными дефектами, поэтому их образование связано с неравновесными процессами внутри кристалла. Наиболее вероятно они возникают при осаждении и слиянии вакансий (вакансия — дефект, вызванный отсутствием атома в решетке), т.к. если в кристалле нет дислокаций, то он будет пересыщен вакансиями.

Процесс возникновения дислокации из скопления вакансий может быть описан, например, следующим образом. Вакансии объединяются в виде дискообразных полостей. Далее полость захлопывается, в результате образуется дислокационная петля. Далее петля растет по мере поглощения других вакансий.

При пластической деформации кристаллов дислокации обладают способностью к скольжению и размножению. Механизм пластической деформации путем скольжения обусловлен движением и выходом на поверхность дислокационных линий. При этом количество дислокаций не уменьшается, а, напротив, возрастает. Например, для металлических кристаллов при деформации плотность дислокаций увеличивается с 10⁸ до 10¹¹ см^–2, т.е. в 1000 раз. Плотность дислокаций, локализация дислокаций в объеме оказывает большое влияние на механические и другие свойства кристалла.

2. ПРАКТИЧЕСКИЕ СВЕДЕНИЯ

Приборы, материалы, инструмент: пластинки монокристалла полупроводника (кремния, германия и др.), набор травителей, металлографический микроскоп МИМ-7, объект-микрометр.

Метод избирательного травления. Одним из способов обнаружения дислокация в кристаллах является избирательное травление, основанное на существовании соответствия между ямками травления, образующимися при травлении поверхности кри­сталла, и выходом дислокация на эту поверхность (табл.1).

Доказательства, свидетельствующие о соответствии ямок травления дислокациям, следующие:

1. Число и расположение ямок на поверхности остаются сравнительно постоянными после повторных травлении в том же или дру­гих травителях. При длительном травлении ямки углубляются и растут, оставаясь остроконечными.

2. Ямки травления, полученные на одной половине расколотого образца, являются зеркальным отражением ямок на другой.

Химическое растворение кристалла начинается с дефектных мест решетки, обладающих повышенной свободной энергией. Формирование ямки травления на плоскости начинается, с того момента, когда один из атомов (ионов) переходит в раствор, образуя центр растворения (рис. 4 а, б). В последующие моменты времени удаление атомов (ионов) будет происходить со ступенек, т.к. атонн на ступеньках связаны с решеткой слабее (рис. 4 в). В результате элементарные ступеньки будут перемещаться в танген­циальном направлении. Внутри полученной фи­гуры растворения может возникнуть новый центр растворения и образуется ступенька 2, затем 3 и т.д. ( рис. 4, г).

Если к поверхности кристалла подходит дислокационная линия, центры растворения будут преимущественно образовываться на дислокационной линии, из-за того, что вблизи дислокации кристалл будет обладать повышенной энергией. Фигура травления при этом будет иметь форму, показанную на рис. 4, д.

Травление поверхности называется избирательным, если центры растворения образуются только на выходах дислокаций. Избирательное травление реализуется только при использовании специальных травителей (табл. 2). Для каждого кристалла подбирается свой индивидуальный травитель.

Скорость образования центров растворения на дислокации зависят от химического потенциала дислокационной линии и упругого поля дислокации. Последнее зависит от величины и направления вектора Бюргерса, количества и характера примесей, скопившихся вблизи линии дислокации и др. Все эти факторы будут оказывать влияние на глубину фигур травления. Можно ожидать различной травимости краевых и винтовых дислокаций.

Скорость избирательного травления различных граней кристалла различна. Плоскости с низкими значениями индексов Миллера, благодаря большой плотности атомов, обладают невысокой скоростью растворения. Грани кристалла с высокими индексами можно представить состоящими из большого числа ступенек, образованных плоскостями с малыми индексами. Движение этих ступенек будет стирать центры растворения на дислокациях.

Из-за анизотропии скоростей растворения травитель растворяет грань неравномерно. Поэтому ямка травления имеет определенную форму, а именно, симметрия фигуры травления отвечает симметрии грани кристалла. Тогда, если известен тип кристаллической решетки исследуемого образца, анализ элементов симметрии грани позволяет определить кристаллографическую ориентацию грани — ее символы Миллера.

При исследовании поверхности методом избирательного травления решающую роль в достоверности информации играет правильная подготовка этой поверхности. Срезы кристалла обрабатываются в следующей последовательности. Сначала поверхность шлифуется абразивными порошками убывающей степени дисперсности. Затем механически полируется до зеркальной чистоты. Наконец, полируется химически для того, чтобы снять дефектный слой, который возникает при механической обработке.

Определение плотности дислокаций. В связи с малыми размерами ямок травления анализ поверхности осуществляют с помощью металлографических микроскопов. В работе для наблюдения используется вертикальный металлографический микроскоп МИМ-7, инструкция по работе с которым прилагается.

Набор сменных объективов и окуляров позволяет при визуальном наблюдении увеличивать изображение от 60 до 1440^´. При работе с объективами, чье фокусное расстояние меньше F = 8.2, необходимо использовать иммерсионные масла, которые наносятся на фронтальную линзу объектива, а столик с объектом опускается до соприкосновения с иммерсионным маслом.

Для определения плотности дислокаций необходимо подсчитать количество ямок травления на некоторой заданной площади образца. Один из методов подсчета состоит в том, что подсчет ведется с помощью квадрата или прямоугольника. При таком методе подсчета те ямки, которые находятся в пределах контура, должны учитываться полностью. Те ямки, которые рассекаются линией контура, учитываются в половинном количестве (коэффициент учета 0,5). Ямки, которые попали на вершины контура, учитываются в количестве ¹/₄ (коэффициент учета 0,25). Приведенное количество ямок X определяется по формуле

X= Z + 0,5 W + 0,25 U, (8)

где Z – количество ямок внутри контура, W – количество ямок, пересеченных прямыми линиями контура, U – количество угловых ямок.

Теперь, если известна площадь поверхности, на которой производился подсчет ямок, то плотность дислокаций можно найти из отношения числа ямок к данной площади.

Плотность дислокаций — величина статистическая. Она различна для различных участков поверхности образца. Поэтому для получения надежного значения плотности дислокаций, характеризующей всю исследуемую поверхность в целом, необходимо подсчитать ямки травления на нескольких различных участках поверхности, а результат усреднить. Закон распределения плотности дислокаций описывается функцией нормального распределения. В большинстве случаев достаточно подсчитать ямки травления на 10–20 участках.

3. ВЫПОЛНЕНИЕ РАБОТЫ

Дата добавления: 2015-08-21