Описание метода

ИЗУЧЕНИЕ ИЗОТЕРМИЧЕСКОГО ПРОЦЕССА РЕАЛЬНОГО ГАЗА

Цель работы: изучить зависимость давления реального газа от объема при постоянной температуре, определить упругость насыщенного пара.

Оборудование: стеклянная трубка с исследуемым веществом, манометр, насос.

Описание метода

Газы не идеальны. При сравнительно высоких давлениях и низких температурах их состояние не подчиняется уравнению Менделеева–Клапейрона. Из большого числа уравнений состояния реальных газов уравнение Ван-дер-Ваальса отличается тем, что оно описывает переход газа в жидкое состояние и что поправки, введенные в уравнение состояния идеального газа Менделеева–Клапейрона, имеют физический смысл. Для одного моля оно имеет вид

, (1)

где – учет собственного объема молекул, 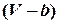– объем, доступный для движения молекул; 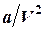– добавочное давление, обусловленное взаимным притяжением молекул. Слой молекул около стенки сосуда притягивается к внутренним молекулам под действием сил Ван-дер-Ваальса. В результате давление в газе выше, чем на стенку. Сила добавочного давления пропорциональна произведению числа молекул (или их концентрации ) у поверхности и внутри газа. Так как , то добавочное давление обратно пропорционально квадрату объема газа.

Изотермы Ван-дер-Ваальса представлены на -диаграмме (рис. 1). Среди них есть особая изотерма при температуре, равной так называемой критической . Если , то сжатием газ нельзя перевести в жидкое состояние. В этой области состояние газа удов­лет­во­ри­тель­но описывается урав­нением Менделеева–Клапейрона.

При температурах меньше критической газ из состояния ненасыщенного пара можно сжатием перевести в жидкое состояние. По мере уменьшения объема (рис. 1) давление пара вначале возрастает и при давлении, равном упругости насыщенного пара начинается конденсация (рис. 1, т. А).

Обычно -образная часть изотермы, соответствующая метастабильным состояниям перенасыщенного пара и перегретой жидкости, экспериментально не реализуется. Поэтому изотерма представляет собой горизонтальный участок, конденсация газа происходит при постоянном давлении . После полной конденсации (т. В) дальнейшее сжатие приводит к резкому повышению давления, так как жидкости мало сжимаемы.

Колоколообразная область на -диаграмме (рис. 1) соответствует области совместного существования жидкости в равновесии со своим насыщенным паром. Вершина колоколообразной кривой соответствует особому состоянию вещества – критическому, при котором физические свойства жидкости и насыщенного пара одинаковы, между ними исчезает граница раздела, теплота парообразования равна нулю.

Область на -диаграмме слева от колоколообразной кривой и под критической изотермой соответствует жидкому состоянию, справа – состоянию ненасыщенного пара, а над критической изотермой – состоянию идеального газа.

В данной работе в качестве исследуемого вещества используется пентан С₅Н₁₀. Критическая температура пентана 196 °С и поэтому при комнатной температуре он может находиться как жидком, так и в газообразном состоянии в зависимости от давления.

Дата добавления: 2015-08-21