Жесткость шпиндельного узла

Радиальная жесткость определяется из зависимости 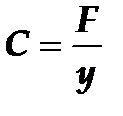, где F – радиальная сила, а y – радиальное перемещение.

Радиальное перемещение переднего конца шпинделя можно представить как сумму .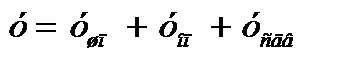

Радиальное перемещение переднего конца шпинделя:

,

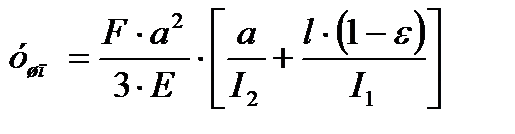где l – расстояние между опорами, a - длина переднего конца шпинделя, Е – модуль сдвига, I₁ и I₂ – осевые моменты инерции межопорной части и конца.

Радиальное перемещение за счёт податливости опор:

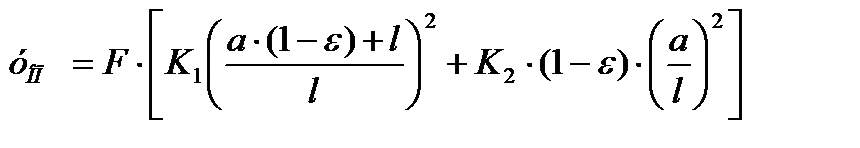, где К₁ и К₂ – податливость передней и задней опор.

Радиальное перемещение за счёт сдвига шпинделя:

,

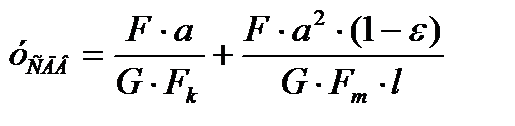где 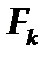- площадь сечения переднего конца шпинделя, 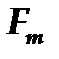- площадь сечения межопорной части шпинделя, G – модуль сдвига.

Осевые моменты инерции:

Переднего конца:

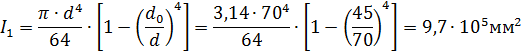
Межопорной части:

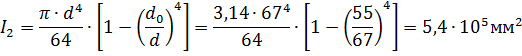
Тогда радиальная жесткость шпиндельного узла:

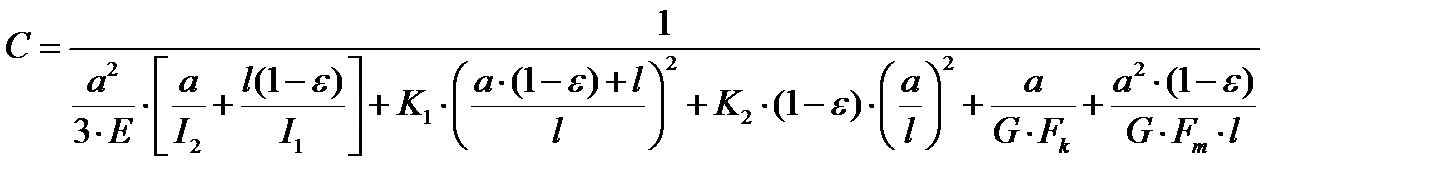
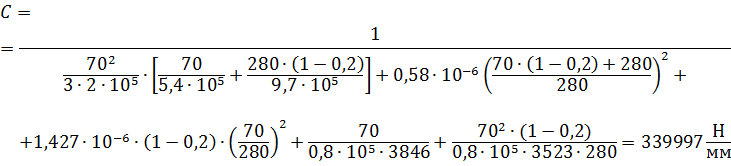
9 Расчёт оптимального межопорного расстояния.

Уравнение податливости:

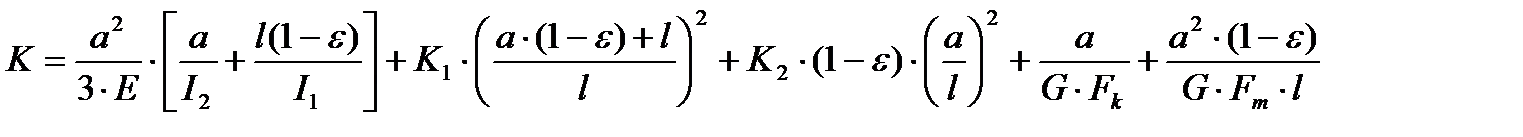
Для определения оптимальной длины необходимо найти точку перегиба уравнения податливости. Для этого уравнение податливости дифференцируем по dl, приравниваем к нулю и решаем относительно l.

Получим

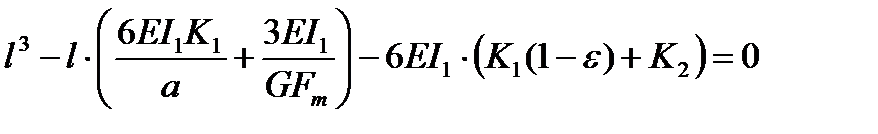
Введя обозначения, получим

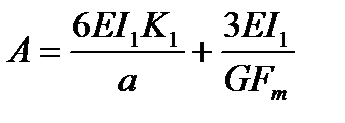
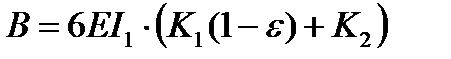
Решаем уравнение аналитически. Применяя формулу:

l_опт=U+V, где

, .

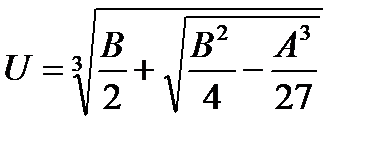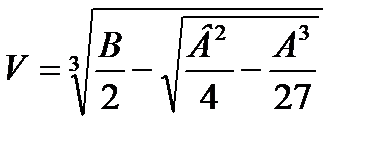Тогда оптимальное межопорное расстояние равно:

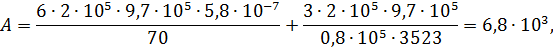
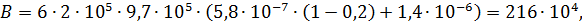
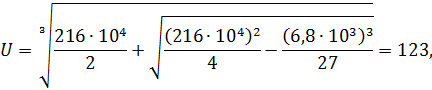
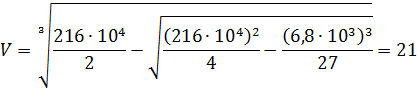
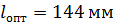. Конструктивно принимаем .

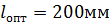Дата добавления: 2015-08-21