Расчет передаточной функции. Курсовая работа

Курсовая работа

по дисциплине

ОСНОВЫ ТЕОРИИ ЦЕПЕЙ

Вариант 3

Выполнил(а)

Проверил(а)

САНКТ-ПЕТЕРБУРГ

Содержание

1. Расчет цепи с управляемым источником в установившемся режиме. 3

1.1. Расчет передаточной функции. 3

1.2. Построение АЧХ и ФЧХ.. 5

1.3. Определение устойчивости. 6

1.4. Определение реакции цепи на периодическое негармоническое воздействие 7

1.4.1. Расчет и построение входного напряжения. 7

1.4.2. Расчет и построение выходного напряжения. 9

2. Расчет переходных процессов в цепи. 12

2.1. Определение переходной и импульсной функций. 12

2.2. Построение переходного процесса при ступенчатом входном воздействии 14

2.3. Расчет переходного процесса при импульсном воздействии. 15

3. Выводы по работе. 16

Список использованной литературы.. 17

Расчет цепи с управляемым источником в установившемся режиме

Расчет передаточной функции

Вариант

*

Рисунок

R1, кОм

R2, кОм

R3, кОм

R4, кОм

R5, кОм

C1, нФ

C2, нФ

C3, нФ

C4, нФ

C5, нФ

2,5

R₇ = R_H = 1 кОм, α_U = 50000.

Рис. 3

Составим схему замещения (рис.1.1).

Так как имеется отрицательная обратная связь с нулевым сопротивлением, то здесь имеем неинвертирующий повторитель напряжения (аттенюатор):

U₂₀ = U₃₀. Его коэффициент передачи H_U2(p) = U₂(p)/U₂₀(p) = U₂₀(p)/E₁(p) ≈ 1.

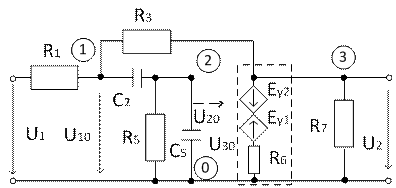
Рис. 1.1.

В расчетной схеме ОУ представляется ветвью с управляемыми источниками напряжения:

E_y1(p) = α_U1U₂₀(p); E_y2(p) = α_U2U₃₀(p)

Далее принимаем α_U1=α_U2=α_U2=α.

Найдем коэффициент передачи до ОУ H_U1

Расчет цепи методом узловых напряжений.

Граф цепи с управляемым источником напряжения изображен на рис. 1.2, где принято:

E₁(p) = U₁(p), U₂(p) - входное и выходное напряжение;

y₁(p), y₂(p), y₃(p), y₄(p), y₅(p), y₆(p), y₇(p) - проводимости вет­вей;

Рис. 1.2.

Для упрощения записи проводим замены U_i(p) → U_i, y_i(p) → y_i.

Система уравнений по методу узловых напряжений

узел 1: U₁₀∙y₁₁-U₂₀∙y₁₂ –U₃₀∙y₁₃ = E₁∙y₁

узел 2: U₂₀∙y₂₂-U₁₀∙y₁₂ = 0

узел 3: U₃₀∙y₃₃-U₁₀∙y₁₃ = (E_y1-E_y2)∙y₆ = (αU₂₀-αU₃₀)∙y₆

Здесь принято:

у₁₁ = у₁+ у₂ + у₃ - сумма прово­димостей ветвей, сходящихся в узел 1;

у₂₂ = у₃ + у₅ - сумма проводимостей ветвей, сходящихся в узел 2;

у₃₃ = у₂ + у₆ + у₇ - сумма проводимостей ветвей, сходящихся в узел 3;

у₁₂ = у₃ - проводимость ветвей между узлами 2 и 3

у₁₃ = у₂ - проводимость ветвей между узлами 1 и 3

у₁ = 1/R₁; у₂ = 1/R₂; у₃ = C₃p; у₅ = C₅p+1/R₅; у₆ = 1/R₆; у₇ = 1/R₇ - проводимости ветвей.

Искомая зависимость - это передаточная функция по напряжению

H_U(p) = H_U1(p)∙H_U2(p) = H_U1(p) = U₂(p)/U₁(p) = U₃₀(p)/E₁(p)

Решаем систему

U₂₀= U₁₀∙y₁₂/y₂₂

U₁₀ = (E₁∙y₁+U₂₀∙y₁₂+U₃₀∙y₁₃)/y₁₁

U₁₀ = (E₁∙y₁+U₁₀∙y₁₂∙y₁₂/y₂₂+U₃₀∙y₁₃)/y₁₁

U₁₀ = (E₁∙y₁+U₃₀∙y₁₃)/y₁₁+ U₁₀∙y₁₂²/(y₂₂∙y₁₁)

U₁₀(1-y₁₂²/(y₂₂∙y₁₁)) = (E₁∙y₁+U₃₀∙y₂)/y₁₁

U₁₀ = (E₁∙y₁+U₃₀∙y₂)/(y₁₁-y₃²/y₂₂)

U₃₀∙y₃₃-(E₁∙y₁+U₃₀∙y₂)∙y₁₃/(y₁₁-y₃²/y₂₂) = (αU₂₀-αU₃₀)∙y₆

Получаем

Числитель в знаменатель выражения делим на α

Микросхема серии К140УД имеет значительный коэффициент уси­ления по напряжению α ≥ 30∙10³, принимаем α → ∞. Находим

Отсюда находим искомую передаточную функцию по напряже­нию

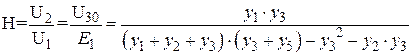
Заменяем проводимости ветвей элементами электрической цепи в операторном виде, получаем

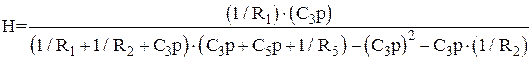
Подставим значения параметров цепи.

Коэффициенты при р²

С₅∙R₁ = 2,5∙40∙10^-6 = 100∙10^-6

при р

(1/R₁+1/R₂)∙C₅/(C₃/R₁)+(C₃/R₅)/(C₃/R₁)-(C₃/R₂)∙(1/R₁+1/R₂)∙(1/R₅)/(C₃/R₁) =1,75

при р⁰

(1/R₁+1/R₂)∙(1/R₅)/(C₃/R₁) = 7500

Получим

Н = р/(100∙10^-6р²+1,75р+7500)

Дата добавления: 2015-08-21