Колебательного контура».

Задание

На лабораторную работу №6

по дисциплине «Теория электрических цепей»

Исследование последовательного

колебательного контура».

Цель работы: получение навыков расчёта и экспериментального исследования электрических цепей, в которых наблюдается резонанс напряжений.

Используемое оборудование и ПО:

- учебная установка «Теория линейных электрических цепей»;

- программный пакет для математического моделирования (MathCAD, Excel, MatLab);

- программный пакет для схемотехнического моделирования (MicroCAP, EWB).

В последовательном колебательном контуре возникает явление резонанса напряжений. Частоту f₀ , на которой наблюдается резонанс напряжений, называют резонансной.

На рис. 1 изображена схема последовательного колебательного контура с реактивными элементами L и С и резистивным сопротивлением R.

Рис. 1. Последовательный колебательный контур

Комплексное сопротивление контура на частоте ω:

Z = R + jX = R + j(ωL – 1 / ωC).

Ток в контуре:

I = U / Z = U / (R + jX).

Фазовый сдвиг между током и приложенным напряжением:

φ = arctg [(ωL – 1 / ωC) / R] = arctg (X / R).

Резонансная частота

На резонансной частоте ω₀:

- комплексное сопротивление носит чисто активный характер Z ₀ =R;

- ток совпадает по фазе с приложенным напряжением φ₀ = 0;

- ток достигает максимального значения, равного I₀ = U / R;

- реактивные сопротивления контура равны друг другу

.

Величина ρ носит название характеристического сопротивления контура. Резонансные свойства контура характеризуются добротностью контура Q:

.

Добротность Q показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение. Величина, обратная добротности, называется затуханием контура:

.

Выходное напряжение контура может сниматься с различных элементов контура. В соответствии с этим представляет интерес коэффициент передачи цепи по напряжению относительно элементов R, C и L. АЧХ и ФЧХ последовательного контура:

Важная характеристика колебательного контура – полоса пропускания. Абсолютной полосой пропускания называют диапазон частот, в пределах которого коэффициент передачи уменьшается в раз по сравнению с максимальным, т.е. составляет 0,707 от максимального значения. Абсолютная полоса пропускания:

∆f=f_В – f_Н ,

где f_В и f_Н - верхняя и нижняя граничные частоты.

Относительная полоса пропускания:

Абсолютную и относительную полосу пропускания можно выразить через добротность и затухание:

.

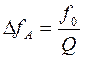
I. Расчетная часть (математическое моделирование)

Для последовательного колебательного контура, у которого L = L1 мГн, C = C1 нФ, R=R1 Ом, рассчитайте собственную круговую ω₀ и циклическую f₀ частоты, добротность Q, характеристическое сопротивление ρ и полосу пропускания ∆f на уровне 0,707. Исходные данные по вариантам приведены в таблице 1. Результаты расчетов занесите в таблицу 1 и третий столбец таблицы 3.

Таблица 1

Расчетные параметры последовательного колебательного контура

Вар-т	L1, мГн	C1, нФ	R1, Ом	ω0, рад/с	f0, кГц	Q	ρ, Ом	∆fA 0,707

Дата добавления: 2015-08-21