
Читайте также:
|
Рассчитать амплитудный корректор по заданной характеристике рабочего ослабления (затухания) канала связи ак.
Исходные данные:
Вид характеристики и частотный интервал, в котором ее следует, корректировать определяются данными, приведенными в таблице 2:
Таблица 2
| f, кГц | 1.5 | 2.5 | 3.5 | 4.5 | ||||
| ак, дБ | 10,2 | 11,4 | 12,4 | 13,3 | 14,1 | 14,6 | 15,2 | 15,6 |
Суммарная характеристика рабочего ослабления арез цепи, полученной путем каскадного соединения канала связи и амплитудного корректора, должна отклоняться в заданном частотном интервале от постоянного, частотно-независимого значения на величину  , не превышающую 1,5 дБ.
, не превышающую 1,5 дБ.
Корректор должен быть рассчитан на равные с двух сторон нагрузочные сопротивления R1=R2=1000/M=1000/1=1000Ом ивыполнен в видеT- образной семы постоянного водного напряжения.
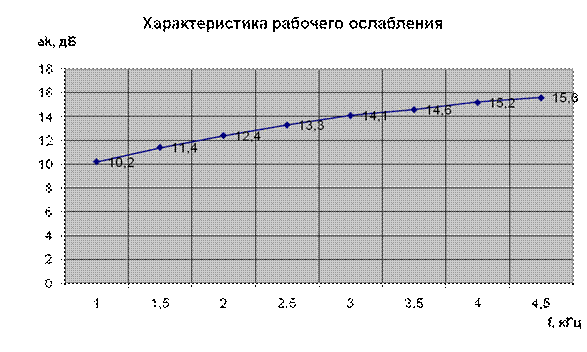
Рисунок 8
Определим требуемую характеристику рабочего ослабления корректора атр. Для этого зададимся результирующей характеристикой.
 дБ,
дБ,
где ак max – максимальное значение ослабление канала в диапазоне от 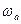 до
до  .
.
Вычислим требуемое ослабление корректора:
 = 20,28 – 15,6 = 4,68 дБ
= 20,28 – 15,6 = 4,68 дБ
Для удобства последующих расчетов целесообразно пронормировать частоты  относительно некоторой фиксированной частоты
относительно некоторой фиксированной частоты 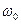 .
.
 с-1
с-1
Требуемую характеристику рабочего ослабления корректора атр представим графически в зависимости от нормированной частоты  и покажем пределы допустимого отклонения
и покажем пределы допустимого отклонения 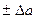 .
.
И составим таблицу 3.
Таблица 3
| f,кГц | 1.5 | 2.5 | 3.5 | 4.5 | ||||

| 0,364 | 0,545 | 0,727 | 0,909 | 1,091 | 1,273 | 1,455 | 1,636 |
| атр, дБ | 10,08 | 8,88 | 7,88 | 6,98 | 6,18 | 5,68 | 5,08 | 4,68 |

Рисунок 9
Решим аппроксимационную задачу, т.е. найдем функцию  , представляющую собой амплитудно-квадратичную характеристику
, представляющую собой амплитудно-квадратичную характеристику  , которая обеспечивает точность характеристики рабочего ослабления рассчитываемого корректора. Так как требуемая характеристика ослабления корректора с ростом частоты убывает, то функцию
, которая обеспечивает точность характеристики рабочего ослабления рассчитываемого корректора. Так как требуемая характеристика ослабления корректора с ростом частоты убывает, то функцию  следует искать в виде:
следует искать в виде:

Функция  содержит два неизвестных коэффициента: А и B. Т.к. амплитудно-квадратичная характеристика корректора связана с характеристикой ослабления соотношением:
содержит два неизвестных коэффициента: А и B. Т.к. амплитудно-квадратичная характеристика корректора связана с характеристикой ослабления соотношением:

поэтому для отыскания двух неизвестных коэффициентов  необходимо составить два уравнения вида:
необходимо составить два уравнения вида:
 ; i=1,2
; i=1,2
для двух выбранных узлов интерполяции на частотах  и
и 
Выберем:
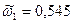 , акор=8,88 дБ
, акор=8,88 дБ
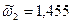 , акор=5,08 дБ
, акор=5,08 дБ
Составляем два уравнения

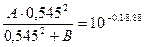




Решаем их относительно А и В, находим  ,
,  . Следовательно, искомая функция:
. Следовательно, искомая функция:

Полученная функция удовлетворяет условию реализуемости, так как А>0, B>0, и кроме того А  1.
1.
Убедившись, что функция  реализуема, проверим удовлетворяет ли она точности коррекции, т.е. выполняется на всех заданных частотах в интервале от
реализуема, проверим удовлетворяет ли она точности коррекции, т.е. выполняется на всех заданных частотах в интервале от 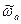 до
до  условие:
условие:
 дБ
дБ
Для этого подставляем в формулу  функцию
функцию  .
.
Представим требуемую характеристику рабочего ослабления корректора в виде таблицы 4:
Таблица 4
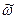 , 1/с , 1/с
| 0,363 | 0,545 | 0,727 | 0,909 | 1,091 | 1,273 | 1,455 | 1,636 |
| атр, дБ | 10,08 | 8,88 | 7,88 | 6,98 | 6,18 | 5,68 | 5,08 | 4,68 |
| акор, дБ | 11,569 | 8,91 | 7,374 | 6,425 | 5,807 | 5,388 | 5,092 | 4,878 |

| 1,489 | 0,03 | 0,506 | 0,555 | 0,373 | 0,292 | 0,012 | 0,198 |
В результате расчета видим, что неравенство  дБ выполняется.
дБ выполняется.
На графике покажем, что заданная точность коррекции выполняется на всех заданных частотах.

Рисунок 10
Определим нормированную передаточную функцию 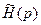 . Для нашей функции
. Для нашей функции  соответствует передаточная функция
соответствует передаточная функция  , где
, где  ,
,  ,
,

Теперь синтезируем схему корректора и вычислим параметры элементов.
Для передаточной функции вида:
 ,
,
полагая, что  , получим выражение для нормированных сопротивлений
, получим выражение для нормированных сопротивлений  и
и 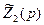 перекрытой Т-образной схемы:
перекрытой Т-образной схемы:
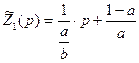
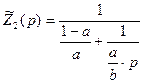


 Схема корректора показана на рисунке:
Схема корректора показана на рисунке:
Рисунок 11
Нормированные параметры элементов схемы могут быть вычислены по формулам:

Для вычисления номинальных значений параметров воспользуемся формулами:
 мГн
мГн
 Ф
Ф
 Ом
Ом
 Ом
Ом
Дата добавления: 2015-08-21; просмотров: 393 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Расчет ARC-фильтра | | | Тема 3. Анализ электрических цепей. Основные теоремы. |