
|
Читайте также: |
Форми представлення чисел в ЕОМ. Діапазони представлення чисел.
1. Форми представлення даних
Найменша одиниця інформації – двійковий розряд (0 або 1), що отримав назву біт. Для представлення символів в ЕОМ використовується байт (8 біт).
Найменшою структурною одиницею інформації, що адресується, в сучасних ЕОМ прийнятий байт і, відповідно, використовується байтова організація інформації в оперативній пам'яті.
Для представлення в ЕОМ алфавітно-цифрової інформації зазвичай застосовується машинне слово, що являє сукупність символів, яка витягується з оперативної пам'яті або записується в неї за одне звернення. Машинне слово зазвичай містить ціле число байтів, які утворюються послідовно, починаючи з нуля.
У ЕОМ і мікроЕОМ як операнди використовуються такі формати даних: байт, півслово, слово, подвійне слово і поле – інформаційна одиниця змінної довжини, але|та| не більше 256 байт (рис. 1).
0 7 8 15 16 31 32 63

байт
півслово
слово
подвійне слово
Рис. 1. Формати даних
Для мікропроцесорів і мікроЕОМ застосовуються формати даних з|із| довжиною слова 4, 8, 12, 16, 32 і 64 біта. Побайтова організація інформації в пам'яті ЕОМ забезпечує інформаційну сумісність форматів даних між різними мікропроцесорами і мікроЕОМ.
Форми представлення чисел
При розміщенні оброблюваної інформації в ЕОМ слід враховувати необхідність контролю її обробки і адресації у комірці оперативної пам'яті. Це викликає певні вимоги до організації розрядної сітки ЕОМ. Під розрядною сіткою ЕОМ розуміють кількість розрядів, необхідних для розміщення у комірці оперативної пам'яті повного машинного слова. Для кожного типа ЕОМ вона має чітко обмежену кількість розрядів.
У ЕОМ використовуються дві форми представлення чисел в розрядній сітці:
– з|із| фіксованою комою (крапкою|точкою|) (ФК);
– з|із| плаваючою комою (крапкою|точкою|) (ПК).
Подання з|із| ФК – це природна форма представлення числа, яка характеризується тим, що положення|становище| його коми в розрядній сітці завжди залишається постійним (фіксується), незалежно від величини самого числа. Зазвичай|звично| кома фіксується перед старшим або після|потім| молодшого розряду. Якщо кома фіксується перед старшим розрядом, то числа в ЕОМ представляються як правильні дроби (рис.2 а), якщо після|потім| молодшого – як цілі числа (рис.2 б).
Для кодування знаку числа використовується знаковий розряд (на рис. 2 – нульовий). У цьому розряді 0 відповідає плюсу, а 1 – мінусу. На розрядній сітці вказано вагу кожного розряду. Найбільше додатне число, яке можна представити у розрядній сітці 32-розрядної ЕОМ, дорівнює:

 0, 111…11 = 1-2-31 ,
0, 111…11 = 1-2-31 ,
31 одиниця
а найменше число –
 0, 000…001 = 2-31 .
0, 000…001 = 2-31 .
30 нулів|нуль-елементів|
 Рис. 2. Представлення числа в ЕОМ
Рис. 2. Представлення числа в ЕОМ
У розрядній сітці такої ЕОМ можуть бути представлені числа в діапазоні від - (1-2-31) до -2-31 і від +2-31 до (1-2-31), що відповідає діапазону абсолютних десяткових чисел приблизно від (1-10-9) до 10-9.
Числа |х|<2-31 не можуть бути зображеними у розрядній сітці і приймаються рівними нулю (число виходить за розрядну сітку праворуч). Такий нуль називається машинним.
Всі числа |х|≥1 також не можуть бути представлені|уявляти| в прийнятій розрядній сітці. Таке число «виходить з|із| сітки ліворуч» (переповнення розрядної сітки) і його старші розряди втрачаються|розгублюють|, результати обчислень|підрахунків| виявляються|опиняються| невірними. Тому при переповненні зазвичай|звично| відбувається|походить| автоматична зупинка машини або формується сигнал переривання програми.
Якщо кома фіксована праворуч від молодшого розряду, розрядна сітка дозволяє представляти додатні і від’ємні числа (цілі), модуль яких 1 ≤ х ≤ 231 -1, що відповідає діапазону абсолютних десяткових чисел приблизно від 1 до 109, а також включає 0.
При виконанні на ЕОМ обчислень|підрахунків| необхідно, щоб|аби| всі початкові, проміжні, що з’являються в процесі обчислень,|підрахунку| і кінцеві|скінченні| дані не виходили за діапазон чисел, що можуть бути подані в даній розрядній сітці. Інакше в обчисленнях|підрахунках| можуть виникнути грубі помилки. Для цього під час програмування завдання|задачі| дані для обчислень|підрахунках|, беруться з|із| відповідними масштабними коефіцієнтами.
Використання представлення чисел у ФК дозволяє спрощувати схеми ЕОМ, підвищувати їх швидкодію, але|та| створює труднощі при програмуванні. Формати з|із| ФК використовувались у перших ЕОМ.
У даний час|нині| представлення чисел з|із| ФК використовується як основне і єдине лише в порівняно невеликих за своїми обчислювальними можливостями|спроможностях| масштабах, вживаних для управління технологічними процесами і обробки вимірювальної інформації в реальному масштабі часу.
В ЕОМ, призначених для вирішення широкого кола обчислювальних завдань|задач|, основним є представлення чисел з|із| плаваючою комою, оскільки воно не вимагає масштабування даних. У комп’ютерах форма з|із| ПК використовується при переповненні чисел ФК. Причому переведення|переказ| виконується автоматично, за підпрограмою (мікропрограмою).
Часто поряд з|поряд із| ПК використовується і форма з|із| ФК, оскільки операції з|із| такими числами виконуються за менший час. При цьому в більшості випадків формат чисел з|із| ФК служить для представлення цілих двійкових чисел (кома фіксується праворуч від молодшого розряду числа) і виконання операцій над ними, що, зокрема, необхідно для операцій над кодами адрес (операції індексної арифметики).
Представлення числа з|із| ПК у загальному|спільному| випадку має вигляд|вид|:
 , (1.13)
, (1.13)
де m – мантиса числа N, | m | < 1;
p – порядок числа;
r – основа с/ч;
r±p – характеристика числа N.
Це представлення числа називається також напівлогарифмічним, оскільки частина числа – характеристика (rp) – подається в логарифмічній формі.
Мантиса числа m є правильним дробом.
Порядок p, який може бути додатним або від’ємним числом, визначає положення коми в числі N.
Наприклад,

Для двійкових чисел 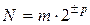 .
.
Нехай|нехай|, наприклад, розрядна сітка ЕОМ включає 32 розряди, а число  зображають двійковим словом:
зображають двійковим словом:  , якому відповідає формат даних, показаний на рис. 3.
, якому відповідає формат даних, показаний на рис. 3.

Рис. 3 Формат даних
Розряди  використовуються для представлення порядку|ладу| p, при цьому розряд
використовуються для представлення порядку|ладу| p, при цьому розряд  змальовує|зображає| знак порядку|ладу|, а розряди
змальовує|зображає| знак порядку|ладу|, а розряди  - модуль порядку|ладу|. Наприклад, порядок|лад| «-5» представляється у вигляді 1000101.
- модуль порядку|ладу|. Наприклад, порядок|лад| «-5» представляється у вигляді 1000101.
Решта розрядів 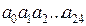 відводяться під зображення мантиси m. Розряд
відводяться під зображення мантиси m. Розряд 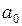 служить для представлення знаку мантиси, а розряди
служить для представлення знаку мантиси, а розряди 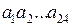 – модуля мантиси.
– модуля мантиси.
Двійкове число 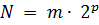 називається нормалізованим, якщо мантиса m задовольняє нерівності
називається нормалізованим, якщо мантиса m задовольняє нерівності
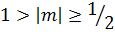 .
.
Тобто, двійкове число вважають нормалізованим, якщо в старшому розряді мантиси стоїть 1.
Оскільки для порядку|ладу| p (включаючи його знак) відведено сім розрядів, то порядок|лад| може бути цілим числом від -63 (1111111) до +63 (0111111).
Найбільше і найменше нормалізовані додатні числа в розрядній сітці відповідно рівні
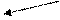 Правило нормалізації | m | ≥ ½
Правило нормалізації | m | ≥ ½
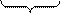
 і
і 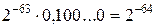 .
.
24 одиниці
Отже, з урахуванням|з урахуванням| знаку p у розрядній сітці можна представити|уявляти| числа, що лежать в діапазоні від  до
до  і від
і від  до
до  , що відповідає для абсолютних величин діапазону чисел приблизно від
, що відповідає для абсолютних величин діапазону чисел приблизно від  до
до 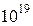 і значно перевищує діапазон чисел з|із| ФК, представлених у тому ж 32-розрядному слові.
і значно перевищує діапазон чисел з|із| ФК, представлених у тому ж 32-розрядному слові.
Число, що містить у всіх розрядах сітки 0, тобто має додатну нульову мантису і додатний нульовий порядок, називається дійсним нулем.
При фіксованій кількості розрядів мантиси будь-яка величина представляється в машині з|із| найбільшою можливою точністю нормалізованим числом. У процесі обчислен|підрахунків|ь може виходити ненормалізоване число. В цьому випадку машина |із|з ПК автоматично нормалізує його («нормалізація результату» операції).
Хай|нехай|, наприклад, ненормалізоване число  .
.
Після|потім| нормалізації воно набере вигляду  .
.
При виконанні деяких команд операція нормалізації блокується і отримуваний|одержувати| результат операції не піддається нормалізації.
У разі|у разі| нульової мантиси нормалізація неможлива.
В ЕОМ числа з|із| ПК представляються в шістнадцятковій системі числення відповідно до виразу|виразу| (рис. 4):
 , (1> m ≥1/16).
, (1> m ≥1/16).

Модуль порядку|ладу| p зображається цілим шестирозрядним двійковим числом, а мантиса m розглядається|розглядує| як число, складене з|із| шістнадцяткових цифр у вигляді|виді|:
 . (1.14)
. (1.14)
Використовуючи таку форму представлення і формат даних, отримуємо|одержуємо| діапазон для нормалізованих чисел:
від  до
до 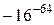
і від  до
до  ,
,
що відповідає для модулів чисел діапазону приблизно від 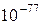 до
до  .
.
Як видно|показний|, така форма дозволяє набути значно більший діапазон чисел, ніж двійкова форма представлення|подання|.
У разі|у разі| шістнадцяткових чисел з|із| ПК число  вважається|лічить| нормалізованим, якщо старша шістнадцяткова цифра
вважається|лічить| нормалізованим, якщо старша шістнадцяткова цифра 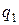 відмінна від нуля|нуль-елемента|. В нормалізованому числі три старші двійкові цифри можуть дорівнювати|рівнятися| 0. Це дещо зменшує точність представлення чисел при фіксованому числі розрядів мантиси.
відмінна від нуля|нуль-елемента|. В нормалізованому числі три старші двійкові цифри можуть дорівнювати|рівнятися| 0. Це дещо зменшує точність представлення чисел при фіксованому числі розрядів мантиси.
Зсув на один шістнадцятковий розряд виконується як зміщення мантиси відразу на 4 двійкових розряди, що дозволяє прискорити виконання деяких операцій.
Арифметичні дії над числами з|із| ПК вимагають виконання, окрім операцій над мантисами, певних операцій над порядками|ладами| (порівняння, віднімання та ін.). Для спрощення операцій над порядками|ладами| їх зводять до дій над цілими додатними числами, застосовуючи представлення чисел з|із| ПК із|із| «зміщеним порядком|ладом|».
У разі|у разі| представлення чисел із|із| зміщеним порядком|ладом| при записі числа в пам'ять до його порядку|ладу|  додається ціле число – зсув
додається ціле число – зсув  |зміщення|, де
|зміщення|, де  - число двійкових розрядів, використовуваних для модуля порядку|ладу|.
- число двійкових розрядів, використовуваних для модуля порядку|ладу|.
Зміщений порядок|лад|
 (1.15)
(1.15)
завжди додатний.
Для його представлення потрібна така ж кількість розрядів, як для модуля і знаку порядку|ладу| (рис. 5).
Важлива|поважна| особливість зміщених порядків|ладів| у тому, що, якщо для порядків|ладів|  і
і  , що є цілими числами із|із| знаками, має місце співвідношення:
, що є цілими числами із|із| знаками, має місце співвідношення:  , то і для додатних цілих величин відповідних зміщеним порядкам|ладам|
, то і для додатних цілих величин відповідних зміщеним порядкам|ладам|  і
і  завжди
завжди  .
.
Для формату числа з|із| ПК, показаного на рис. 5, зсув|зміщення|  . Для зберігання зміщеного порядку|ладу| виділимо сім розрядів з|із| номерами від 1 до 7, при цьому
. Для зберігання зміщеного порядку|ладу| виділимо сім розрядів з|із| номерами від 1 до 7, при цьому  може набувати значень від
може набувати значень від 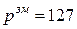 (при
(при  ) до
) до  (при
(при  ).
).

Використання чисел з ПК у форматі слова (рис.5) відповідає обчисленням приблизно з сімома десятковими розрядами, що для ряду науково-технічних розрахунків недостатньо через накопичення помилок округлення. Тому в ЕОМ для чисел з ПК передбачений також формат подвійної довжини, що займає два машинні слова (представлення з подвоєною точністю) (рис. 6).

У форматі подвійного слова не змінюється кількість розрядів для зображення порядку|ладу| і, отже, зберігається діапазон чисел, що представляються|уявляють|, а довжина мантиси збільшується до 14 шістнадцяткових розрядів. Використання такого подання еквівалентне виконанню обчислень|підрахунків| з|із| 15-16 десятковими розрядами.
Наявність у комп’ютерах декількох довжин форматів для представлення чисел дозволяє, враховуючи вимоги задачі|задачі|, обирати або короткі формати для чисел і, тим самим, економити об'єм|обсяг| пам'яті, зайнятої даними, і знижувати тривалість окремих операцій ЕОМ, або використовувати довгі формати для отримання більшої точності.
Окрім двійкових і шістнадцяткових, комп’ютер може зберігати і обробляти також десяткові числа і алфавітно-цифрові дані (тексти).
Максимальне додаткове число, що представляється|уявляє| при цьому, дорівнює  .
.
Найбільше від’ємне число, яке можна записати в доповняльному коді, визначимо таким чином. Вважатимемо|припускатимемо|, що найбільше від’ємне число  . Тоді зображення цього числа в доповняльному коді
. Тоді зображення цього числа в доповняльному коді  . Якщо до числа
. Якщо до числа  додати|добавляти| одиницю в самий молодший розряд, то в результаті отримаємо|одержуватимемо| число -1,00..0. Перетворивши це число по формальних правилах, отримаємо|одержуватимемо|
додати|добавляти| одиницю в самий молодший розряд, то в результаті отримаємо|одержуватимемо| число -1,00..0. Перетворивши це число по формальних правилах, отримаємо|одержуватимемо|  .
.
3. Похибки представлення чисел
Представлення числової інформації у цифровому автоматі, як правило, спричиняє за собою появу похибок (помилок), величина яких залежить від форми представлення чисел і від довжини розрядної сітки автомата.
Абсолютна похибка представлення – різниця між дійсним значенням вхідної величини 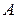 та її значенням, отриманим з машинного зображення
та її значенням, отриманим з машинного зображення 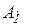 , тобто
, тобто  .
.
Відносна похибка представлення – величина
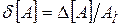 .
.
Вхідні величини, незалежно від кількості значущих цифр, можуть містити|утримувати| грубі похибки, що виникають через друкарські помилки, помилкові відліки показників яких-небудь приладів, некоректну постановку завдання|задачі| або відсутність повної|цілковитої| і точної інформації. Наприклад, часто приймають  . Проте|однак| ця величина може бути отримана|одержувати| з|із| вищою точністю (800 знаків і більше). Якщо прийняти, що точне значення
. Проте|однак| ця величина може бути отримана|одержувати| з|із| вищою точністю (800 знаків і більше). Якщо прийняти, що точне значення  , то абсолютна похибка дорівнює
, то абсолютна похибка дорівнює  .
.
Часто деяка величина в одній системі числення має кінцеве|скінченне| значення, а в іншій системі числення стає нескінченною величиною, наприклад, дріб  має кінцеве|скінченна| десяткове представлення|подання|, але|та|, будучи переведеним|переказувати| у двійкову систему числення, стає нескінченним дробом 0,0001100110011.
має кінцеве|скінченна| десяткове представлення|подання|, але|та|, будучи переведеним|переказувати| у двійкову систему числення, стає нескінченним дробом 0,0001100110011.
Отже, при переведенні|переказі| чисел з|із| однієї системи числення в іншу, неминуче виникають похибки, оцінити які неважко, якщо відомі дійсні значення вхідних чисел.
Числа зображаються в машині у вигляді  |виді|, де масштабний коефіцієнт
|виді|, де масштабний коефіцієнт  вибирають так, щоб абсолютне значення машинного зображення числа
вибирають так, щоб абсолютне значення машинного зображення числа  в системі числення з|із| основою
в системі числення з|із| основою  було завжди менше 1:
було завжди менше 1:
 .
.
Оскільки|тому що| довжина розрядної сітки ЕОМ дорівнює 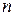 двійкових розрядів після|потім| коми, то абсолютна похибка переведення|переказу| десяткової інформації в систему з|із| основою
двійкових розрядів після|потім| коми, то абсолютна похибка переведення|переказу| десяткової інформації в систему з|із| основою  буде:
буде:
 . (1.16)
. (1.16)
Якщо  , то при
, то при  максимальне значення цієї похибки:
максимальне значення цієї похибки:
 . (1.17)
. (1.17)
З|із| останнього виразу виходить, що максимальна похибка переведення|переказу| десяткової інформації в двійкову не перевищуватиме одиниці молодшого розряду розрядної сітки автомата. Мінімальна похибка переведення|переказу| дорівнює нулю|нуль-елементу|.
Усереднена абсолютна похибка переведення|переказу| чисел у двійкову систему числення  .
.
Для представлення чисел у формі з|із| фіксованою комою абсолютне значення машинного зображення числа:
 .
.
Отже, відносні похибки представлення для мінімального значення числа
 .
.
Для ЕОМ, як правило  , тому 1>>2-n, звідки
, тому 1>>2-n, звідки  .
.
Аналогічно, для максимального значення:
 .
.
Звідси видно|показний|, що похибки представлення малих чисел у формі з|із| фіксованою комою можуть бути дуже значними.
Для представлення чисел у формі з|із| плаваючою комою абсолютне значення мантиси
 .
.
Похибка  - похибка мантиси. Для знаходження похибки представлення числа у формі з|із| плаваючою комою величину цієї похибки треба помножити на величину порядку|ладу| числа
- похибка мантиси. Для знаходження похибки представлення числа у формі з|із| плаваючою комою величину цієї похибки треба помножити на величину порядку|ладу| числа  :
:
 ;
;
 ,
,
де n – кількість розрядів для представлення мантиси числа.
З|із| цих виразів виходить, що відносна точність представлення чисел у формі з|із| плаваючою комою майже не залежить від величини числа.
Дата добавления: 2015-08-21; просмотров: 731 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Печать, тиражирование CD, DVD | | | ИСТОРИЯ ИСКУССТВ. ЗАПАДНОЕВРОПЕЙСКОЕ ИСКУССТВО |