Глава 10. Краевые задачи для обыкновенных дифференциальных уравнений.

1. Постановка задачи. Как уже говорилось, для получения решения дифференциального уравнения n-го порядка необходимо задать n дополнительных условий. Если условия задаются в одной точке, то они называются начальными условиями, а задача называется задачей Коши. Если же условия заданы в нескольких точках, то они называются краевыми условиями, а задача называется краевой. Очевидно, что краевую задачу можно поставить для уравнения как минимум второго порядка. Здесь мы будем рассматривать методы решения краевых задач именно для уравнений второго порядка, как для наиболее часто встречающихся.

Итак, имеется дифференциальное уравнение второго порядка

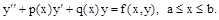
Отметим, что из f(x,y) часть, которую можно представить в виде q(x)y уже выделена и перенесена влево. На краях отрезка должны быть заданы краевые условия. Типичными вариантами их постановки являются следующие:

1. Заданы значения неизвестной функции. Например, краевое условие на левом краю имеет вид y(a)=c₁. Задача называется задачей первого рода или задачей Дирихле. Оба названия встречаются в литературе.

2. Заданы значения производной неизвестной функции. Например, краевое условие на левом краю имеет вид (a)=c₁. Задача называется задачей второго рода или задачей Неймана.

3. Заданы линейные комбинации значения и производной. Например, краевое условие на левом краю имеет вид . Задача называется задачей третьего рода.

Отметим, что на каждом краю может быть задано краевое условие своего рода. Их постановка зависит от физического смысла задачи.

2. Метод стрельбы. Как известно, полет снаряда выпущенного из пушки под углом к горизонту описывается системой двух дифференциальных уравнений второго порядка. При решении задачи Коши мы в качестве начальных условий задавали координаты точки выстрела х=0, y=0 и начальные компоненты скорости V_x0=V₀cos(a), V_y0=V₀sin(a), где a - угол наклона ствола. Подобный расчет может понадобиться например при испытаниях нового оружия, но при практических стрельбах, где стоит задача поразить цель, вряд ли окажется полезным. Здесь задачу надо ставить иначе - конечная точка полета снаряда соответствует координатам цели. Иначе - в задаче должны присутствовать условия x_n=L, y_n=H. Отметим, что n - требуемое количество шагов, нам здесь неизвестно. Но тогда условий в задаче становится шесть, а не четыре, т.е. имеем два лишних условия. Как правило убирают условия. задающие начальную скорость. В результате имеем краевую задачу.

Эмпирический метод ее решения давно используется в артиллерийской практике. Хорошо известно как это делается. Выстрел - получился перелет. Подправили прицел - получился недолет. Стреляем примерно со средним прицелом - цель поражена. Этот метод легко оформляется математически. Рассмотрим, как это делается.

Итак, мы умеем решать задачу Коши, т.е. задачу с начальными условиями, а нам нужно найти решение краевой задачи. В случае стрельбы по конкретной цели задачу, которую нужно решить, можно сформулировать так. Подобрать такой угол наклона орудия, чтобы снаряд упал на расстоянии L от точки выстрела. Возьмем произвольный угол наклона a, т.е. зададимся какими-то начальными условиями. Решим задачу Коши с этими условиями, т.е. найдем дальность полета. Скорее всего, в цель мы не попадем. Снаряд упадет на каком-то расстоянии L_x. Очевидно, что L_{x ­} зависит от a, т.е. мы можем сказать, что L_x=L(a), где L(a) - некоторая функция, значения которой вычисляются в результате решения задачи Коши, т.е. она задана не аналитически, а весьма неудобным способом. Но тогда всю задачу артиллериста можно сформулировать так - решить уравнение L(a)=L. Из формулировки выпало дифференциальное уравнение, но оно неявно присутствует в описании функции L(a). Решать ее можно любым доступным способом, например методами дихотомии или секущих. Например, при решении задачи дихотомией делаем несколько расчетов с наудачу выбранными параметрами a_i до тех пор, пока среди значений функции j(a_i)=L(a_i)-L не найдется двух разных по знаку. Очевидно, что необходимое значение a лежит где-то между этими точками. Объявляем эти точки начальными значениями концов отрезка и, деля этот отрезок пополам и производя “пристрелку” для каждого a, вычисляем необходимый угол с нужной точностью. Отметим, что действия артиллеристов, описанные выше, очень напоминают один шаг дихотомии.

Рассмотрим еще один вариант постановки задачи. Пусть решается уравнение

Заменой переменных сводим дифференциальное уравнение второго порядка к системе двух уравнений первого порядка. Получаем

У нас нет ни одного условия для второго уравнения, но зато два условия для первого уравнения. Очевидно, что использовать для решения подобной задачи методы типа Рунге‑Кутта невозможно. Согласно методу стрельбы для решения задачи в качестве недостающего начального условия задают произвольное значение z(a)=z_a и, считая получающееся решение y(b) функцией от z_a - y(b)=j(z_a), решают уравнение j(z_a)=y_b. Разница с предыдущим описанием заключается в том, что в задаче артиллериста нам неизвестна длина отрезка, т.е. время полета снаряда, и для окончания счета мы фактически использовали краевое условие - снаряд упал на землю, или координата y стала равна нулю.

Увеличение числа уравнений в исходной задаче ведет к тому, что нам придется решать не одно, а систему алгебраических уравнений, но смысл метода остается прежним.

Вообще говоря, в исходной постановке мы имеем краевую задачу, решить которую известными методами интегрирования обыкновенных дифференциальных уравнений мы не можем - не хватает начальных условий, но есть “лишние” условия в конечной точке счета. Задаваясь произвольными значениями недостающих условий, мы объявляем “лишние” условия функциями от недостающих сводим исходную задачу к решению одного или нескольких алгебраических уравнений. Тем самым, говоря на языке дифференциальных уравнений, мы заменяем решение исходной краевой задачи решением нескольких задач Коши.

Этот метод сведения решения краевых задач к решению последовательности задач Коши называется методом стрельбы (в англоязычной литературе - shooting). Особенно просто он реализуется в случае, если само уравнение и краевые условия линейны по искомым функциям и всем их производным. Пусть мы имеем краевую задачу

Для построения задачи Коши возьмем следующие начальные условия

Простой подстановкой можно убедиться, что эта пара условий удовлетворяет левому краевому условию. Совершенно очевидно, что теперь решение задачи Коши будет линейно зависеть от параметра h, поэтому функция j(h)=p₂u(b)+q₂v(b)-r₂ также будет линейной функцией от h. Но линейная функция, т.е. прямая, полностью определяется своими значениями в двух любых точках. Поэтому достаточно решить задачу Коши три раза - два первых позволяют определить искомое значение h, третий расчет дает требуемое решение задачи. Так как график прямой совпадает со своей секущей, до для расчета корня j(h) достаточно одного шага метода секущих. Отсюда имеем

.

Этот вариант метода называется линейной стрельбой (linear shooting).

3. Разностные методы. Метод конечных разностей является очень мощным и универсальным средством решения произвольных краевых задач. В данном разделе мы будем рассматривать только практические вопросы применения этого подхода. Прочие сведения будут изложены при изучении методов решения краевых задач для дифференциальных уравнений в частных производных. Отметим, что здесь мы будем рассматривать краевые задачи только для уравнений второго порядка, как наиболее часто встречающихся. При небольшом опыте все эти построения элементарно переносятся на уравнения более высоких порядков

При решении краевой задачи, как и при решении задачи Коши, решение исходного уравнения получается в виде таблицы значений функции. Но если в случае решения задачи Коши аргументы таблицы могут определяться в процессе расчетов, например в методах Рунге-Кутта с переменным шагом, то здесь аргументы таблицы задаются заранее. Для этого в области изменения независимых переменных вводится сетка, т.е. набор точек x₀=a < x₁ < x₂ <...< x_n < x_n+1=b. Точки x_i обычно называются узлами сетки, величины h_i=x_i-x_i-1 - шагами сетки.

Обозначим неизвестные значения искомой функции в узлах сетки как y_i=y(x_i). В исходном уравнении обязательно присутствует одна вторая производная (если ее нет, то краевую задачу поставить просто невозможно) и, может быть, первая производная. Запишем, аналогично тому, как это делалось при изучении численного дифференцирования, приближенные соотношения для этих производных, выражая их через y_i. Эти соотношения подставим в исходное дифференциальное уравнение вместо точных производных. Этот шаг называется построением разностной схемы, а его результат, т.е. уравнение, содержащее приближенные формулы для производных, - разностной схемой. Отметим, что теперь мы получаем некоторое алгебраическое соотношение, связывающее значения искомой функции в узлах заданной сетки.

Объединяя полученные соотношения во всех узлах сетки, мы получаем систему алгебраических уравнений. Но построить разностную схему мы можем только во внутренних узлах сетки. Поэтому полученная система содержит n уравнений, в то время как у нас имеется n+2 неизвестных. Для замыкания системы дополняем ее двумя соотношениями, следующими из краевых условий. Этот шаг называется учетом краевых условий.

Полученную замкнутую систему алгебраических уравнений решаем тем или иным известным нам способом. Результат - таблица значений функции, т.е. приближенное решение исходной дифференциальной задачи. Все четыре перечисленных шага - построение сетки, построение разностной схемы, учет краевых условий, решение алгебраической системы уравнений, обязательно присутствуют в любой программе, причем именно в указанном порядке. Иногда они оказываются тривиальными, иногда очень сложными.

Рассмотрим теперь все эти шаги на конкретном примере. Решается задача

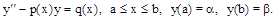
Шаг 1. Построение сетки.

Введем на отрезке [a,b] простейшую равномерную сетку, т.е. h_i=const=h. Нетрудно вычислить, что в этом случае h=(b-a)/(n+1), где n количество внутренних узлов. Координаты узлов можно найти как x_i=a+hi, i=0,...,n+1.

Шаг 2. Построение разностной схемы.

При изучении приемов численного дифференцирования была получена формула . Подставляя это выражение вместо второй производной в исходное уравнение в точке x_i, получаем

или, приводя подобные,

.

Теоретически построение разностной схемы окончено, но для написания программы этого мало. Рассмотрим вопрос, как мы в итоге собираемся решать готовую систему. Очевидно, что матрица системы уравнений имеет трехдиагональную структуру. Лучшим методом решения таких систем является прогонка. Как известно, i-е уравнение системы, решаемой прогонкой, имеет вид a_iy_i-1-b_iy_i+c_iy_i+1=d_i. Предполагая, что программа прогонки у нас есть, приведем нашу систему к виду, пригодному для решения этой программой. Для этого достаточно заполнить коэффициенты a,b,c,d - . Теперь построение разностной схемы завершено.

В заключение отметим следующий факт. Интерес к трехдиагональным системам вызван именно тем, что при решении разностными методами краевых задач для уравнений второго порядка возникают именно такие системы. Отметим, что теперь мы имеем положительный коэффициент b, для чего и был выбран знак минус в записи общего уравнения трехдиагональной системы.

Шаг 3. Учет краевых условий.

Уже говорилось, что мы получили систему из n уравнений с n+2 неизвестными. Вообще говоря, можно просто дополнить систему двумя элементарными уравнениями y₀=a, y_n+1=b в качестве первого и последнего уравнений системы.

Часто используется еще один вариант. Неизвестное y₀ присутствует только в первом уравнении a₁y₀-b₁y₁+c₁y₂=d₁. Подставим значение y₀=a в это уравнение. Получаем a₁a‑b₁y₁+c₁y₂=d₁. Но теперь первое слагаемое в левой части число, поэтому перенесем его направо: ‑b₁y₁+c₁y₂=d₁- a₁a. Так как в программах прогонки как правило не предусмотрены действия с коэффициентами, то их перед расчетом надо проделать отдельно, т.е. d₁:=d₁-a₁a; a₁:=0; Аналогичные действия производим на правом конце отрезка d_n:=d_n-c_nb; c_n:=0;

Для краевых условий второго рода отличие очень незначительно. Пусть условие на левом краю имеет вид . Записывая вместо производной разностное соотношение, получаем . Как и в случае условий первого рода подставим это соотношение в первое уравнение системы. Имеем a₁(y₁‑ah₁)‑b₁y₁+c₁y₂=d₁ или ‑(b₁‑a₁)y₁+c₁y₂=d₁+a₁ah₁. Теперь требуемое преобразование коэффициентов очевидно: b₁:=b₁‑a₁; d₁:=d₁+ a₁ah₁; a₁:=0;.

Случай, если производная задана на правом краю, ничем не отличается. Здесь имеем 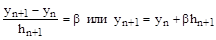, a_ny_n‑1‑(b_n‑c_n)y_n=d_n-c_nbh_n+1 откуда b_n:= b_n‑c_n; d_n:= d_n-c_nbh_n+1; с_n::=0;

Шаг 4. Решение системы.

Теперь, когда все уже готово, достаточно вызвать стандартную программу прогонки.

4. Некоторые сложности. Здесь была рассмотрена простейшая задача. Но при решении реальных задач могут возникать некоторые дополнительные, не рассмотренные здесь вопросы. Разберем некоторые из возможных усложнений по этапам, на которых они могут возникать.

4.1.Неравномерные сетки. Рассмотрим краевую задачу

.

Точное решение задачи y=exp(‑x), в чем нетрудно убедиться подстановкой. График решения приведен на рис.9.1. Как видно, функция достаточно быстро меняется на интервале от 0 до 2 и практически стабилизируется при х > 4. Решать такую задачу на равномерной сетке невыгодно, так как для хорошей передачи поведения решения около нуля сетка должна быть достаточно мелкой, в то время как при больших х шаги сетки можно выбирать большими. Иначе, если мы возьмем мелкую сетку, то проделаем много лишних вычислений при больших х, если же возьмем крупную, то резко потеряем в точности. Для разрешения этого противоречия при решении подобных задач, а они достаточно часто возникают в вычислительной практике, строят неравномерную сетку, т.е. сетку с переменным шагом. Как уже говорилось, при построении формул численного дифференцирования отличные результаты дают квазиравномерные сетки. Рассмотрим один из методов построения сетки с шагами, изменяющимися как геометрическая прогрессия, т.е. h_i+1=qh_i. Очевидно, что для построения такой сетки нам достаточно задать ее первый шаг h₁ и знаменатель прогрессии q, что можно сделать, построив два уравнения их объединяющих и решив полученную систему.

Первое требование, которому должна удовлетворять сетка - сумма шагов дает длину области. Очевидно, что сетка вида x₀=a<x₁<..< x_n<x_n+1=b, h_i=x_i-x_i-1 имеет n+1 шаг. Отсюда

h₁+...+h_n+1=h₁+qh₁+...+qⁿh₁=h₁(1+q+...+qⁿ)=b-a.

Учитывая формулу суммы геометрической прогрессии 1+q+...+qⁿ=(qⁿ⁺¹-1)/(q-1) имеем h₁(qⁿ⁺¹-1)/(q-1)=b-a. Это первое уравнение. Второе уравнение можно получить, задавая координату k-го узла сетки, что даст h₁(q^k-1)/(q-1)=x_k. Но простейшее решение получается, если n+1 четно и k=(n+1)/2. Тогда, разделив первое уравнение на второе, получаем q^k+1=(b‑a)/x_k. Отсюда элементарно находим q. Подставляя найденное q в любое из уравнений находим h_1. Теперь сетка построена. Изменяя значение x_k, мы можем эффективно управлять построением сетки, увеличивая или уменьшая ее сгущение у любого края. Остается напомнить формулы для аппроксимации производных на неравномерной сетке

Отметим некоторые полезные свойства этих формул, позволяющие сокращать объем программ и, тем самым, уменьшать возможности ошибок. Во-первых - в формуле для второй производной коэффициент при y_i равен сумме коэффициентов при y_i-1 и y_i+1, во-вторых - в формуле для первой производной коэффициенты при y_i-1 и y_i+1 отличаются только знаком. Эти свойства можно и нужно использовать в программах.

4.2. Краевые условия, заданные на бесконечности. Достаточно часто возникает задача, когда из физики процесса известно только асимптотическое поведение исследуемого параметра. Отсюда следует, что точное краевое условие известно нам только на бесконечности. Вообще говоря, можно выбрать достаточно большую область и решать задачу в ней, считая асимптотическое решение точным значением исследуемой величины на границе этой области. Прием может вести к хорошим результатам, но, к сожалению, без точного решения задачи слова “достаточно большая” остаются очень неопределенными. В итоге, если мы не угадаем требуемую величину области, наше решение может оказаться весьма далеким от истинного.

В этом случае хороших результатов можно добиться заменяя независимую переменную. Как известно, преобразование x=arctg(x) переводит интервал [0,¥) в интервал [0,p/2], а интервал (-¥,¥) в интервал [-p/2,p/2]. Тогда, если в качестве независимой переменной мы будем использовать не х, а x=arctg(x), то относительно x область расчета станет конечной. Но возникает дополнительное осложнение - в производных нам также нужно перейти к новой независимой переменной. Из формул дифференцирования сложных функций известно, что В то же время Отсюда имеем .

Для получения выражения для второй производной заметим, что

Последнее, что необходимо сделать - окончательно избавиться от х в дифференциальном уравнении. Для этого заметим, что В итоге все формулы перехода к новой независимой переменной выглядят следующим образом

Конкретный пример. Решается уравнение

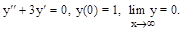
Из постановки задачи следует, что точное краевое условие у нас задано на бесконечности. Применяем описанную замену, т.е. подставляем вместо производных и функций от х их новые выражения. Получаем новую краевую задачу, заданную уже на конечном интервале -

В данном случае возможно еще и дополнительное упрощение. Сокращая все уравнение на cos²(x) получаем

Отметим, что при решении данной задачи необходимо очень сильное сгущение сетки на правом краю. Как сильно ее надо сгущать, можно определить только экспериментально, проводя расчеты с разными сетками и, сравнивая полученные результаты, добиваясь того, что дальнейшее сгущение сетки перестает влиять на решение. Естественно, что окончательные результаты расчетов необходимо выдавать в виде у(х), а не у(x), пересчитывая значения независимой переменной как x=arctg(x).

4.3. Построение разностных схем. В случае, если в уравнении есть только производные вида то вполне можно обойтись использованием приближений, полученных при изучении численного дифференцирования. Но в предыдущем разделе мы получили уравнение, содержащее слагаемое вида . Здесь вид разностной схемы уже не очевиден. Вообще говоря, можно записать это слагаемое в виде , но такой прием усложняет вид алгебраической системы, маскирует физический смысл слагаемых и, по этой причине, как правило не используется. Рассмотрим, как принято строить схему в этом случае.

Решается дифференциальное уравнение . Краевые условия нас в данный момент не интересуют. Для построения разностной схемы рассмотрим три подряд лежащих узла сетки. Проинтегрируем уравнение от точки х_i‑0.5 до точки х_i+0.5. Получаем

.

Первый интеграл в левой части можно взять точно, второй и третий найдем по формуле средних.. В результате имеем.

. Учитывая, что 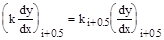и, заменяя производные известными разностными аппроксимациями, получаем итоговую разностную схему

которую, разделив все выражение на 0.5(h_i+h_i+1), легко привести к знакомому виду

Этот метод построения разностной схемы называется методом баланса.

4.4 Нелинейные задачи. Мы будем рассматривать уравнения, нелинейные только относительно искомой функции, а не ее производных.. Например, мы имеем уравнение . Разностную схему получаем используя разностные аппроксимации производных. Результат имеет вид

.

Но, к сожалению, прогонкой подобную систему решить нельзя - она нелинейна. Но именно такие задачи мы рассматривали, изучая линеаризацию по Ньютону. Отсюда вывод - полученную систему надо линеаризовать и затем решать итерационным методом, например - верхней релаксацией.

Дата добавления: 2015-08-21