Перегрузки в криволинейном полете

3.3.1. Общие выражения для определения перегрузок
при дви­жении самолета в вертикальной плоскости

Перегрузки при дви­жении самолета в вертикальной плоскости определим из соответству­ющих уравнений движения самолета. Эти уравнения в поточной си­стеме координат (см. рис. 3.1) могут быть записаны так:

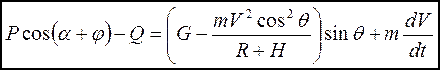
(3.5 a)

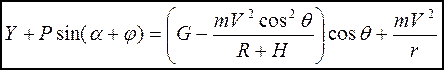
(3.5 б)

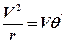где и - тангенциальное и нормальное ускорения соответ-ственно, м/с²;

r - радиус кривизны траектории, м;

Ө - местный угол наклона траектории, градусы;

V - скорость полета, м/с;

- центростремительное ускорение, обуслов­ленное кривизной поверхности Земли;

R y 6 370 000 м - радиус Земли;

Н - высота полета, м.

Центробежные силы инерции , обусловленные кривизной поверх-ности Земли, надо включать в уравнения (3.5) лишь при больших скоростях полета (М > 6 …7).

Разделив левые и правые части уравнений (3.5) на силу тяжес­ти G, получим формулы для определения тангенциальной и нор­мальной перегрузок, выраженных через поверхностные силы:

(3.6 а)

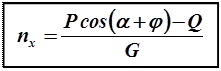
(3.6 б)

Аналогично через массовые силы:

(3.7 a)

(3.7 б)

Здесь - первая космическая скорость, которая равна 7,92 км / с;

g - ускорение силы тяжести.

При числе Маха М < 6…7 выражение и формула (3.7 б) принимает вид

(3.7 в)

Формулы (3.6) и (3.7) позволяют находить перегрузки п_х и п_у по известным силам, действующим на самолет, или по известным параметрам движения - V, r, 𝜽и𝜽 ^'

Определяя знаки перед чле­нами выражения (3.7 в), можно пользоваться следующими прави­лами:

Рис. 3.3 Определение знаков перед чле­нами выражения (3.7 в)

1. Если вектор силы тяжести самолета проектируется на от­рицательное направление оси у (рис. 3.3), то перед cos θ ставят знак "плюс", в противном слу­чае - "минус".

2. Второй член при­нимают сплюсом, если положи­тельное направление оси у обра­щено в сторону вогнутости тра­ектории, в противном случае перед ним надо ставить знак "минус".

3.3.2. Горизонтальный полет.

Вустановившемся горизонтальном полете , sinθ = 0, cosθ = 1 и из выражения (3.7) получим

.

Условие п_у = 1 обязательно для горизонтального полета. Продольная перегрузки п_х, может отличаться от нуля, но при этом полет протекает с ускорением.

3.3.3. Перегрузки при криволинейном полете в горизонтальной
плоскости.

В случае обычной схемы самолета криволинейный полет в горизонтальной плоскости (вираж) выполняется с креном (рис. 3.4).

сила y· sin g искривляет траекторию. Здесь
g - угол крена.

Если скольжение на крыло отсутствует, то боковая перегрузка n_z = 0. Поперечная перегрузка определяется из условия равновесия самолета

Y· cos у = G:

Рис. 3.4 Нагрузки при вираже

(3.8)

С увеличением угла крена перегрузка п_у возрастает. При g = 70° величина п_у близка к 3.

В полете со скольжением и при изменении высоты перегрузка может существенно отличаться от значения, получаемого по форму­ле (3.8).

Перегрузки п_у, которые обычно достигаются при маневрах

Маневр	пу
Вираж	3…5
Боевой разворот	3…6
Бочка	4…5
Петля Нестерова	5…6
Спираль	3…5
Полупетля с переворотом	4…5
Бочка многократная	5…7

\ 3.3.4. Полет вне границ атмосферы.

В этом случае аэродинамиче­ские силы y = 0, Q = 0 (рис. 3.5) и согласно выражению (3.6) пе­регрузки в направлении связан­ных осей координат равны

Если двигатель не работает (Р = 0), то
п_х = п_у = 0.

Из уравнения (3.5 б) следует, что при движении аппарата по круговой орбите с неработающим двигателем (Р = 0, Y = 0, cosθ = 1, 𝜃' = 0) вес его уравновешивается центробежными силами инерции, обусловленными кривизной поверхности Земли:

Это условие выполняется при скорости полета, равной первой космической
скорости V = V_k1

3.4. Перегрузки масс, не лежащих в центре тяжести
самолета

Если вращение самолета относительно центра тяжести отсутствует и он рассматривается как жесткое тело, то все его части испытывают одинаковые ускорения и одинаковые перегрузки, равные пере­грузкам п_Уо и п_хо в центре тяжести.

При вращении самолета с угловой скоростью ω и ускорением e линейные ускорения в различных его точках будут неодинаковыми. В i – ой точке самолета (рис. 3.6), расположенной на расстоянии х от центра тяжести (ц. т.), добавятся ускорения относительного дви­жения — нормальное D j_n= - ω² x и тангенциальное D j_τ = ex.

Этим ускорениям соответствуют перегрузки

и

Суммарные перегруз­ки i -ой массы при этом равны

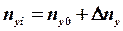(3.9)

В общем случае составляющие перегрузки i -ой массы, расположен­ной на оси самолета на удалении х от центра тяжести равно

; ;

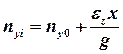где 𝛚 _y, 𝛚 _z - угловые скорости относительно осей у и z соответственно.

Их размерность с^-1;

- угловые ускорения относительно тех же осей, с^-2;

М_у, М_г, J_y, J_z - моменты поверхностных сил и мас­совые моменты инерции самолета относительно осей у и z соответственно. По длине самолета перегрузки изменяются линейно (см. рис. 3.6).

Пример. Приняв 𝝎 _z = 0,25 с ^-1 и расстояние массы от центра тяжести само­лета равным х = 5 м, найдем дополнительную перегрузку Dп_х в точке i:

Дополнительная перегрузка Dп_у обычно больше.

Например, полагая маневрен­ную нагрузку на оперении p _ман = 3000 кгс, плечо горизонтального оперения L_го= 5 м, момент инерции самолета
J_z = 5000 кгс×с²×м, найдем, что

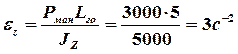и

---

Дата добавления: 2015-08-21