Случайные величины

1. Два орудия стреляют по цели; вероятности попадания в цель при одном выстреле для них равны соответственно 0,7 и 0,8. Для случайной величины Х (числа попаданий в мишень при одном залпе) составить ряд распределения, построить полигон распределения (график плотности распределения вероятности), математическое ожидание.

2. Случайная величина Х задана функцией распределения

Найти вероятности того, что в результате испытания Х примет значение: а) меньше 3; б) не меньше 3; в) из промежутка [0; 2, 6); г) из промежутка [3; 5).

3. Случайная величина Х задана плотностью распределения f (x) = ax² + 4,5x − 6 при x∈[2;4]; f (x) = 0 при x∉[2;4]. Найти параметр a, математическое ожидание.

4. Случайная величина Х задана функцией распределения

Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.

5. Случайная величина Х задана на всей числовой оси функцией распределения F(x)= 0,5+ 1/π*(arctg x). Найти вероятность того, что в результате испытания Х примет значение: а) заключенное в промежутке [0; 1); б) заключенное в промежутке [-1; 3).

6. Случайная величина Х задана функцией распределения:

Найти вероятность того, что в результате испытания Х примет значение: а) из промежутка [-1; 1); б) из промежутка [0; 5); в) из промежутка [-3; 1).

7. Задана плотность распределения непрерывной случайной величины:

Найти функцию распределения F(x).

8. Задана плотность распределения непрерывной случайной величины:

Найти функцию распределения F(x).

9. Плотность распределения непрерывной случайной величины Х задана формулой

Найти параметр С. Найти вероятность того, что Х примет значение из интервала (-1; 1).

10. Непрерывная случайная величина Х задана плотностью распределения

Найти вероятность того, что в трех независимых испытаниях случайная величина Х примет ровно два раза значение из интервала (0; π/4).

11. Дискретная случайная величина Х принимает три возможных значения: x₁ = 4 с вероятностью 0,5, x₂ = 6 с вероятностью 0,3 и x₃ с вероятностью p₃. Зная, что m_X = 8, найти x₃, p₃.

12. Найти моду и математическое ожидание дискретной случайной величины, заданной законом распределения:

13. Найти дисперсию и среднее квадратическое отклонение случайной величины Х, заданной рядом распределения:

а)

б)

в)

14. Непрерывная случайная величина Х задана плотностью распределения f (x) = a*x*cosx при x принадлежит [0;π/2]; f (x) = 0 при x 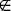[0;π / 2]. Найти параметр a и математическое ожидание.

15. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью распределения

f (x) = 0,04exp(−0,04x) при x ≥ 0; f (x) = 0 при x < 0.

Найти вероятность того, что в результате испытания Х попадет в интервал (1; 2).

16. Время исполнения заказа на ремонт радиоаппаратуры имеет показательный закон распределения со средним временем исполнения в 5 суток. Какова вероятность того, что сданный Вами в мастерскую магнитофон починят не ранее чем через 4 суток?

Ответ: 0,449

17. Длительность времени безотказной работы элемента имеет показательное распределение F(t) =1− exp(−0,01t), t > 0 − время в часах. Найти вероятность того, что за время длительностью 50 ч: а) элемент откажет; б) элемент не откажет.

Ответ:

18. Испытываются два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение F1(t) =1− exp(−0,02t), второго F2 (t) =1− exp(−0,05t), t − время в часах. Найти вероятность того, что за 6 часов: а) оба элемента откажут; б) оба элемента не откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.

Ответ:

19. Время ожидания в очереди имеет показательный закон распределения со средним временем ожидания 20 мин. Какова вероятность того, что покупатель потратит на покупку не менее 10 и не более 15 мин?

Ответ: 0,134

20. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервал (12, 14).

Ответ: 0,136

Дата добавления: 2015-08-21