Задача покрытия схем набором конструктивных модулей.

В результате решения задачи покрытия каждый элемент схемы привязывается к некоторому конструктивному модулю из набора Q={Q₁, Q₂, …,Q_m}.

Математическая постановка задачи покрытия зависит от типа конструктивных модулей набора. Различают 3 типа конструктивных модулей:

1) Каждый модуль содержит базовые логические элементы одного типа, при этом все входы и выходе логических элементов являются выводами модуля.

Например:

2) Тоже что и предыдущий тип, однако в одном конструктивном модуле могут содержаться разнотипные логические элементы.

Модули 1-го и 2-го типов называются модулями с несвязанными элементами.

3) Конструктивный модуль в общем случае содержит связанные между собой разнотипные элементы и не все входные и выходные выводы элементов имеются на внешних контактах конструктивного модуля.

Рассмотрим математическую постановку задачи покрытия схемы конструктивными модулями с несвязанными элементами (1-го и 2-го типов).

Обозначим через b_i количество логических элементов t_i типа, содержащихся в функционально-логической схеме (ФЛС). При таком подходе состав ФЛС может быть описан матрицей-столбцом: B= || b_i || _n, где n – число типов логических элементов схемы, b_i – число логических элементов t_i типа в ФЛС. Будем считать, что каждый тип конструктивного модуля Q_j в общем случае содержит несколько типов t_i базовых элементов, а весь набор конструктивных модулей Q может быть описан матрицей A= || a_ij || _nxm, где a_ij – количество базовых логических элементов типа t_i в конструктивном модуле типа Q_j ().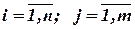

Пример.

			Q1	Q2	Q3
		t1
A	=	t2
		t3
		t4

В качестве критерия оптимизации будем использовать минимум стоимости покрытия. Обозначим c_j стоимость конструктивного модуля Q_j.

Пусть для покрытия ФЛС необходимо выделить y_j конструктивных модулей Q_j, тогда в качестве целевой функции можно взять функцию вида:

.

Будем считать, что каждый тип базового логического элемента схемы может быть реализован как базовый логический элемент того же набора, так и БЛЭ другого типа набора. Например:

Обозначим через x_ki количество логических элементов типа t_k, которое идет на покрытие логических элементов схемы типа t_i. Возможность замены БЛЭ типа t_k на БЛЭ типа t_i будем описывать матрицей W =|| w_ki || _nxn,

Очевидно, что x_ki >0 если w_ki =1.

Учитывая введенные обозначения, задачу покрытия можно сформулировать следующим образом: если y_j количество требуемых конструктивных модулей типа Q_j, а в каждом Q_j конструктивном модуле содержится a_ij элементов типа t_i, то определяет количество логических элементов типа t_i, содержащихся во всем выделенном для покрытия ФЛС наборе конструктивных модулей.

Очевидно, что для покрытия всей ФЛС необходимо выполнение следующего условия:

,

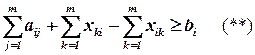где второе слагаемое – количество логических элементов других типов, которые идут в покрытии на реализацию логических элементов типа t_i; последнее слагаемое – количество логических элементов типа t_i, которые идут на реализацию логических элементов других типов.

Т. о., ставится задача отыскания таких значений y_j и x_ki, удовлетворяющих (**), чтобы обеспечивался минимум целевой функции (*) – стоимости покрытия. На практике используются приближенные методы, опирающиеся на специфику используемых конструктивных модулей. Если имеем дело с несвязанными элементами конструктивного модуля, то здесь в результате определения требуемого числа модулей не осуществляется привязка логических элементов схемы к конструктивным модулям, отсюда появляется возможность оптимизации по другому критерию, в частности по критерию минимума межблочных связей.

Пример Q={Q₁, Q₂, Q₃}, t={t₁, t₂, t₃, t₄} приведен нами выше. Требуется покрыть ФЛС, описываемую вектором B={ 5, 4, 1, 1 }, заданным набором конструктивных модулей.

Блок-схема алгоритма определения требуемого числа конструктивных модулей по критерию минимума стоимости покрытия приведена на рисунке.

Требуемое число корпусов модуля j-го типа определяется из выражения:

(1)

Для нашего примера:

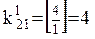
Так как a₃₁=0 и a₄₁=0, то в качестве коэффициента

Полагаем, что j=2 и вычисляем

, и следовательно

j=3

Переходим к :

, (остальные b_i=0)

Т.о. имеем , , , .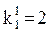

Эти данные подставляем в выражение (1) и определяем:

,

,

.

После определения требуемого числа корпусов, можно осуществить привязку элементов к корпусам. Для этого могут быть использованы рассмотренные ранее алгоритмы решения задач компоновки (задачи разбиения).

Дата добавления: 2015-08-21