Задача размещения конструктивных модулей

Различают два типа задач размещения:

1) размещение конструктивных элементов в заранее фиксированные позиции;

2) размещение элементов в непрерывном монтажном пространстве, когда позиции заранее не определены, а определяются в процессе размещения (например, проектирование БИС).

Рассмотрим первую задачу.

Пусть имеется регулярное монтажное пространство с уже фиксированными позициями 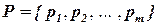, а также имеется количество элементов для размещения.

Будем считать, что длина связей определяется расстоянием между геометрическими центрами соответствующих позиций, т. е.

Чаще всего такая метрика используется тогда, когда последующая трассировка соединений осуществляется с помощью проводного монтажа «в навал» (провода с изоляцией). При использовании печатного или жгутового монтажа используются соответственно метрики (5.б) и (5.в):

где t – количество проводников в жгуте.

Метрики (5.б) и (5.в) обычно используют тогда, когда наряду с минимизацией суммарной взвешенной длины связей стараются минимизировать также длину наиболее длинной связи (она определяет время задержки схемы).

Если для простоты рассуждений положить m=n, то вариантов размещения будет n!, при этом любой вариант размещения может быть задан перестановкой 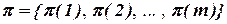, где π(i) – номер позиции, в которую устанавливается элемент e_i.

Сформулируем математическую постановку задачи размещения.

Пусть L(π) – суммарная длина межэлементных соединений, соответствующая некоторому варианту размещения π.

Пусть E_S – множество директивно размещенных элементов, к числу которых, в частности, относятся разъемы и внешние контактные площадки. Здесь S – множество индексов директивно размещенных элементов.

Рассмотрим некоторый произвольный заранее не размещенный элемент. Определим суммарную длину его связей со всеми директивными элементами. Обозначим эту длину как:

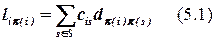
где c_is – элемент матрицы смежности ВНГ.

Суммарная взвешенная длина межсоединений недирективно размещенных элементов e_i и e_j определяется как:

С учетом (5.1) и (5.2) суммарная взвешенная длина межсоединений для варианта размещения π будет определяться из выражения (5.3):

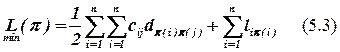
Таким образом, необходимо найти такой вариант размещения при котором обеспечивается минимум целевой функции (5.3). Это комбинаторная задача размещения.

Теперь рассмотрим постановку задачи целочисленного программирования.

Пусть перестановочная матрица (матрица решений) имеет вид:

На элементы матрицы решений X можно наложить следующие ограничения:

Т.е. каждому элементу соответствует одна позиция.

Каждый элемент может занимать только одну позицию.

При таком подходе суммарная взвешенная длина межсоединений может быть представлена следующим образом:

В выражении (5.7) первый член это суммарная взвешенная длина межсоединений между собой недирективно размещенных элементов, второй член – суммарная взвешенная длина межсоединений между недирективно размещенными и директивно размещенными элементами.

Необходимо найти такую булеву матрицу решений X, которая удовлетворяла бы ограничениям (5.4) и (5.6) и обеспечивала минимум целевой функции (5.7). Эта задача является квадратичной задачей целочисленного программирования.

В случае когда элементы не связаны между собой и заранее не фиксированы, а связаны лишь с директивно размещенными элементами, соответствующая задача является задачей линейного назначения. Этот факт используется в ряде приближенных алгоритмов размещения.

В настоящее время разработано много алгоритмов размещения, классификация которых приведена на рисунке 5.1.

Рис. 5.1. Классификация алгоритмов размещения.

Дата добавления: 2015-08-21