Нахождение величины F

Давайте сделаем таблицу, показывающую, какие по­казатели необходимы для вычисления F.

Показатель	Уровень звука
M X	M1	M2	M3	M4
∑ x ^2	∑ x 1^2	∑ x 2^2	∑ x 3^2	∑ x 4^2
n	n 1	n 2	n 3	n 4

Поскольку мы уже делали некоторые вычисления по четырем группам данных, давайте предположим, что они были получены и в эксперименте, где исследовалось влияние уровня громкости на время реакции. Назовем условие В уровнем 1, условие Г — уровнем 2, условие А — уровнем 3, условие Б — уровнем 4. Это избавит нас от большого числа вычислений. Кроме того, это даст нам уменьшение среднего времени реакции с уве­личением громкости — как и должно быть. Таким об­разом, главные показатели нами уже вычислены (см. гл. 6).

Показатель	Уровень звука
M X
∑ x ^2
n

Сумма квадратов для отдельной группы. Внутригрупповая (ВГ) сумма квадратов (СК) будет использована 3для определения оценки σ̅ ²х внутри группы. Она на­ходится простым сложением членов Σ²x по строке, поэтому

СК_ВГ = ∑ x₁² + ∑ x₂² + ∑ x₃² + ∑ x₄². (7.1)

Здесь

СК_ВГ = 4673 + 5391 + 5808 + 4306 = 20 178.

Сумма квадратов между группами. Межгрупповая сумма квадратов будет использована при определении оценки σ̅ ²х между группами. Для того, чтобы найти ее, вы сначала вычисляете общее («общ») среднее для че­тырех условий:

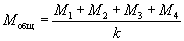, (7.2)

где k — число групп. Здесь

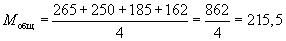
Затем ищется разность между каждым отдельным средним и общим средним. Такие разности обозначают­ся буквой d. Так,

d₁ = M_t — М _общ, d ₂= M ₂ — М _общ … (7.3)

Для числовых данных:

d ₁ = 265 — 215,5= +49,5; d ₂= 250 — 215,5 = +34,5;

d ₃ = 185 — 215,5= —30,5; d ₄= 162 —215,5 = —53,5.

Межгрупповая (МГ) сумма квадратов — это просто сумма квадратов величин d, умноженная на число случа­ев (n) по данному условию:

СК_МГ = n (d ₁² + d ₂²+ d ₃²+ d ₄² ). 7.4)

Для числовых данных:

СК_МГ = 17(2450,25 + 1190,25 + 930,25 + 2862,25) -= 17(7433) = 126361.

4 Внутригрупповое среднее квадратичное (СКВ_ВГ).

Оценка σ̅ ²х, основанная на внутригрупповой вариации, называется внутригрупповым средним квадратичным. Она находится делением суммы квадратов внутри групп на сумму степеней свободы для средних всех групп. Так, она равняется (n ₁—1) + (n ₂—1) + (n ₃—1),...

Поскольку мы имеем k условий и N испытуемых в целом,

df_ВГ = N — k. (7.5)

Для нашего эксперимента

df_ВГ = 68 — 4 = 64.

Как уже говорилось,

. (7.6)

Для наших данных

.

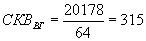Межгрупповое среднее квадратичное. Оценка σ̅ ²х, основанная на межгрупповой вариации, называется меж­групповым средним квадратичным (СКВ_МГ). Она на­ходится делением межгрупповой суммы квадратов начисло степеней свободы для общего среднего, вычислен­ного из средних для различных условий:

df_MГ = k — 1 ( 7.7)

А для числовых данных

df_MГ = 4 — 1 = 3.

Как уже говорилось,

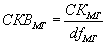. (7.8)

Или:

.

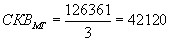5 F-отношение. Последний шаг в вычислении F-деление межгруппового среднего квадратичного на внутри-групповое среднее квадратичное. Вспомните, что чем больше это отношение, тем более вероятно, что нуль-ги­потеза может быть отвергнута:

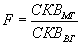. (7.9)

Или:

.

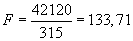Дата добавления: 2015-09-03