Модели стационарных временных рядов

Авторегрессионый процесс порядка может быть представлен в виде:

или

где

- оператор сдвига,

- оператор авторегрессии.

Для выполнения условия стационарности все корни многочлена должны лежать вне единичного круга, т.е. все корни соответствующего характеристического уравнения должны быть по модулю больше 1 и различны.

Простейший пример линейного авторегрессионного процесса – модель авторегрессии первого порядка - :

здесь - последовательность случайных величин, белый шум (пример стационарного ряда; в случае нормального распределения остатков – гауссовский белый шум).

Для белого шума:

является коэффициентом автокорреляции первого порядка и определяет значение коэффициента парной корреляции между соседними уровнями ряда:

Частная автокорреляционная функция (ЧАКФ) измеряет корреляцию между уровнями ряда при исключении влияния на эту взаимосвязь всех промежуточных уровней ряда, фиксируя их на среднем уровне:

Условие стационарности для определяется требованием .

На процесс с 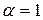внешне похож процесс случайного блуждания, т.к. каждое значение определяется случайным отклонением от предыдущего:

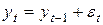
Случайное блуждание нестационарно, т.к. из 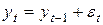с учётом некоррелированности и следует неравенство дисперсий и дисперсия может неограниченно возрастать со временем, т.е. влияние не затухает, а в стационарном процессе их влияние падает:

При процесс тем более нестационарный, т.к. подразумевает взрывные ряды, что маловероятно в экономических процессах.

Для AR(q) значения коэффициентов АКФ экспоненциально затухают (либо монотонно, либо попеременно меняя знак);

ЧАКФ имеют выбросы (пики) на первых q-лагах, остальные коэффициенты статистически незначимы.

Для проверки стационарности применяется тест Дики-Фуллера.

Тест рассматривает несколько вариантов модели:

1. отсутствие тренда: 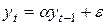(нулевое среднее)

2. положительная средняя: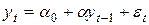

3. наличие временного тренда:

Преобразуем варианты моделей:

1.

2.

3.

Проверяем гипотезы:

будет отвергнута, если наблюдаемое значение критерия -статистики меньше значения, взятого из таблиц Дики-Фуллера. Значение критерия зависит от уровня значимости, размера выборки, вида модели.

Если нулевая гипотеза отвергается, то ряд относится к стационарным. Если нулевая гипотеза не отвергается, то возможно имеется единичный корень и исследуется модель случайного блуждания.

Модель скользящего среднего порядка q. MA(q) (c белым шумом)

Здесь каждое значение – среднее между текущей флуктуацией и несколькими предыдущими ошибками.

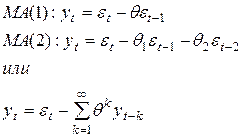
В последнем уравнении у, сгенерированный моделью МА(1) представлен в виде модели авторегрессии бесконечного порядка. Здесь , если оно больше 1, означает бесконечный (по мере удаления в прошлое) рост весов прошлых у, чего необходимо избегать.

Функция имеет выбросы (пики) на первых q лагах, а остальные значения статистически незначимы.

Значения АКФ для МA(q):

Например, для МА(1):

ЧАКФ задается выражением:

Это затухающая экспонента, где значения функции осциллируют с переменным знаком.

Для описания стационарных рядов может использоваться модель

авторегрессии – скользящего среднего (ARMA(p,q)

Здесь остаток – это скользящие средние из элементов белого шума.

Чтобы этот процесс был стационарным необходимо и достаточно, чтобы корни уравнения 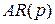-процесса лежали вне единичного круга, а все корни уравнения МА(p) -процесса вне единичного круга для обеспечения обратимости процесса.

Например, стационарность процесса ARMA(1,1) обеспечивается условием

, а обратимость .

Значения автокорреляционной функции для ARMA(1,1):

для

для , т.е.

значения АКФ будут экспоненциально убывать или монотонно (для , или знакопеременно (для .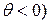

Модель ARIMA(p,q,d) или Бокса-Дженкинса применяется для нестационарных однородных рядов, т.е. рядов, в которых стационарным является остаток после вычитания из исходного ряда его неслучайной составляющей (f(t)).

Ряд должен включать аддитивную составляющую в виде алгебраического полинома, и после применения к нему процедуры последовательных разностей, может быть описан моделью (ARMA(p,q)). d- порядок разности

Методология ARIMA(p,q,d):

1. Обнаружение тренда (визуально)

2. Анализ АКФ и ЧАКФ для подтверждения стационарности: функции быстро убывают.

3. Тест на наличие единичного корня.

4. Рассчитывают последовательные разности (порядок разности определяется перебором вариантов)

5. После получения стационарного ряда (п.1-4) исследуется характер поведения АКФ и ЧАКФ и выдвигаются гипотезы о значениях параметров p(порядок авторегрессии) и q (порядок скользящего среднего). Формируется базовый набор функций.

6. МНК оцениваем параметры моделей.

7. Для проверки каждой пробной модели на адекватность анализируется ряд остатков. (Выборочные автокорелляции не должны отличаться от нуля).

8. Проверка значимости коэффициентов АКФ методом Бартлетта (каждых коэффициент автокорреляции отдельно) или методом Бокса-Пирса (множества коэффициентов как группы), а также методы Акайка и Шварца

9. Можно строить прогноз по выбранной модели.

Метод Бартлетта

Если модель адекватна, то распределение коэффициентов корреляции приближается к нормальному с дисперсией 1/n.

Поэтому, если коэффициент автокорреляции выходит за интервал

то нулевая гипотеза о равенстве нулю коэффициента отвергается.

Метод Q-статистика Бокса-Пирса

Q-статистика определяется:

При нулевой гипотезе об отсутствии автокорреляции статистика Q имеет

-распределение с степенями свободы.

Если , то первые 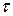коэффициентов автокорреляции значимы.

Информационный критерий Акайка

е – остатки.

Следует сделать выбор в пользу модели с наименьшим значением AIC.

Критерий Шварца.

Следует сделать выбор в пользу модели с наименьшим значением SIC.

Дата добавления: 2015-09-03