Фото 6. Некоторые природные фракталы: а) морская раковина; б) снежинка; в) капуста брокколи; г) хвост павлина

Фрактал – наиболее ёмкий показатель степени упорядоченности системы. Он связан с хаосом, как результат с процессом. Это геометрическая интерпретация детерминированного хаоса [309, 137, 161].

Фракталы позволяют отображать (а при необходимости и воспроизводить) окружающий нас мир строгим математическим языком, без обычно допускаемых для этого значительных упрощений [136, 215]. Овладев языком фракталов, можно описать форму облака так же чётко и просто, как архитектор языком традиционной геометрии описывает здание на чертежах.

С помощью фракталов стало понятно, каким образом, используя лишь небольшой набор простых элементов, создаются бесконечно сложно устроенные объекты (например, биологические).

Первыми открытымифракталами были так называемые детерминированные фракталы. Некоторые предпочитают называть их классическими, геометрическими или линейными фракталами [235].

В детерминированных фракталах самоподобие проявляется на всех уровнях. Это значит, что независимо от того, насколько вы приближаете фрактал, вы увидите все тот же узор.

Простейшими детерминированными фракталами являются снежинки Коха и ковер Серпинского (рис.21-а, -б). Все они обладают регулярной геометрически правильной структурой. Каждый фрагмент такого фрактала в точности повторяет всю конструкцию в целом.

Большая часть встречающихся в природе фракталов не являются детерминированными. Сложные фракталы не собраны из повторяющихся геометрических форм. Они генерируются нелинейными алгебраическими уравнениями. В качестве примера можно привес-
ти фрактал Жулиа или множество Мандельброта (рис. 21 -в, -г).

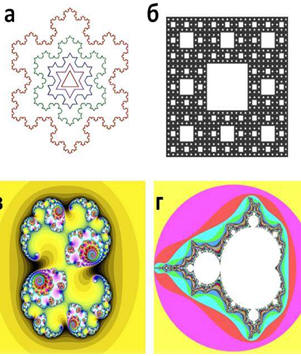
Рис. 21. Примеры простых и сложных фракталов: а) снежинка Коха; б) ковёр Серпинского; в) фрактал Жу-лиа; г) множество Мандельброта

В настоящее время фракталы и мультифракталы стремительно вторгаются во многие области биологии, медицины, социологии, экономики, метеорологии, физики полимеров, геоморфологии, теорий турбулентности и броуновского движения и т.п. [166].

Методы обработки изображений и распознавания образов, использующие новые понятия, дают возможность исследователям применить этот математический аппарат для количественного описания огромного количества природных объектов и структур.

Учение о фрактальной геометрии, согласно которому «все содержится во всем», соответствует принципам голографии и взглядам Дэвида Бома. Аттракторы, характеризующие детерминированный хаос – тоже фракталы.

Фрактальные структуры широко представлены в организме человека. Форму фрактала имеют легкие, мозг, кровеносная система и т.д.

Фракталы найдены и на субклеточном уровне организации живой системы – поверхность ядерной мембраны, цитоскелет. Было установлено, что значения фрактальной размерности ядерных мембран нормальных клеток по величине больше, чем у злокачественных клеток, причем эта разница относиться к самым ранним симптомам злокачественного перерождения клетки.

С точки зрения фракталов становится более понятным принцип соматотопического представительства органов и всего организма на ушной раковине, подошве стопы, слизистой оболочке рта и т.д. [246]

Справедливости ради следует заметить, что абсолютизация фракталов как универсальной модели для описания всех явлений природы, может быть оправдана лишь только в смысле «неимения лучшего». Мы пока не знаем всего разнообразия фракталов и не можем с уверенностью утверждать, является ли данный объект фрактальным или нет. Остаётся неясным, как далеко простираются модели подобного типа [246].

Солитоны. Известно, что в достаточном по глубине и ширине водоёме волны распространяются во все стороны от источника возмущения. Скорость их распространения прямо пропорциональна длине. Зародившись одновременно, такие волны постепенно рассеиваются по пути следования, подобно группе бегунов на длинные дистанции. В лидерах оказываются колебания большей длины, а в аутсайдерах – короткие. Таким образом, плотность волн будет падать с увеличением расстояния от источника генерации, что в конечном итоге приведёт к постепенному затуханию возмущения (рис. 22).

Рис. 22. Распространение линейных волн на поверхности воды

Всё сказанное относится к процессам относительно небольшой амплитуды и длины волны. Они описываются простыми линейными уравнениями (например, синусоидальными) и обладают такими хорошо известными свойствами, как интерференция, дифракция, дисперсия, рассеяние, отражение и преломление. Эти явления во многих случаях свойственны колебаниям звукового, светового и радиоволнового диапазона, а также наблюдаются в квантовой механике.

Если ограничить распространение волны по ширине и глубине, например, заставить её двигаться вдоль узкого неглубокого канала, то, отталкиваясь от дна и стенок водоёма, она будет иметь большую высоту и распространяться на гораздо большее расстояние.

Представим себе, что экстренно открылись створы плотины, и высокий вал воды устремляется из водохранилища в сравнительно узкое русло реки. При этом верхние слои потока, испытывая меньшее сопротивление, будут двигаться быстрее нижних, что придаст фронту волны загнутую вперёд пилообразную форму. Дальнейшее нарастание крутизны фронта приводит к «опрокидыванию» волны. Так рождаются нелинейные волны, их поведение описывается более сложными нелинейными уравнениями (рис. 23).

Рис. 23. Эволюция линейной волны в нелинейную: а) волна с синусоидальным (линей-ным) фронтом; б) укручение волнового фронта; в) опрокидывание волны

В отличие от линейных систем они почти не рассеиваются, распространяясь с большой скоростью на значительные расстояния. Ярким примером таких волн является цунами, а также распространяющиеся со сверхзвуковой скоростью раскаты грома, звуки выстрела, хлопанье кнута. Одним из признаков нелинейности колебаний, распространяющихся в жидкости, является появление «барашков» на их гребнях [156] (фото 7).

Впервые на подобное явление обратил внимание английский изобретатель Скотт Рассел в 1834 году, занимавшийся изучением судоходности барж на многочисленных каналах в окрестностях Эдинбурга.

Вот как он описал своё наблюдение: «Я следил за движением баржи, которую быстро тащила вдоль узкого канала пара лошадей. Когда внезапно баржа остановилась – вся масса воды в канале пришла в движение. Она собралась у носа корабля в состоянии бурного волнения, а затем вдруг оторвалась от него и покатилась с большой скоростью, приняв вид большого уединенного возвышения. Округлый, гладкий, четко выраженный холм воды продолжал свое движение по каналу без видимого изменения формы или уменьшения скорости. Я бросился за этой волной верхом на лошади и догнал ее, когда она все еще двигалась со скоростью около восьми миль в час, сохраняя первоначальную форму, и имела около тридцати футов в длину и до полутора футов в высоту. Ее высота постепенно уменьшалась, и после одной или двух миль погони я потерял ее в изгибах канала».

Рассел был уверен, что сделанное им открытие играет важную роль во многих явлениях в природе. Путём многочисленных экспериментов в длинном узком бассейне учёный установил, что в обнаруженных им уединённых волнах энергия, передаваемая жидкости, не рассеивается, не «размазывается» по всей поверхности, а устойчиво распространяется на значительные расстояния.

Окончательную ясность в проблему внесли голландские ученые – Дидерик Иоханнес Кортевег и его ученик Густав де Фриз в 1895 году. Волны, описываемые уравнением Кортевега – де Фриза, имеют несинусоидальную форму и становятся синусоидальными только в том случае, когда их амплитуда очень мала. При увеличении длины волны они приобретают вид далеко разнесенных друг от друга горбов, а при очень большой длине волны остается один горбик, который и соответствует «уединённой» волне (рис. 23-в, фото 7) [241].

Дата добавления: 2015-09-03