Рух в неінерційній системі відліку.

Нехай існують дві довільні системи відліку К- нерухома та К'- рухома. Співвідношення між радіус-векторами точки деякої точки А в нерухомій системі , в рухомій системі 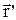та радіус-вектором початку відліку системи К' відносно системи К запишуться у вигляді

. (1)

Абсолютна швидкість – швидкість точки А в нерухомій системі відліку за визначенням є

. (2)

Радіус-вектор 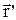має орт напрямку 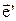і його можна записати так

.

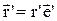Вектор 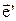обертається з кутовою швидкістю обертання рухомої системи відліку , а похідна від одиничного вектора (див.1.6 (2')) 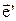по часу дорінює

.

Похідна від 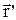по часові запишеться так

, (3)

де 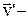швидкість точки А відносно рухомої системи координат і вона називається відносною швидкістю, a 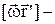лінійна швидкість точки.

Тепер абсолютну швидкість точки А можна записати так

, (4)

де

абсолютна швидкість поступального руху рухомої системи координат.

, (5)

де

, (6)

а

(7)

є кутове прискорення системи відліку К'.

Підставляючи (6-7) в (5) одержимо

(8)

Звівши подібні доданки у (8), маємо вираз для прискорення точки А

(9)

Розглянемо докладніше величину та напрямок вектора . Вектори 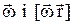взаємно перпендикулярні і тому можна записати

,

де 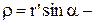відстань від точки А до осі обертання системи відліку К', а напрямок вектора протилежний напрямкові (див.Мал.11), тому можна записати

. (10)

Вектор в (10) є доцентовим прискоренням точки А. Підставляючи (10) в (9) одержимо остаточний вираз для абсолютного прискорення точки А через прискорення в рухомій системі відліку

. (11)

У виразі (11) складова прискорення називається коріолісовим або поворотним прискоренням точки А, зумовленим обертанням системи відліку К'.

Розглянемо окремі випадки руху системи відліку К'.

1. Система К' рухається поступально до системи К, тобто .

, (12)

2.Система К' обертається із сталою кутовою швидкістю навколо осі К з початком відліку О, що лежить на ній.

, (13)

3. Система К¢ обертається з навколо осі, що переміщується поступально з швидкістю 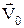та прискоренням по відношенню до системи К. Цей випадок об¢єднує два попередніх і являє собою додавання обох незалежних рухів, яке дає такий результат

. (14)

1.7. Контрольні питання

1. Що вивчає механіка?

2. Який фізичний зміст вкладається у поняття простору і часу?

3. Дайте визначення механічної системи, механічного руху, точки (системи) відліку.

4. Поясніть фізичні моделі матеріальної точки та абсолютно твердого тіла.

5. Що вивчає кінематика?

6. Дайте визначення вектора та наведіть правила додавання, віднімання, скалярного та векторного добутку векторів.

7. Дайте визначення та поясніть властивості

· радіус-вектора ,

· траєкторії,

· шляху S,

· переміщення ,

· радіуса кривизни та кривизни траєкторії, як їх знайти.

8. Дайте визначення похідної та диференціала функції.

У які величини переходять малі величини при спрямуванні .

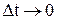9. Для чого вводяться системи координат та наведіть приклади таких систем.

10. Дайте визначення ступенів свободи механічної системи та узагальнених координат.

11. Як записуються в декартовій системі координат

· радіус-вектор положення тіла ,

· вектор переміщення ,

та як визначаються їх величини та напрямки?

12. Сформулюйте основну (пряму) задачу кінематики та алгоритм її розв'язку.

13. Наведіть приклади кінематичних рівнянь руху.

14. Дайте визначення дотичної до траєкторії.

15. Визначить тангенціальний та вектор нормалі до траєкторії.

16. Знайдіть похідну від одиничного тангенціального вектора .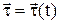

17. Дайте визначення середньої та миттєвої швидкості.

18. Знайдіть вектор і модуль середньої та миттєвої швидкості в декартовій системі координат.

19. Запишіть переміщення через швидкість.

20. Дайте визначення середнього та миттєвого прискорення.

21. Дайте визначення нормального та тангенціального прискорення.

22. Виведіть вирази для нормального та тангенціального прискорення.

23. Сформулюйте обернену задачу кінематики та алгоритм її розв'язку.

24. Знайдіть миттєву та середню швидкість і переміщення для рівноприскореного прямолінійного руху.

25. Дайте визначення обертового руху та його кінематичних характеристик

· кута повороту j,

· вектора малого кута повороту ,

· кутової швидкості,

· кутового прискорення,

та правило знаходження їх величин та напрямків.

26. Визначте період та частоту рівномірного руху матеріальної точки по колу.

27. Дайте визначення лінійних характеристик обертового руху та знайдіть їхній зв'язок з кутовими характеристиками.

Дата добавления: 2015-10-31