
|
Читайте также: |
1. ЦЕЛИ И ЗАДАЧИ ЛАБОРАТОРНОЙ ПРАКТИКИ
В УЧЕБНОМ ПРОЦЕССЕ КУРСА ФИЗИКИ
Лабораторный практикум, как составная часть учебного процесса по курсу физики, обеспечивает прочную связь познавательной и профессиональной направленности физических знаний. Относительная доля времени, отводимого на этот вид учебных занятий, в техническом вузе всё время возрастает.
Целью лабораторной практики студентов в вузе является:
1.Приобретение навыков в проведении эксперимента и ознакомление с методами обработки экспериментальных данных.
2. Ознакомление с различными приборами и приёмами прямых и косвенных измерений физических величин.
3.Наглядное подтверждение теоретических положений, излагаемых в лекционном курсе, в сильной степени помогающее понять и усвоить сущность различных физических явлений.
2. ОРГАНИЗАЦИЯ РАБОТЫ СТУДЕНТОВ В ФИЗИЧЕСКОЙ ЛАБОРАТОРИИ
Работа студентов в физических лабораториях проводится в соответствии с расписанием занятий, составляемым на семестр. В зависимости от числа часов, запланированных для экспериментальных работ (17...18 или 34...36 часов), занятия в лаборатории проводятся один раз в две недели или еженедельно. Продолжительность каждого занятия составляет два академических часа.
В течение семестра студенты выполняют установленное графиком количество лабораторных работ, объединённых в тематические циклы (кинематика и динамика поступательного и вращательного движений, электростатика, постоянный ток, молекулярная физика, колебания и волны и т.п.) по 2...4 работы в цикле. Каждый цикл работ завершается их защитой - собеседованием с преподавателем по
теории, методике и практике выполнения лабораторной работы После защиты выполненного цикла работ студенты допускаются к выполнению следующего цикла. Защита всех циклов лабораторных работ является основанием для допуска студента к зачёту по практическим работам и затем к экзамену. Лабораторная работа выполняется студентами в составе бригады из двух человек. При этом каждый из работающих ведёт свой протокол, в котором фиксируются результаты совместных измерений и обработки полученных результатов. Перед окончанием занятия результаты измерений предъявляются преподавателю, ведущему занятия в группе. Последовательность выполнения лабораторных работ каждой бригадой определяется графиком, составляемым на семестр и имеющимся в лаборатории. Каждому студенту следует его записать, чтобы получить в библиотеке соответствующий набор "Методических указаний для выполнения лабораторных работ по дисциплине "Физика" на кафедре "Физика-1". Методические указания необходимы для самостоятельной домашней подготовки к лабораторным занятиям. Результатом этой подготовки является конспект (протокол), включающий название лабораторной работы и её номер, краткое содержание теории работы, основные формулы, схема лабораторной установки с обозначениями измеряемых физических величин, расчётные формулы, заготовки таблиц, в которые заносятся результаты измерений в лаборатории и расчётов, примеры расчётов, содержащие обозначение рассчитываемой величины, используемой для этого расчёта формулы, формулы расчёта относительной ошибки измерения исследуемой величины. Если одна и та же величина в данной работе определяется несколькими разными способами, то пример расчёта приводится один раз для каждого способа. Во многих работах по результатам измерений и расчётов необходимо строить графические зависимости - поэтому необходимо отвести место в конспекте для построения графиков. Наиболее корректно это осуществляется построением графика на миллиметровой бумаге с соблюдением пропорций конспекта и масштабов, соответствующих полученным результатам. Затем этот график вклеивается в предусмотренное в конспекте место. По согласованию с преподавателем
допускается построение графиков непосредственно в конспекте в отведённом месте с применением чертёжных инструментов и с соблюдением всех правил оформления графиков. Работа над конспектом заканчивается оценкой погрешностей измерений и записью окончательного результата. Оформленный в соответствии с описанными правилами конспект представляет уже отчёт о выполненной лабораторной работе, сдаваемый преподавателю после собеседования (защиты) по циклу.
3. ОСНОВЫ ТЕОРИИ И ПРАКТИКИ
ФИЗИЧЕСКИХ ИЗМЕРЕНИЙ
Выполнение физических экспериментов, как правило, состоит в измерении физических величин. Измерить физическую величину - это значит сравнить её с какой-то другой однородной, принятой за единицу. Например, измеряя длину любого предмета, мы сравниваем его линейный размер с эталоном - метром. Первоначально за метр принимали одну сорокамиллионную долю парижского меридиана. В настоящее время принято другое определение метра: "Метр - длина, равная 1650763,73 длины волн излучения в вакууме, соответствующая переходу между уровнями 2 р 10 и 5 d 5 атома криптона-86". Массу мы сравниваем с эталоном, названным килограммом и т.д.
Различают прямые и косвенные измерения. В результате прямых измерений получаем непосредственно численное значение определяемой величины. Примером прямых измерений может служить измерение массы тела при взвешивании на рычажных весах, измерение расстояний с помощью мерной ленты и т.д. При косвенных измерениях значение интересующей нас величины получается путём расчёта по формуле, связывающей значение искомой величины с результатами прямых предварительных измерений. В косвенных измерениях, таких как определение объёма, сначала проводятся прямые измерения длины, ширины, высоты, углов, а затем при подстановке полученных значений в соответствующую формулу на-
ходим объём. В ряде случаев значение какой-либо величины может быть получено как с помощью прямых, так и с помощью косвенных измерений. Например, величину сопротивления проводника можно определить прибором - омметром, а так же вычислить по измеренной величине тока, протекающего по сопротивлению, и по величине падения напряжения на этом сопротивлении. Выбор способа измерений в каждом конкретном случае должен решаться с учётом удобства и скорости получения результатов, конечной точности, надёжности полученного результата, наличия соответствующей аппаратуры.
4. ОШИБКИ ИЗМЕРЕНИЙ ФИЗИЧЕСКИХ ВЕЛИЧИН
Результаты любых измерений а, следовательно, и вычисления, использующие эти данные, содержат те или иные ошибки.
Пусть истинное значение определяемой величины составляет " а ". Предположим, что в результате проведённых нами прямых или косвенных измерений для определяемой нами величины получено значение " x ". Тогда разность
D = | а - х | (1)
принято называть абсолютной ошибкой измерения. Размерность абсолютной ошибки совпадает с размерностью определяемой величины.
Для характеристики "качества" проведённых измерений принято вводить отношение абсолютной ошибки к значению измеряемой величины:

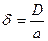 (2)
(2)
Это отношение называется относительной ошибкой измерения. На практике величина " а " неизвестна. В теории вероятностей показано, что наилучшим приближением к ней по результатам измерений служит среднеарифметическое:
 (3)
(3)
Поэтому для абсолютной и относительной ошибок измерений пользуются формулами:
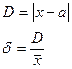 (4)
(4)
По происхождению все ошибки измерений можно условно разделить на методические, инструментальные и случайные ошибки измерений.
Методические ошибки определяются недостатками выбранного метода измерений, неточностью расчётной формулы. Примером первых ошибок могут служить ошибки, возникающие при измерении сопротивлений с помощью мостика Уинстона. Проходящий через измеряемое и эталонное сопротивления электрический ток нагревает их, по разному изменяя величины их сопротивлений, так как материалы, из которых изготовлены эти сопротивления, в общем случае, разные. Для уменьшения ошибок измерений в данной работе рекомендуется сокращать время протекания тока в измерительной цепи, уменьшать величину ЭДС источника.
Примером ошибок, возникающих из-за неточности расчётной формулы, могут служить ошибки при проверке основного закона динамики вращательного движения на маховике Обербека. Для расчёта момента сил, действующего на маховик (крестовину), используется формула: 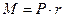 , где М – момент сил, Р – вес груза, подвешенного на нити и r – радиус шкива. На самом деле, вместо силы тяжести груза Р следует в расчетную формулу подставлять силу натяжения нити Т, отличающейся от веса Р на величину m*a, где m -масса груза и а - ускорение груза при движении вниз. Отличие это невелико, так как ускорение груза а обычно мало по сравнению с ускорением свободного падения g, и методические ошибки, возникающие при замене силы Т на силу тяжести Р, оказываются меньше, чем ошибки из-за пренебрежения силами трения, которые можно отнести к инструментальным погрешностям.
, где М – момент сил, Р – вес груза, подвешенного на нити и r – радиус шкива. На самом деле, вместо силы тяжести груза Р следует в расчетную формулу подставлять силу натяжения нити Т, отличающейся от веса Р на величину m*a, где m -масса груза и а - ускорение груза при движении вниз. Отличие это невелико, так как ускорение груза а обычно мало по сравнению с ускорением свободного падения g, и методические ошибки, возникающие при замене силы Т на силу тяжести Р, оказываются меньше, чем ошибки из-за пренебрежения силами трения, которые можно отнести к инструментальным погрешностям.
Инструментальные ошибки определяются недостатками используемого прибора, качеством его изготовления, неправильным его применением и проявляются в том, что при измерениях одним и тем же прибором получают повторяющиеся результаты. Такая ситуация означает, что в данных измерениях, если они проводятся методически правильно, преобладающими являются инструментальные ошибки. В качестве примера инструментальной или, что то-же самое, приборной ошибки можно привести ошибки, возникающие при употреблении для измерений приборов, использующих различные нониусы (штангенциркули, микрометры, угломеры и т.д.). Для таких приборов в качестве приборной ошибки принимают цену деления нониуса. То же самое применимо при отсчёте интервалов времени с помощью секундомера. В этом случае приборная ошибка принимается равной цене наименьшего деления.
В электроизмерительных приборах (вольтметрах, амперметрах и т.п.) инструментальная ошибка определяется классом прибора "К", который означает, что показания прибора в любой точке шкалы отличаются от истинного значения измеряемой величины не более, чем на "К" процентов от всей шкалы прибора. Так, например, при использовании вольтметра класса 0,5 со шкалой до 300 В отличие показаний прибора от истинного значения любого измеряемого напряжения не превышает (0,5/100)·300 В = 1,5 В в любой точке шкалы. О знаке этой ошибки ничего сказать нельзя.
На результат измерений может влиять целый ряд факторов. Так, например, изменение положения глаз измеряющего при повторных измерениях может привести к ошибкам из-за параллакса при отсчёте результата. При использовании многопредельных приборов считывание показаний не по рабочей шкале приводит к грубым ошибкам, классифицируемым как промахи, которые хорошо заметны при анализе всей совокупности результатов измерений. Такие измерения обычно отбрасываются.
Следует упомянуть так же об ошибках, которые могут быть либо постоянными в процессе измерений, либо меняться по определённому закону. Так, например, использование прибора со смещённым "нулём" приводит к появлению постоянной систематической ошибки. При взвешивании тел на рычажных весах истинный вес тела может отличаться от полученного при измерениях вследствие неравенства плеч коромысла, за счёт поправки на выталкивающую силу в воздухе, из-за изменения температуры в процессе измерений. В данном случае первая ошибка будет постоянна, вторая и третья будут меняться по определённому закону, так как выталкивающая сила зависит от объёма тела и гирь, влажности воздуха, изменений объёмов и т.д. Во многих случаях величину и знак систематической ошибки можно установить с помощью наблюдений или измерений. Такие выявленные ошибки называют поправками. Поправки принято считать равными ошибке измерений, взятой с обратным знаком.
Систематические ошибки, связанные с неправильной градуировкой, с "уходом нуля" и т.п. могут быть выявлены при сравнении с эталонным прибором или измерением эталонной величины Систематические ошибки, связанные с неточностью метода, выявляются при анализе расчётных формул, рассмотрении пределов их применимости, анализе допущений, сделанных при выводе расчётных выражений. Возможности уменьшения систематических ошибок существенно зависят от объёма информации о природе этих ошибок и от усилий, которые необходимо затратить на их исключение. В простейшем случае, когда природа и величина ошибки известны, для их исключения пользуются поправками. Если происхождение систематической ошибки не установлено, а известно лишь максимальное значение, которое она может принимать, то говорят, что существует не исключаемый остаток систематической ошибки. Но самым опасным видом систематической ошибки может быть такой, о котором экспериментатор и не подозревает. Чтобы убедиться, что такой ошибки нет, проводят измерение каким-либо другим методом, совершенно отличным от используемого. Совпадение результатов убеждает, что неучтённых систематических ошибок нет.
Если при многократных измерениях одной и той же физической величины её значения, с учётом методических, систематических и приборных ошибок оказываются разными, но мало отличающимися от среднеарифметического всех полученных значений, то говорят о случайных ошибках измерений. Эти ошибки, как правило, бывают больше инструментальных и могут иметь как положительный, так и отрицательный знаки. Улучшая условия измерений, случайные ошибки удаётся лишь уменьшить, но устранить их полностью нельзя. Учёт этих ошибок осуществляется путём статистической обработки результатов измерений, которые при многократных повторениях подчиняются следующим закономерностям:
1. Средние значения измеряемой величины при достаточно большом числе измерений, проведённых одинаково тщательно, остаются практически постоянными;
2. Частота появлений как положительных, так и отрицательных отклонений от найденного среднего значения примерно одинакова.
3. Частота больших отклонений от найденного среднего значения значительно меньше частоты появления малых отклонений.
Математическая статистика даёт формулы для расчёта вероятности появления того или иного результата "х" при измерениях некоторой физической величины с истинным значением "а":
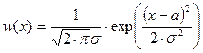 (5)
(5)
где w (x) - функция распределения случайных величин, связанная с вероятностью получения значения " х " при измерении величины, истинное значение которой равно " а "; " е " - основание натуральных логарифмов, равное 2,72; "s" - среднеквадратичное отклонение; "s2" называют дисперсией.
Формула (3) носит название нормального закона распределения или закона Гаусса и полностью определяется заданием параметров
" а " и "s".
На рисунке (1) изображена функция w (x) для различных значений параметров " а " и "s". Величина "а" представляет собой значение координаты " х ", для которой w (x) достигает максимума. Величина "s" связана с величиной интервала х, в пределах которого
заключено 0.68 всех измеренных значений " х ".
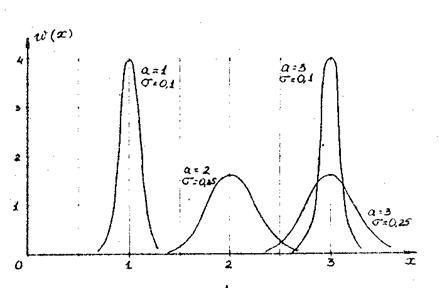 Рис.1 Функция распределения w(x) для разных значений среднего значения «а» и величины среднеквадратичного отклонения σ
Рис.1 Функция распределения w(x) для разных значений среднего значения «а» и величины среднеквадратичного отклонения σ
Основная задача измерений, при которых сказывается влияние случайных ошибок, состоит в том, чтобы определить значение искомой величины "а" и интервала разброса результатов измерения
Предполагая, что закон распределения случайных величин, кА
Такими можно считать результаты отдельных измерений, является нормальным, в теории вероятностей доказывается, что в качестве наивероятнейшей оценки истинного значения измеряемой величины "а" следует брать среднеарифметическое из результатов "n" измерений (3)
Для расчёта второго параметра нормального закона распределения - дисперсии - следует воспользоваться формулой:
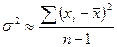 (6)
(6)
Таким образом, из формулы (6) видно, что с увеличением числа измерений n вероятность отклонения величины дисперсии от её истинного значения уменьшается с увеличением числа измерений. Проведя несколько десятков измерений получим достаточно точное значение для дисперсии всей совокупности проведённых измерений. В теории вероятностей доказывается, что при этом погрешность оценки истинного значения определяемой величины "а" по формуле (3) связана с величиной дисперсии всей совокупности измерений следующим соотношением:
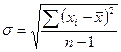 (7)
(7)
Здесь обозначено: s - среднеквадратичное отклонение для оценки величины "а" из произведённых измерений (по формуле (3
Величина s связана с интервалом 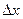 ,в котором находится р% всех измерений, как проведённых, так и последующих. Так например, при
,в котором находится р% всех измерений, как проведённых, так и последующих. Так например, при 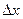 =
= 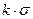 в интервал
в интервал 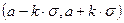 при:
при:
к = 1 попадает 68,3 % всех измерений
к = 2 попадает 95,4 % всех измерений
к = 3 попадает 99,7 % всех измерений.
Величину 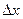 называют доверительным интервалом, а соответствующую долю Р всех измерений, попадающих в доверительный интервал
называют доверительным интервалом, а соответствующую долю Р всех измерений, попадающих в доверительный интервал 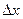 называют доверительной вероятностью.
называют доверительной вероятностью.
Выбор доверительной вероятности определяется целью измерений, т.е. тем, в какой степени нежелательны те случаи, когда истинное значение измеряемой величины выходит за пределы, полученные при оценке его доверительного интервала. Чем опаснее такие случаи, тем большую надёжность необходимо выбирать. У физиков принято приводить экспериментальные данные в виде плюс-минус одно среднеквадратичное отклонение, т.е.
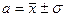 (8)
(8)
Такая запись удобна тем, что содержит обе величины: 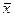 и s, но необходимо иметь в виду, что ей соответствует невысокая доверительная вероятность (68,3 %).Как правило, х и σ оцениваются из результатов эксперимента, и доверительная вероятность оказывается несколько ниже.
и s, но необходимо иметь в виду, что ей соответствует невысокая доверительная вероятность (68,3 %).Как правило, х и σ оцениваются из результатов эксперимента, и доверительная вероятность оказывается несколько ниже.
При малом числе измерений существует конечная вероятность того, что истинное значение среднеквадратичного отклонения отличается от вычисленного по формуле (7). Поэтому при небольшом числе измерений n пользоваться ею нецелесообразно и для оценки величины σ пользуются соотношениями, вытекающими из распределения Стьюдента, которое при неограниченном увеличении числа измерений стремится к нормальному распределению (3).
Часто при расчётах используют табличные данные: фундаментальные физические постоянные, различные характеристики веществ и значения различных функций. Если для них не указана точность (доверительный интервал), то в качестве абсолютной ошибки табличного значения берут половину единицы наименьшего разряда этой величины. Так, например, для расчёта сопротивления проводника из нихрома по таблицам находим, что его удельное сопротивление r = 1 * 10-6 Ом м, а для стали r = 1,0*10-7 Ом м. Так как в таблице не указаны доверительные интервалы, то для нихрома Dρ = 0,5*10-6 Ом м, а для стали Dρ = 0,05*10-7 Ом м.
Для часто используемого в расчётах значения p = 3,14 абсолютная ошибка составит Dp = 0,002, так как точное значение p = 3,1415926.... Используемое значение ускорения свободного падения на широте Москвы g = 9,819141  , округлённое до значения g = 9,8 м с-2, имеет Dg = 0,02 м с-2, а округлённое до значения g = 9,81 м с-2 имеет Dg = 0,009 м с-2.
, округлённое до значения g = 9,8 м с-2, имеет Dg = 0,02 м с-2, а округлённое до значения g = 9,81 м с-2 имеет Dg = 0,009 м с-2.
5. ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
И ПОСТРОЕНИЕ ГРАФИКОВ
Результаты измерений, проводимых в лаборатории, заносятся в таблицы, подготовленные в конспекте. В большинстве методических указаний приводится форма этих таблиц с указанием размерностей измеряемых величин. В тех случаях, когда таких готовых форм не приводится, студенту самостоятельно следует подготовить такую таблицу, имея в виду следующие соображения.
Число граф таблицы должно быть достаточным, чтобы можно было записать в них все измеряемые величины. В ряде случаев, некоторые графы-колонки для удобства работы в процессе измерений и последующей обработки результатов измерений разделяют на две (а при необходимости и на большее число) колонки, объединённые одним обозначением. Это делается в тех случаях, когда используется многопредельный прибор с изменяемым значение цены деления шкалы или в случае, когда цена деления не является простым целым числом, позволяющим быстро перевести деления шкалы в значение измеряемой величины.
К этим колонкам имеет смысл добавить графы для записи основных промежуточных результатов вычислений определяемой величины, а так же колонки для записи конечного, как правило, усреднённого результата.
В заголовке колонки приводится обозначение величины, используемое в расчётных формулах данного "Указания...".Единицы измерений должны соответствовать СИ с соответствующими допускаемыми приставками для кратных или дольных значений, таких
как "микро-", "милли-", "деци-", "кило-", "мега-" и т.п. При использовании множителей, не имеющих установленного наименования (например, 105, 10-7, 104 и т.д.) принято следующее соглашение. Если в заголовке графы стоит обозначение: "Т·104,К", то это означает, что в колонке записаны значения в 104 раз больше истинных; запись в заголовке "Т, 104 К" означает что записанные ниже величины приведены с десятитысячным множителем. Так например, цифра "375"
в колонке при способе записи "Т·104, К" означает: " Т = 0,0375 К". С другой стороны, при способе записи "Т, 104 К" та же самая цифра означает "Т =3750000 К".
Полученные экспериментальные результаты в ряде случаев лабораторной практики используются либо непосредственно, либо после предварительной обработки для построения графиков, необходимых для определения каких-либо других величин, не получаемых экспериментально, для установления эмпирических соотношений между какими-либо величинами, или для более наглядного представления полученных результатов. В большинстве случаев для построения графиков используется прямоугольная декартова система координат, в которой по оси абсцисс откладывается значение аргумента, а по оси ординат - значение функции. Для каждой оси устанавливается масштаб. Масштабные деления оцифровываются в соответствии с принятым рядом: 1, 2, 5. При необходимости применяют множитель в виде 10n. Начало отсчёта по каждой из осей не обязательно должно начинаться с нуля: диапазон масштабных значений должен соответствовать диапазону полученных экспериментальных значений аргумента и функции.
Полученные экспериментальные значения аргумента и функции откладываются на координатных осях в соответствии с выбранным масштабом. Пересечение перпендикуляров к осям, восстановленных в отмеченных положениях, даёт точку, обозначающую экспериментальный результат. Сами перпендикуляры при этом не рисуют. Поскольку экспериментальные результаты (точки) с неизбежностью содержат ошибки, то график не обязательно должен проходить через все эти точки. Существуют строгие математические методы, позволяющие построить по полученным экспериментальным
данным график зависимости с учётом условий проведённого эксперимента. В простейшем случае график проводится таким образом, чтобы число точек, лежащих выше и ниже линии было примерно одинаковым, а алгебраическая сумма их отклонений от проведённой линии приближалась к нулю. При соответствующем навыке построения графиков эта линия довольно близка к её аналитическому выражению, полученному строгими математическими методами.
В заключение отметим, что координатные оси и экспериментальные точки наносят простым карандашом, а все надписи и числовые и буквенные обозначения пишут ручкой. Это же правило относится к оформлению рисунков, схем и таблиц. При изображении электрических и кинематических схем необходимо использовать принятые в Единой Системе Конструкторской Документации (ЕСКД) изображения их элементов и правила оформления чертежей, изучаемые в курсе инженерной графики.
6. РАСЧЁТ ОШИБОК ПРЯМЫХ ИЗМЕРЕНИЙ
Если проведение неоднократных измерений физической величины даёт повторяющиеся результаты, то это означает, что в данных условиях преобладают приборные погрешности. В этих случаях погрешность прямых измерений определяется приборной погрешностью.
Если неоднократные измерения дают некоторый разброс результатов, то это означает присутствие случайных ошибок. Если число измерений неограниченно возрастает, то для определения среднего значения и дисперсии можно воспользоваться формулами (3)... (7). На практике число измерений всегда ограничено, поэтому существует конечная вероятность того, что истинное значение среднеквадратичного отклонения отличается от вычисленного по формуле (6). Поэтому при небольшом числе измерений для оценки величины s
пользуются соотношениями, вытекающими из так называемого распределения Стьюдента, которое при неограниченном увеличении числа измерений стремится к нормальному распределению (5).
В соответствии с этой методикой сначала находится среднеарифметическое значение измеряемой величины по формуле (3).
Следующим шагом для оценки точности найденного среднеарифметического значения будет вычисление вспомогательной величины S:
 (9)
(9)
Из Таблицы 1 коэффициентов Стьюдента находим вспомогательный коэффициент a, зависящий от числа измерений n и доверительной вероятности Р. Этот коэффициент совместно с величиной S позволяет рассчитать доверительный интервал Dx.
Абсолютная погрешность значения искомой величины "а", найденной как среднеарифметическое из n измерений составит:
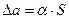 (10)
(10)
Искомая величина "а" представляется в виде:
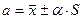 (11)
(11)
Дисперсия всей совокупности измерений случайной величины " х " будет равна S2.
7. РАСЧЁТ ОШИБОК КОСВЕННЫХ ИЗМЕРЕНИЙ
Пусть искомая величина А при выбранном методе косвенных измерений рассчитывается по формуле:
A = f (x 1, x 2, x 3,..., xn) (12)
где x1,x2,...,xn - величины, найденные в результате прямых измерений, с учётом ошибок о которых шла речь выше. Из-за этих ошибок величина " А " так же будет определяться с ошибками.
Пусть X 1, X 2,..., XN - значения f (x 1, x 2, x 3,..., xn), вычисленные для разных серий измерений (x 1, x 2,..., xn).
Таблица 1
Таблица коэффициентов Стьюдента
| Число измерений | Доверительная вероятность | |||||
| 0.7 | 0.8 | 0.9 | 0.95 | 0.99 | 0.999 | |
| 2.0 | 3.1 | 6.3 | 12.7 | 63.7 | 636.6 | |
| 1.3 | 1.9 | 2.9 | 4.3 | 9.9 | 31.6 | |
| 1.3 | 1.6 | 2.4 | 3.2 | 5.8 | 12.9 | |
| 1.2 | 1.5 | 2.1 | 2.8 | 4.6 | 8.6 | |
| 1.1 | 1.4 | 1.8 | 2.3 | 3.3 | 4.8 | |
| 1.1 | 1.3 | 1.8 | 2.1 | 3.0 | 4.1 | |
| 1.1 | 1.3 | 1.7 | 2.1 | 2.9 | 3.9 |
Абсолютной ошибкой косвенных измерений, по аналогии с абсолютной ошибкой прямых измерений, называют разность между истинным значением "А" и её значениями, полученными в результате измерений:
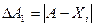 (13)
(13)
Размерность абсолютной ошибки совпадает с размерностью определяемой величины. Относительной ошибкой косвенных измерений называют отвлечённое число:
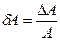 (14)
(14)
Иногда относительную ошибку выражают в процентах:
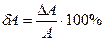 (15)
(15)
Для определения величины "А" в формулах (12)...(15) по теории
вероятностей следует брать величину Х, которую можно определить двумя способами:
1) А = Х = (Х 1 + Х 2 +...+ Хn)/ n (16)
2) A = X = f (x 1 + x 2 +...+ xn) (17)
где x 1, x 2,..., xn определяют по формуле (3). Если ошибки измерений малы, то оба способа дают практически тождественные результаты.
Рассмотрим способы нахождения ошибки величины А, определённой из косвенных измерений, по найденным значениям оши
бок прямых измерений. Выше отмечалось, что возможны различные соотношения между приборной систематической и случайными ошибками.
1-й случай. Преобладают приборные ошибки. В этом случае можно дать только оценку максимальной ошибки. Формулы для нахождения предельной ошибки косвенных измерений по внешнему виду совпадают с формулами дифференциального исчисления. В связи с этим для предельной абсолютной ошибки используется формула:
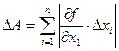 (18)
(18)
а для расчёта предельной относительной ошибки пригодна фор
- 19 -
мула:
 (19)
(19)
Формулы для расчёта предельных ошибок некоторых часто встречающихся функций, когда приборные ошибки превышают случайные, приведены в Таблице 2. Эти выражения легко рассчитываются по формулам (18) и (19).
2-й случай. Преобладают случайные ошибки. Для определения среднеквадратичной ошибки теория вероятностей даёт следующую формулу:
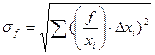 (20)
(20)
Относительная ошибка вычисляется по формуле:
 (21)
(21)
При выполнении промежуточных расчётов необходимо помнить, что число точных цифр в результате расчётов не может увеличиваться. Поэтому промежуточные результаты округляют, сохраняя
1...2 избыточных знака. При этом последующие цифры, меньшие
5,отбрасываются;если первая из отбрасываемых цифр больше 5,
то последняя из оставшихся цифр увеличивается на единицу. Ес
ли первая отбрасываемая цифра 5, то предыдущая цифра остаётся
без изменений, если она чётная, и увеличивается на единицу, если
она нечётная. Выражения для среднеквадратичной ошибки некоторых часто встречающихся функций приведены в Таблице 3. Для определения ошибок косвенных измерений используют большую из инструментальной или случайной ошибок прямого измерения.
8. ЗАПИСЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
При записи окончательного результата следует указывать:
- среднее значение измеряемой величины, найденное по формуле (3) или (10)
- доверительный интервал и доверительную вероятность, если при измерениях преобладают случайные ошибки, или максимальную ошибку, если при измерениях преобладают приборные и методические ошибки
- размерность измеренной величины.
Форма записи результатов:
а) преобладают приборные ошибки:
 , (размерность)
, (размерность)
или
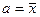 (размерность), δ = ….%
(размерность), δ = ….%
Таблица 2
| Функция | Абсолютная ошибка ΔY | Относительная ошибка δY |
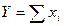
| 
| 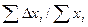
|

| 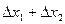
| 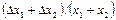
|

| 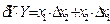
| 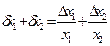
|
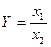
| 
| 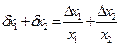
|
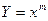
| 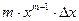
| 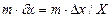
|

| 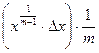
| 
|
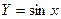
| 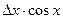
| 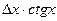
|
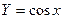
| 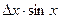
| 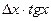
|
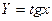
| 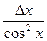
| 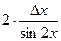
|
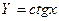
| 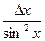
| 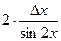
|
б) преобладают случайные ошибки:
 , (размерность)
, (размерность)
где р - доверительная вероятность; Δ x - доверительный интервал или
 (размерность), δ = ….%
(размерность), δ = ….%
Для косвенных измерений, так же как и для прямых, можно пользоваться понятием доверительной вероятности и доверительного интервала. Если число измерений всех переменных одинаково, то доверительный интервал и доверительная вероятность определяются как и в случае прямых измерений с тем же числом измерений. В случае разного числа измерений доверительный интервал и доверительная вероятность определяются по наименьшему числу измерений.
Если в записи отсутствует указание доверительной вероятности,
то это означает, что W = p = 0,68 и Δ x = σ.
Поскольку ошибки определяются по формулам, которые справедливы при большом числе измерений, то очевидно, что при небольшом числе измерений существует конечная погрешность в определении ошибок измерений. Условились, что при числе измерений n <10 для ошибки Δ x брать одну значащую цифру; при числе измерений n >(8...10) можно брать две значащие цифры при условии, что первая из них меньше 4.
СПИСОК ЛИТЕРАТУРЫ
1. Дж.Тейлор. Введение в теорию ошибок. М., «Мир»,1985.
2. Щиголев Б.М. Математическая обработка наблюдений. М.,1969. 344 с.
3. Зайдель А.Н. Ошибки измерений физических величин.Л.,1974.
Дата добавления: 2015-10-30; просмотров: 95 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| VIII. Write an essay on the topic “My biography”. Speak on the topic learnt. | | | EUNICE MOUNTAIN |