Структуры и алгоритмы

Читайте также:

ОБРАБОТКИ ДАННЫХ

курс лекций для студентов II курса

специальности

Программное Обеспечение

Вычислительной Техники и Автоматизированных Систем

ЧАСТЬ 1

МИИТ, 2006 год

Содержание.

Последовательное представление линейных списков
Связанное представление линейных списков
Очередь
Стек
Связанное представление матриц	7 – 8
Бинарное дерево поиска. Построение и поиск элемента	9 – 10
Бинарное дерево поиска. Удаление элемента	11 – 12
АВЛ – дерево. Построение и поиск элемента
АВЛ – дерево. Удаление элемента
В – дерево. Построение и поиск элемента
В – дерево. Удаление элемента	16 – 17
Линейные списки с индексами. Построение и поиск элемента. Коррекция
Инвертированные списки
Построение словаря с использованием деревьев	20 – 21
Построение словаря с использованием матриц
Хеш – таблицы. Функции расстановки
Хеш – таблицы. Способы разрешения коллизий

Последовательное представление линейных списков

Последовательные линейные списки – это просто одномерные или двумерные массивы. Например: задан массив A из N чисел.

…

Единственное достоинство такой структуры данных – это то, что, когда известен номер элемента, легко вычислить его адрес по формуле: , где - количество байт, занимаемых одним элементом.

Для оценки структуры данных существуют количественные показатели:

1. 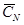- среднее количество сравнений при поиске элементов среди множества из N элементов.

2. - количество сравнений при поиске элемента, если его нет во множестве.

3. - среднее количество перемещений элементов при вставке и удалении элементов.

Рассмотрим данные характеристики применительно к последовательным линейным спискам:

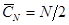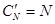; ; Ø; - самые плохие характеристики.

Последовательный линейный список имеет смысл употреблять, когда он упорядочен по возрастанию или убыванию. Здесь потребуется дополнительная работа по сортировке и применению алгоритма поиска. Но в данном случае характеристики значительно улучшатся:

; - самые лучшие; .

Связанное представление линейных списков

Связанные линейные списки – это списки, в которых элементы располагаются не подряд.

x₄

x₂

x₁

x₃

Однонаправленный список – динамическая структура данных вида:

Каждый элемент содержит информационное поле и указатель на следующий элемент. Поле ссылки последнего элемента имеет NIL. Информационное поле содержит ключ, идентифицирующий элемент списка, и, возможно, другую информацию.

Двунаправленный список – динамическая структура данных вида:

Каждый элемент включает в себя информационное поле, ссылку на следующий элемент и ссылку на предыдущий элемент.

Характеристика: Ø.

Очередь

First In First Out (FIFO). Заранее выделяется память из N-последовательных ячеек. Существуют два индекса:

HEAD – номер первого элемента очереди;

TAIL – последний элемент очереди.

Структура очереди:

Заказ, поступающий в очередь первым, выбирается первым для обслуживания. Пользователю доступны начало и конец очереди. Начало – позиция, из которой выбирается элемент. Конец – позиция, в которую помещается заносимый в очередь элемент.

Алгоритм постановки элемента в очередь:

Если TAIL=0 и HEAD=0, то очередь пуста. TAIL:=TAIL+1; Q(TAIL):=X; HEAD:=1. Если TAIL<>0, то очередь уже существует. TAIL=(TAIL+1)_mod _N. Если при этом TAIL=HEAD, то очередь переполнена. Q(TAIL):=X

Выбор элемента из очереди:

Если TAIL=0 и HEAD=0, то очередь пуста. Если очередь не пуста, то Y:=Q(HEAD); HEAD:=(HEAD+1)_mod _N.

Связанное представление очереди:

XN X

HEAD TAIL

Если head=nil, то очередь пуста

y:=head^.info;

head:=head^.link;

Постановка элемента в очередь:

Если очередь пуста, то вставляемый элемент будет первым.

p:=head; dispose(p); new(p); head:=p; tail:=p; p^.info:=x; p^.link:=nil;

new(p); p^.info:=x; p^.link:=nil; tail^.link:=p; tail:=p;

Стек

Last In First Out (LIFO). Существует индекс TOP – последний элемент стека.

Структура стека:

Доступна только вершина стека. Вершина стека – это позиция, в которой находится последний по времени поступления элемент. Выбирать элемент можно только из вершины стека. Выбранный элемент исключается из стека, а в его вершине оказывается элемент, который был занесен в стек перед выбранным элементом.

Алгоритм записи элемента в стек:

Если TOP=0, то стек пуст. TOP:=TOP+1. Если TOP>N, то стек переполнен. S(TOP):=X.

Алгоритм выбора элемента из стека:

Если TOP=0, то стек пуст. Y:=S(TOP); TOP:=TOP – 1.

Связанное представление стека:

TOP

Запись элемента в стек:

Если очередь пуста, то вставляемый элемент будет первым.

Внесение элемента в стек:

procedure InStack(var st: point; a: value);

var

q: point;

begin

new(q);

q^.inf:=a;

q^.next:=st;

st:=q;

end;

Выбор элемента из стека:

procedure OutStack(var st: point; var a: value);

var

q: point;

begin

if st=nil then writeln(‘Стек пуст’)

else

begin

a:=st^.inf;

q:=st;

st:=st^.next;

dispose(q);

end;

Связанное представление матриц

Рассмотрим такую структуру данных, как двунаправленный список.

Предположим, что задана матрица A(N×M), где N - количество строк, M - количество столбцов.

А₁₁	А₁₂	А₁₃
А₂₁	А₂₂	А₂₃

В памяти матрица описывается либо построчно, либо по столбцам, но чаще всего применяется построчное описание.

Существует связанное представление матриц. Если в двумерном списке содержится много пустых значений или нулей, то их удобно хранить в виде связанного представления.

i	j
А_ij	LINKD	LINKR

type

link=^node;

node=record

i: integer;

j: integer;

pole: integer;

linkd: link;

linkr: link

end;

Операции, производимые над матрицами: сложение, перемножение, транспонирование. Разумеется, эти операции удобнее выполнять над последовательными списками.

Рассмотрим для примера линейный однонаправленный список.

На рис.1 приведена структура однонаправленного списка. На нем поле INF – информационное поле, NEXT – указатель на следующий элемент списка. Список имеет особый элемент head, называемый указателем начала списка или головой списка, который обычно по формату отличен от остальных элементов. В поле указателя последнего элемента списка находится специальный признак nil, свидетельствующий о конце списка.

Рис.1

Элемент ЛОС имеет следующую структуру:

type

point = ^element; { указатель в списке }

element = record { элемент списка }

inf:integer;{ информационная часть }

next:point; {указатель на следующий элемент}

end;

Алгоритм вставки:

Вставкапроизводится в конец списка. Для этого необходимо пройти весь список:

Если список пустой: if p=nil then

Тогда создаём новый указатель на начало списка – head, и присваиваем информационному полю введённое число, а ссылке на следующий элемент – nil:

new(head);

head^.inf:=key;

head^.next:=nil

Если список не пустой, то перебираем все элементы списка пока поле next<>nil:

while p^.next<>nil do p:=p^.next;

Создаём новый указатель, указателю на следующий элемент присваиваем nil, а в последнем элементе списка в поле next записываем адрес нового указателя.

new(r);

r^.inf:=key;

r^.next:=nil;

p^.next:=r

Алгоритм поиска:

Поискпроизводитсяперебором всех элементовЛОС до тех пор, пока не будет найден элемент или пока не конец списка:while(p<>nil) or (p^.inf<>key) do p:=p^.next

Алгоритм удаления:

Удаление так же производится перебором всех элементов ЛОС. Удаляются все одинаковые элементы. Если удаляемый элемент первый в списке то указателю head присваивается значение поля next, а сам элемент удаляется:

head:=p^.next;

dispose(p);

Если элемент не первый то полю next предыдущего элемента присваивается значение поля next удаляемого элемента, а сам элемент удаляется:

if q^.inf=key then

p^.next:=q^.next;{p-предыдущий элемент}

dispose(q);

Бинарное дерево поиска. Построение и поиск элемента

На рис.1 приведена структура БДП, а на рис.2 – структура отдельного узла дерева. На рис.2 поле Inf – информационное поле, поле Left – указатель на «потомка» слева, Right – указатель на «потомка» справа. Стоит отметить, что в БДП не может быть одинаковых ключей.

Рис.1 Рис.2

right

inf

left

Структура БДП:

type

point = ^element; {указатель в списке }

element = record {элемент списка }

inf: integer; {информационная часть }

left, right: point {указатели на «потомков»}

end;

Построение дерева:

Осуществляется путем ввода элементов с информационными ключами, на основании которых строится дерево.Для включения вершины в дерево прежде всего нужно найти в дереве ту вершину, к которой можно присоединить новую вершину. При этом упорядоченность ключей должна сохраняться. Нужная вершина в дереве ищется по ключу который нужно вставить. Пусть построено некоторое дерево и требуется найти звено с ключом X. Сначала сравниваем с X ключ, находящийся в корне дерева. В случае равенства вставка невозможна. В противном случае переходим к рассмотрению вершины, которая находится слева внизу, если ключ X меньше только что рассмотренного, или справа внизу, если ключ X больше только что рассмотренного. Сравниваем ключ X с ключом, содержащимся в этой вершине, и т.д. Процесс завершается в одном из двух случаев:

· найдена вершина, содержащая ключ, равный ключу X;

· в дереве отсутствует вершина, к которой нужно перейти для выполнения очередного шага поиска (указатель = NIL).

В первом случае вставка невозможна. Во втором случае будет найдена вершина, к которой нужно присоединить данный ключ. Для вставки используется рекурсивная функция.

На PASCAL это выглядит следующим образом:

procedure Insert(var p: point; inf: integer; var f: boolean);

begin

f:=false;

if p=nil then

begin

new(p);

p^.key:=inf;

p^.left:=nil;

p^.right:=nil;

end

else

if inf<p^.key then Insert(p^.left,inf,f)

else

if inf>p^.key then Insert(p^.right,inf,f)

else

if inf=p^.key then f:=true;

end;

Поиск элемента:

Нужная вершина в дереве ищется по ключу. Поиск в бинарном дереве осуществляется следующим образом:

Пусть построено некоторое дерево и требуется найти звено с ключом X. Сначала сравниваем с X ключ, находящийся в корне дерева. В случае равенства поиск закончен и нужно возвратить указатель на корень в качестве результата поиска. В противном случае переходим к рассмотрению вершины, которая находится слева внизу, если ключ X меньше только что рассмотренного, или справа внизу, если ключ X больше только что рассмотренного. Сравниваем ключ X с ключом, содержащимся в этой вершине, и т.д. Процесс завершается в одном из двух случаев:

· найдена вершина, содержащая ключ, равный ключу X. Тогда возвращается указатель на найденную вершину.

· в дереве отсутствует вершина, к которой нужно перейти для выполнения очередного шага поиска.

На PASCAL это выглядит следующим образом:

function Search(inf: integer; p: point): point;

begin

while (p<>nil) and (p^.key<>inf) do

if p^.key<inf then p:=p^.right

else p:=p^.left;

Search:=p;

end;

Бинарное дерево поиска. Удаление элемента

Рис.1 Рис.2

right

inf

left

Структура БДП:

type

point = ^element; {указатель в списке }

element = record {элемент списка }

inf: integer; {информационная часть }

left, right: point {указатели на «потомков»}

end;

Удаление элемента:

При удалении сначала осуществляется поиск удаляемой вершины. При этом возможны три случая:

· Удаляемый элемент лист. В этом случае узел просто удаляется.

· Узел имеет одного сына. Тогда родительскому указателю присваивается значение сына, а сам элемент удаляется из памяти.

· Узел имеет двух сыновей. В этом случае в левом поддереве ищем самый правый узел (узел r), его ключ присваиваем полю inf удаляемого узла. Правой ссылке родительского узла элемента R присваиваем значение левой ссылки элемента r и удаляем из памяти узел R. Или в правом поддереве ищем самый левый узел (узел L), его ключ присваиваем полю inf удаляемого узла. Левой ссылке родительского узла элемента L присваиваем значение правой ссылки элемента L и удаляем из памяти узел L.

На PASCAL это выглядит следующим образом:

procedure DeleteNode (x:integer; var p:point);

var

q:point;

procedure Del (var r:point);

begin

if r^.right=nil then

begin

q^.inf:=r^.inf;

q:=r;

r:=r^.left;

end

else Del(r^.right);

end;

begin

if p=nil then

begin

writeln('Удаление. Элемент',x,'не найден');

readkey;

end

else

if x<p^.inf then DeleteNode(x, p^.left)

else

if x>p^.inf then DeleteNode(x, p^.right)

else

begin

q:=p;

if q^.right=nil then p:=q^.left

else

if q^.left=nil then p:=q^.right

else Del(q^.left);

dispose(q);

writeln('Удаление. Элемент ',x,' успешно удалён');

readkey;

end;

АВЛ – дерево. Построение и поиск элемента

АВЛ – бинарное дерево, для любой вершины которого разность высот левого и правого поддеревьев не превышает единицы (Сбалансированные по высоте деревья).

Построение:

Пусть даны ключи в последовательности 4, 5, 7, 2, 1, 3, 6 тогда построение такое:

Построение выполняется путём балансировки дерева.

Поиск:

Нужная вершина в дереве ищется по ключу.

1. Найдена вершина, содержащая ключ, равный ключу X;

2. В дереве отсутствует вершина, к которой нужно перейти для выполнения очередного шага поиска.

В первом случае возвращается указатель на найденную вершину.

АВЛ – дерево. Удаление элемента

Удаление:

При удалении сначала осуществляется поиск удаляемой вершины. Возможны следующие случаи:

1. Удаляемый элемент лист. В этом случае узел просто удаляется, производим балансировку дерева.

2. Узел имеет двух сыновей. В этом случае в левом поддереве ищем самый правый узел (узел r), его ключ присваиваем полю inf удаляемого узла. Правой ссылке родительского узла элемента r присваиваем значение левой ссылки элемента r и удаляем из памяти узел r., балансируем дерево.

В – дерево. Построение и поиск элемента

Механизм классических B-деревьев был предложен в 1970 г. Бэйером и МакКрейтом. B-дерево порядка n представляет собой совокупность иерархически связанных страниц внешней памяти (каждая вершина дерева – страница), обладающая следующими свойствами:

1. Каждая страница содержит не более 2*n элементов (записей с ключом).

2. Каждая страница, кроме корневой, содержит не менее n элементов.

3. Если внутренняя (не листовая) вершина B-дерева содержит m ключей, то у нее имеется m+1 страниц-потомков.

4. Все листовые страницы находятся на одном уровне.

Пример B-дерева степени 2 глубины 3 приведен на рисунке:

Классическое B-дерево порядка 2

Поиск:

Предположим, что происходит поиск ключа K. В основную память считывается корневая страница B-дерева. Предположим, что она содержит ключи k1, k2,..., km и ссылки на страницы p0, p1,..., pm. В ней последовательно (или с помощью какого-либо другого метода поиска в основной памяти) ищется ключ K. Если он обнаруживается, поиск завершен. Возможны три ситуации:

1. Если в считанной странице обнаруживается пара ключей ki и k(i+1) такая, что ki < K < k(i+1), то поиск продолжается на странице pi.

2. Если обнаруживается, что K > km, то поиск продолжается на странице pm.

3. Если обнаруживается, что K < k1, то поиск продолжается на странице p0.

Для внутренних страниц поиск продолжается аналогичным образом, пока либо не будет найден ключ K, либо мы не дойдем до листовой страницы. Если ключ не находится и в листовой странице, значит ключ K в B-дереве отсутствует.

В – дерево. Удаление элемента

B-дерево порядка n представляет собой совокупность иерархически связанных страниц внешней памяти (каждая вершина дерева - страница), обладающая следующими свойствами:

Каждая страница содержит не более 2*n элементов (записей с ключом).

Каждая страница, кроме корневой, содержит не менее n элементов.

Если внутренняя (не листовая) вершина B-дерева содержит m ключей, то у нее имеется m+1 страниц-потомков.

Все листовые страницы находятся на одном уровне.

Пример B-дерева степени 2 глубины 3 приведен на рисунке:

Классическое B-дерево порядка 2

Удаление элемента:

Различают два случая - удаление ключа из листовой страницы и удаления ключа из внутренней страницы B-дерева. В первом случае удаление производится просто: ключ просто исключается из списка ключей. При удалении ключа во втором случае для сохранения корректной структуры B-дерева его необходимо заменить на минимальный ключ листовой страницы, к которой ведет последовательность ссылок, начиная от правой ссылки от ключа K (это минимальный содержащийся в дереве ключ, значение которого больше значения K). Тем самым, этот ключ будет изъят из листовой страницы

Начальный вид B-дерева

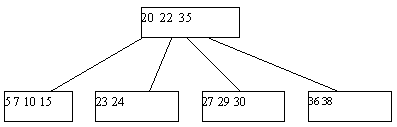
B-дерево после удаления ключа 25

Поскольку в любом случае в одной из листовых страниц число ключей уменьшается на единицу, может нарушиться требование, что любая, кроме корневой, страница B-дерева должна содержать не меньше n ключей. Если это случается, начинает работать процедура переливания ключей. Берется одна из соседних листовых страниц (с общей страницей-предком); ключи, содержащиеся в этих страницах, а также средний ключ страницы-предка поровну распределяются между листовыми страницами, и новый средний ключ заменяет тот, который был заимствован у страницы-предка.

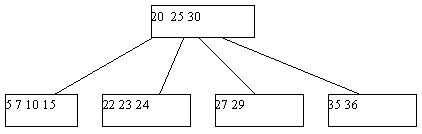
Результат удаления ключа 38 из B-дерева

Может оказаться, что ни одна из соседних страниц непригодна для переливания, поскольку содержат по n ключей. Тогда выполняется процедура слияния соседних листовых страниц. К 2*n-1 ключам соседних листовых страниц добавляется средний ключ из страницы-предка (из страницы-предка он изымается), и все эти ключи формируют новое содержимое исходной листовой страницы. Поскольку в странице-предке число ключей уменьшилось на единицу, может оказаться, что число элементов в ней стало меньше n, и тогда на этом уровне выполняется процедура переливания, а возможно, и слияния. Так может продолжаться до внутренних страниц, находящихся непосредственно под корнем B-дерева. Если таких страниц всего две, и они сливаются, то единственная общая страница образует новый корень. Высота дерева уменьшается на единицу, но по-прежнему длина пути до любого листа одна и та же.
Начальный вид B-дерева

B-дерево после удаления ключа 29

Линейные списки с индексами. Построение и поиск элемента. Способы коррекции

Это последовательные списки, то есть массивы. Обязательно рассортируем их в порядке возрастания. Массив N делят на секции, размер каждой из которых N/I, где I – число секций. Для этой таблицы строится таблица индексов. В ней I строк и 2 столбца. В одном столбце записывается максимальный ключ секции, в другом – адрес начала секции, то есть номер первого элемента секции, а номер – это индекс.

В таблице индексов I строк. Количество строк равно количеству секций. Всего 2 столбца. В одном столбце записывается max путь, в другом адрес начала этой секции.

Алгоритм поиска элемента с номером k. Ищем в таблице индексов до тех пор, пока ключ k больше ключа в этой таблице. Находим начало секции, в которой нужно искать этот ключ. Перебираем, пока не найдем ключ.

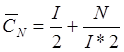
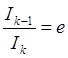
Для данного примера составим таблицу индексов:



	∞

Коррекция линейного списка:

Удаление элемента. Удаляемый элемент просто помечается.

Вставка элемента. Приходится осуществлять передвижку элементов. Чтобы уменьшить количество передвижек, придумали следующий способ: При первоначальном заполнении каждая секция заполняется не полностью, остается место. Однако, может получиться, что в какой-то момент времени секция получится полностью заполненной. Если такое случится, то проводится операция реорганизации: все помеченные элементы удаляются, свободное пространство из всех секций суммируется и делится поровну между всеми секциями.

Инвертированные списки

Инвертированный список – это таблица, в которой столько строк, сколько значений имеет поле, по которому построен инвертируемый список и два столбца. 1 – значения поля 2 – значение адреса записей в исходной таблице, в которых имеется это значение.

Коррекция инвертированных списков:

Если в исходную таблицу добавляется новый элемент, то он будет записан последним.

Инвертированные списки очень похожи на линейные списки с индексами. Они отсортировывают по значению поля. Над ними можно строить таблицы индексов.

Современные базы данных автоматически составляют список по всем полям.

Построение словаря с использованием деревьев

Пусть задана некоторая последовательность значений, которые могут повторяться. Необходимо подсчитать, сколько раз каждое значение входит в последовательность. Иначе говоря, нужно построить словарь. (Например, для заданного текста подсчитать, сколько раз входит в него каждое из слов).

Если диапазон возможных значений в последовательности конечен и не слишком велик, то это можно сделать с помощью массива, каждый элемент которого представляет собой счетчик для соответствующего значения. Для каждого очередного значения последовательности увеличивается значение его счетчика. Однако если диапазон возможных значений бесконечен или конечен, но слишком велик (например, количество разных слов в тексте), то мы не можем использовать массив, так как неизвестна его длина. В этом случае задача построения частотного словаря может быть решена с помощью дерева поиска.

К каждому узлу дерева добавляется поле счетчика. Для каждого очередного значения в последовательности осуществляется его поиск в дереве. Если такого значения в дереве еще нет (то есть оно встретилось в первый раз), в дереве создается узел, полю счетчика которого присваивается значение 1. Если узел с таким значением найден (значение встретилось уже не в первый раз), то поле счетчика этого узла увеличивается на 1.

После завершения последовательности значений можно выполнить b-обход построенного дерева, распечатывая для каждого узла его значение и величину счетчика, в результате чего получим отсортированный частотный словарь. Рассмотрим процедуру построения такого дерева на примере подсчета частного словаря символов некоторого текста. (Конечно, такую задачу можно решить и с помощью массива, так как количество разных символов в тексте конечно и невелико, но для примера рассмотрим ее решение с помощью дерева поиска).

type ptr = ^node; node = record info: char; count: integer; llink, rlink: ptr; end;procedure InsertAndCount(x: char; var p: ptr);begin if p=nil then begin new(p); p^.info:= x; p^.count:= 1; p^.llink:= nil; p^.rlink:= nil; end else if x<p^.info then InsertAndCount(x, p^.llink) else if x>p^.info then InsertAndCount(x, p^.rlink) else p^.count:= p^.count+1;end;

Для последовательности символов фразы <построение частотного словаря> (без учета пробелов) будет построено следующее дерево:

Выполнив b-обход этого дерева, получим словарь:

Символ

Частота

Построение словаря с использованием матриц

В таблице должно быть столько столбцов сколько букв в исходном алфавите + 1 столбец, номер + 1 столбец, пробел + 1столбец пояснение. Количество строк произвольно. Для ускорения поиска номера столбца по букве используется Хеш-таблица. Известно, что каждая буква кодируется, и ей соответствует какое-то десятичное число. Код «Я» - 64, значит, в Хеш-таблице будет 64 строки.

Адрес буквы:

Удаление слова из словаря:

Находим слово и записываем путь. Если строка не пустая, то это конец. Хорошо было бы строки, освободившиеся от значений удалённых слов использовать для записи новых слов.

Для этого соединили их в целую цепочку свободных строк. При поиске, свободные строки берём из цепочки. Среднее количество сравнений при поиске слова равно средней длине слова, то есть равно L.

Хеш – таблицы. Функции расстановки

Хеш-таблица – это обычный массив с необычной адресацией, задаваемой хеш-функцией, например: адрес = ключ mod 10. На рис.1 представлена хеш-таблица, не содержащая ни одного элемента. На рис.2 представлена хеш-таблица с элементами (адрес = ключ mod 10).

Рис.1 Рис.2


		-1
	-1	-1
-1	-1	-1
-1	-1	-1
	-1	-1
-1	-1	-1
-1	-1	-1
		-1
	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

Расстановка в хеш-таблице ключей. Для включения ключа в хеш-таблицу, сначала вычисляется адрес ключа. Если хотя бы одна ячейка строки свободна, тогда ключ просто помещается в свободную ячейку. Если все ячейки заняты тогда, возникает коллизия. В случае коллизии проверяем все ячейки по строкам. Если какой-нибудь ключ не совпадает с адресом, то вместо него помещается исходный ключ, а для другого ключа ищем свободную ячейку. Если все ячейки заняты по праву, то перемещаемся по порядку по всем ячейкам, пока значение не станет равно -1. Если найдено значение -1, то помещаем ключ в эту ячейку

Хеш – таблицы. Способы разрешения коллизий

Рис.1 Рис.2


		-1
	-1	-1
-1	-1	-1
-1	-1	-1
	-1	-1
-1	-1	-1
-1	-1	-1
		-1
	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

Разрешение коллизий происходит путём:

1. Линейного опробования. Идём до тех пор, пока не найдётся первое свободное место -1 куда и запишем ключ.

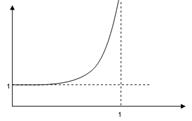
Количество сравнений зависит от

2. Случайное опробование – если при вычислении адреса получим коллизию, то берём другую форму для вычисления, если и там получим коллизию, то разрешим её методом линейного опробования.

3. Срастающиеся цепочки: Если получим коллизию, то ищем свободное место, помещаем на него элемент и соединим его цепочкой с предыдущим элементом.

Дата добавления: 2015-10-30; просмотров: 97 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>

Похідний стрій | Незвичайний день звичайного хлопчика Дениса

mybiblioteka.su - 2015-2024 год. (0.073 сек.)

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

<== предыдущая страница	\|	следующая страница ==>
Похідний стрій	\|	Незвичайний день звичайного хлопчика Дениса

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1

-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1
-1	-1	-1