Характеристическое рентгеновское излучение

Характеристическое рентгеновское излучение имеет не сплошной, а линейчатый спектр. Этот тип излучения возникает, когда быстрый электрон, достигая анода, проникает во внутренние орбитали атомов и выбивает один из их электронов. В результате появляется свободное место, которое может быть заполнено другим электроном, спускающимся с одной из верхних атомных орбиталей. Такой переход электрона с более высокого на более низкий энергетический уровень вызывает рентгеновское излучение определенной дискретной длины волны. Поэтому характеристическое рентгеновское излучение имеет линейчатый спектр. Частота линий характеристического излучения полностью зависит от структуры электронных орбиталей атомов анода.
Линии спектра характеристического излучения разных химических элементов имеют одинаковый вид, поскольку структура их внутренних электронных орбитальных идентична. Но длина их волны и частота, благодаря энергетическим различиям между внутренними орбиталями тяжелых и легких атомов.
Частота линий спектра характеристического рентгеновского излучения изменяется в соответствие с атомным номером металла и определяется уравнением Мозли: v^1/2= A (Z-B), где Z - атомный номер химического элемента, A и B - константы.

96. Радиоуглерод-радиоактивный нуклид химического элементауглерода с атомным номером 6 и массовым числом 14.Углерод-14 является одним из природных радиоактивных изотопов. Период его полураспада, составляющий 5730±30 лет, Наиболее часто используется в ледниковой и постледниковой геологии, в археологии, а также в физике атмосферы, геоморфологии, гляциологии, гидрологии и почвоведении, в физике космических лучей, физике Солнца и в биологии, не только для датировок, но и как трассер различных природных процессов. Углерод-14 образуется в верхних слоях тропосферы и стратосферы в результате поглощения атомами азота-14 тепловых нейтронов, которые в свою очередь являются результатом взаимодействия космических лучей и вещества атмосферы:

СВОЙСТВА НЕЙТРИНО----Существуют три типа (аромата) нейтрино – электронное (νe), мюонное (νμ) и таонное (ντ). Масса мала (< 1эВ), но существует. Время жизни: > 1010 сек × mν (возможно бесконечное), mν - масса в эВ.Электрический заряд меньше 10-17 e, возможно равен нулю. Спин – ½. Cпин нейтрино направлен против направления движения, cпин антинейтрино направлен по направлению движения. Нейтрино разных ароматов могут переходить друг в друга – осцилляция нейтрино. Магнитный момент нейтрино меньше 10-12 магнитного момента электрона, но по-видимому, не равен нулю. Возможна прецессия в сильных магнитных полях.---- Гипотеза (принцип запрета) Паули фундаментальная гипотеза квантовой механики, согласно которой две тождественные частицы с полуцелым спином, т. е. фермионы (например, два электрона в атоме), не могут одновременно находиться в одном и том же состоянии, т. е. не могут описываться или располагать одинаковым набором квантовых чисел.

Теория ядра приводила к

заключению, что спин исходного ядра в единицах h/2p должен выражаться целым

числом. Между тем спин электрона равен половине, а орбитальный момент

количества движения электронов мог быть только целым числом h/2p. Поэтому

получалось, что в результате b-распада целый спин ядра должен был бы

переходить в полуцелый и наоборот. Это означало нарушение закона сохранения

момента количества движения.

99. Осуществить незатухающую цепную реакцию можно несколькими основными путями^[5]:

Увеличить объём образца (для выделенного из руды урана возможно достижение критической массы за счёт увеличения объёма);

Осуществить разделение изотопов, повысив содержание ²³⁵U в образце;

Сократить потерю свободных нейтронов через поверхность образца с помощью применения различного рода отражателей;

Использовать замедлитель для повышения концентрации тепловых нейтронов.

Критическая масса — в ядерной физике минимальное количество делящегося вещества, необходимое для начала самоподдерживающейсяцепной реакции деления. Коэффициент размножения нейтронов в таком количестве вещества больше единицы или равен единице. Размеры, соответствующие критической массе, также называют критическими.

101. фазовое пространство-- пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.

Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки. Кроме того, в механике движение этой точки определяется сравнительно простыми уравнениями Гамильтона, анализ которых позволяет делать заключения о поведении сложных механических систем.

102.Физическая статистика изучающая свойства вырожденных коллективов, называется квантовой статистикой. Задачей физической статистики является отыскание неивероятнейшего распределения частиц по энергиям, импульсам и т.д. Электроны, образующие электронный газ в кристаллах, то своим свойствам отличаются от молекул обычного газа, поэтому и законы распределения этих частиц по состоянием различны. Молекулярный газ, подчиняющийся классической статистики Максвела-Больцмана; электронный газ квантовой статистики Ферми-Дерака. Квантовая статистика Ферми-Дерака исходит из: 1) Электроны, образующие электронный газ, обладают волновыми свойствами => подчиняются законам квантовой механики => их энергия, импульсы, могут иметь только определенные дискретные значения, причем каждому такому значению энергии или импульса отвечает строго определенное квантовое состояние системы. 2) Частицы, образующие электонный газ, тождественны друг другу, и перестановка их местами не приводит к появлению нового микросостояния системы. 3) Электроны, образующие электронный газ, подчиняются принципу Паули (в одном квантовом состоянии может находится не более 2-х электронов с противоположно направленными спинами).

103. Функция f(E,T) называется функцией Ферми. Эта функция определяется вероятностью того, что квантовые состояния с энергией Е заняты частицами при заданной температуре Т. По её смыслу её не может быть больше единицы.
Параметр системы частиц EF, входящий в выражение для функции Ферми, носит название энергии Ферми (энергию Ферми называют также химическим потенциалом), а соответствующее значение по лекалу энергий называется энергией Ферми.
Формально, исходя из (10), энергию Ферми можно определить как энергию таких квантовых состоянии, вероятность заполнения которых частицами равна 0,5. Действительно, из (10) следует, что f(EF,T) =0,5.
Энергия Ферми квантовой системы фермионов зависит от

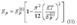
концентрации частиц n0 и от температуры Т, а значение энергии Ферми при абсолютном нуле температуры (здесь и далее абсолютный нуль температуры понимается как предел Т=>0, имеется в виду, что абсолютный нуль недостижим) можно рассматривать по формуле

.
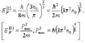
Обычно рассматриваются системы, у которых 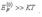. Для таких систем cогласно (1) можно пренебречь зависимостью энергии Ферми от температуры и считать
Вид функции Ферми приведен на рисунке.
полностью заполненные частицами, а все квантовые состояния с энергией - 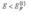пустые. Поэтому энергию Ферми при абсолютном нуле можно определить как максимальную энергию частиц данной системы при T=00K. За счет нагрева системы часть частиц имевших при T=00K энергии меньше уровня Ферми приобретают энергии несколько выше уровня Ферми. При этом область частично заполненных квантовых состояний, т.е. область, где, 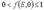, имеет по шкале энергий размер порядка 2КТ.

104.Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии (kT << DE), то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному.

105.

В этой теории, учитывается вырождение электронного газа, учитываются волновые свойства электронов, а движение электронов проводимости в металлах расматривается как процесс распространения электронных волн, длинна которых определяется формулой Де Бройля λ(инд.e)=h/mv. На основе квантовой статистики Ферми-Дерака можно найти:

δкв=e(c.2)nλ(в)(М)/mv(в)(М). В классической формуле v(в) – средняя энергия теплового движения электронов проводимости, v(в)~T(c.1/2). В квантовой формуле v(в)(М) – скорость электронов, обладающих энергией Ферми => она не зависит от температуры, т.к. энергия Ферми есть величина постоянная для данного проводника. Однако самое большое различие между формулами заключается в том, какой физический смысл вносит та и другая теория в длинну свободного пробега электронов λ. В классической теории причина сопротивления движению электронов проводимости в металлах объясняется столкновением электрона проводимости с узлами кристаллической решетки, при этом каждый электрон сталкивается со всеми узлами на своем пути, поэтому λ равна постоянной кристаллической решетки d. Квантовая теория учитывает волновые свойства электронов, а движение электрона проводимости в кристалле рассматривает как процесс распространения электронных волн, длина которых определяется формулой деБройля. Идеальные кристаллические решетки не должны расеивать электронных волн. Рассеяние элетронных волн возникает с появлением центров рассеяния по величине превосходящих длину электронных волн. Такими центрами рассеивания могут являться неоднородности в кристалле, которые возникают за счет тепловых колебаний узлов решетки. Т.е. в любой момент времени кристалл является микроскопически неоднородным за счет флуктуацияй плотности, по объему превосходящих длину электронных волн, и является эффективными центрами рассеивания электронных волн. Именно они являются причиной сопротивления абсолютно (химически) чистых металлов. Рассеивающая способность металла может быть определена с помощью коэффициента рассеивания

η(инд.T) ~ 1/λ(в). С другой стороны коэффициент рассеивания можно определить η(инд.Т)=πnkT/Ed; n – концентрация электронного газа в металле, d – постоянная решетки; λ(в)=Ed/πnkT; λ(в)~T(c.-1); δкв~T(c.-1). Это согласуется с экспериментальными данными.

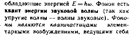
106.

Собственный полупроводник или полупроводник i-типа или нелегированный полупроводник (англ. intrinsic — собственный) — это чистый полупроводник, содержание посторонних примесей в котором не превышает 10⁻⁸ … 10⁻⁹%. Концентрация дырок в нём всегда равна концентрации свободных электронов, так как она определяется не легированием, а собственными свойствами материала, а именно термически возбуждёнными носителями, излучением и собственными дефектами.

Полупроводник без примесей обладает собственной электропроводностью, которая имеет два вклада: электронный и дырочный. Если к полупроводнику не приложено напряжение, то электроны и дырки совершают тепловое движение и суммарный ток равен нулю. При приложении напряжения в полупроводнике возникает электрическое поле, которое приводит к возникновению тока, называемого дрейфовым током i_др. Полный дрейфовый ток является суммой двух вкладов из электронного и дырочного токов:

i_др= i_n+ i_p,

где индекс n соответствует электронному вкладу, а p - дырочному. Удельное сопротивление полупроводника зависит от концентрации носителей и от их подвижности, как следует из простейшей модели Друде. В полупроводниках при повышении температуры вследствие генерации электрон-дырочных пар концентрация электронов в зоне проводимости и дырок ввалентной зоне увеличивается значительно быстрее, нежели уменьшается их подвижность, поэтому с повышением температуры проводимость растет. Процесс гибели электрон-дырочных пар называется рекомбинацией. Фактически проводимость собственного полупроводника сопровождается процессами рекомбинации и генерации и если скорости их равны, то говорят что полупроводник находится в равновесном состоянии. Количество термически возбуждённых носителей зависит от ширины запрещённой зоны, поэтому количество носителей тока в собственных полупроводниках мало по сравнению с легированными полупроводниками и сопротивление их значительно выше.

108.

Т.к. в собственных ПП концентрация электронов и дырок

одинакова n(инд.i)=p(инд.i), то расчет показывает, что M(инд.i)=(-Eo/2). Т.е. уровень Ферми находятся точно посередине запрещенной зоны. Если температура низка, то

энергия теплового возбуждения kT

мала, kT<<Eo, и ее недостаточно

для переброса электронов из

валентной зоны в зону проводимости,

но достаточно

для перевода электронов с донорного

уровня в зону

проводимости или из валентной зоны на

акцепторный уровень.

В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис. 316). Действительно, для переброса электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачивается энергия активации, равная ширине запрещенной зоны D E. При появлении же электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия, затраченная на образование пары носителей тока, должна делиться на две равные части. Так как энергия, соответствующая половине ширины запрещенной зоны, идет на переброс электрона и такая же энергия затрачивается на образование дырки, то начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от кото­рой происходит возбуждение электронов и дырок.

Вывод о расположении уровня Ферми в середине запрещенной зоны собственного полупроводника может быть подтвержден математическими выкладками. В физике твердого тела до­казывается, что концентрация электронов в зоне проводимости

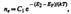
где E ₂ — энергия, соответствующая дну зоны проводимости (рис. 316), Е_F — энергия Ферми, Т — термодинамическая температура, С ₁ — постоянная, зависящая от температуры и эффективной массы электрона проводимости. Эффективная масса — величина, имеющая размерность массы и характеризующая динамические свойства квазичастиц — электронов проводимости и дырок. Введение в зонную теорию эффективной массы электрона проводимости позволяет, с одной стороны, учитывать действие на электроны проводимости не только внешнего поля, но и внутреннего периодического поля кристалла, а с другой стороны, абстрагируясь от взаимодействия электронов проводимости с решеткой, рассматривать их движение во внешнем поле как движение свободных частиц.

Концентрация дырок в валентной зоне

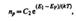
где С ₂ — постоянная, зависящая от температуры и эффективной массы дырки, Е ₁ — энергия, соответствующая верхней границе валентной зоны. Энергия возбуждения в данном случае от­считывается вниз от уровня Ферми (рис. 316), поэтому величины в экспоненциальном множителе (242.3) имеют знак, обратный знаку экспоненциального множителя в (242.2). Так как для собственного полупроводника п_e=n_p (242.1), то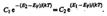

Если эффективные массы электронов и дырок равны (), то С ₁ =С ₂ и, следовательно, – (E ₂ –E_F) = =E ₁ –E_F, откуда

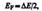
т. е. уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны.

109.

В собственных ПП проводимость осуществляется электронами и дырками, поэтому δ=δ(инд.э)+δ(инд.д). Проводимость опеределяется концентрацией носителей и их подвижностью. δ(инд.э)=e*n(инд.i)*U(инд.n);

δ(инд.д)=e*p(инд.i)*U(инд.p); n(инд.i)=p(инд.i); δ=e*n(инд.i)*(U(инд.n) +

+ U(инд.p); Согласно расчетам U=A*T(c. –3/2), A – const; A(инд.n)=A(инд.р); U(инд.n)=A(инд.n)*T(c. –3/2); U(инд.p)=A(инд.p)*

T(c. –3/2); n(инд.i)=B*e(c. -∆E(инд.о)/2kT); ∆Е(инд.о) – энергия активации собственной проводимости. Т.к. концентрация

носителей в собственном ПП меняется

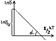с температурой по сильному

экспоненциальному закону, а

подвижность по отношению

слабому степенному, то

удельная проводимость меняется

с температурой также,

как и концентрация. δ=δ(инд.о)*e(c. - ∆Eo/kT);

lnδ=lnδ(инд.о) - ∆E/2kT; tgα=∆Eo.

Дата добавления: 2015-10-23