Дві різні площини α і βпаралельні до площини γ. Доведіть, що площини α і β паралельні. Варіант 13

Читайте также:

Діагностична контрольна робота з геометрії

Клас

Контрольна робота містить 20 варіантів. Кожен із них складається з трьох частин, які відрізняються складністю та формою тестових завдань.

У І частині контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки одна правильна. Завдання вважається виконаним правильно, якщо учень записав тільки літеру, якою позначено правильний варіант відповіді. Правильна відповідь за кожне із п’яти завдань оцінюється одним балом.

ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.

ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис з обґрунтуванням. Правильне розв’язання завдання оцінюється трьома балами.

Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожної частини (5; 4; 3–всього 12балів).

Контрольна робота розрахована на 45 хвилин. Роботи виконуються у зошитах або на окремих аркушах. При виконанні роботи необхідно вказати номер завдання. Текст завдань переписувати не обов’язково.

Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності.

Зразок підпису роботи

Діагностична контрольна робота

з геометрії

учня (учениці) 11_____ класу

______________________________

назва навчального закладу

______________________________

прізвище ім’я в родовому відмінку

Варіант _____

Звіт з математики

Місто (район)_________________________________________

Табл.1. Кількісний звіт

Кількість учнів	Писало	Результати
І рівня	ІІ рівня	ІІІ рівня	ІV рівня
кількість	%	кількість	%	кількість	%	кількість	%

Табл.2. Якісний звіт

Всього учнів

Писало

Правильна відповідь завдань у %

Кількість набраних балів у %

Кількість учнів

6 завдання

7 завдання

8 завдання

Аналітичний звіт: матеріал, засвоєний учнями якісно; допущені типові помилки, причини та шляхи їх подолання.

Примітка. Якщо до тексту завдань були внесені корективи, то необхідно надіслати змінені тексти з обґрунтуванням необхідності такого кроку.

Виконавець підпис прізвище, ініціали

Варіант 1

І частина (5 балів)

Завдання 1 – 5 мають по чотири варіанти відповіді, з яких тільки одна правильна. Оберіть правильну, на Вашу думку, відповідь. Правильне розв’язання кожного завдання оцінюється одним балом.

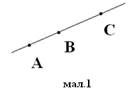1. Скільки площин можна провести через точки А, В, С? (мал. 1)

А) одну; Б) дві;

В) безліч; Г) не можна визначити.

2. Укажіть геометричну фігуру, якою може бути проекція ромба при паралельному проектуванні.

А) трапецією; Б) трикутником; В) точкою; Г) відрізком.

3. На малюнку КО α, ОВ а. Порівняйте довжини відрізків КА і КВ (мал. 2)

А) КА<КВ; Б) КА=КВ;

В) КА>КВ; Г) не можна визначити.

4. Точка М належить площині грані АВСD прямокутного паралелепіпеда АВСDA₁B₁C₁D₁ (мал. 3). Знайдіть кут між прямими A₁D₁ і СМ, якщо кут ВСМ дорівнює 140º.

А) 40º; Б) 50º;

В) 90º; Г) 140º.

5. Ортогональною проекцією многокутника площею S є многокутник площею S₁ = 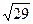. Яке з чисел не може бути значенням параметра S?

А) 6; Б) 5; В) 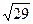; Г) 29.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Бісектриса одного з кутів паралелограма точкою перетину ділить сторону на два рівних відрізки довжиною 15 см. Знайдіть периметр паралелограма.

7. Побудуйте переріз піраміди SABC площиною, що проходить через точки M, K, P, що належать ребрам SA, SB, AC відповідно.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Дано трикутник АВС, в якому АВ = 9 см, ВС = 12 см, АС = 15 см. На стороні АВ взято точку М так, що АМ: МВ = 2: 1. Через точку М проведено площину, яка паралельна стороні АС і перетинає сторону ВС в точці К. Знайдіть площу трикутника МВК.

Варіант 2

І частина (5 балів)

1. Скільки площин можна провести через точки А, В, С (мал. 1)?

А) одну; Б) дві;

В) безліч; Г) не можна визначити.

2. Укажіть геометричну фігуру, якою не може бути проекція кола при паралельному проектуванні.

А) відрізком; Б) точкою; В) еліпсом; Г) колом.

3. На мал. 2 АВ - дотична до кола з центром у точці О, точка В - точка дотику, ОС (АОВ), довжина відрізка ОС дорівнює радіусу кола. Знайдіть кут між площинами АВС і АОВ.

А) 90º; Б) 60º;

В) 45º; Г) 30º.

4. Площа трикутника дорівнює 24 см², а його ортогональної проекції - см². Знайдіть кут між площиною проекції та площиною даного трикутника.

А) 60º; Б) 30º; В) 90º; Г) 45º.

5. Відрізок NB - перпендикуляр до площини правильного трикутника АВС, М - середина сторони АС (мал. 3). Укажіть кут між площинами АNС і АВС.

А) NBM; Б) NAB;

В) NCB; Г) NMB.

ІІ частина (4 бали)

6. Довжина кола, вписаного у рівнобічну трапецію, дорівнює 12π см. Обчисліть площу трапеції, якщо різниця основ цієї трапеції дорівнює 10 см.

7. Через вершину В рівнобедреного трикутника АВС (АВ = ВС) до площини трикутника проведено перпендикуляр BD довжиною 5 см. Знайдіть відстань від точки D до сторони АС, якщо АС = 8 см, АВ = 6 см.

ІІІ частина (3 бали)

8. Доведіть, що коли площина перетинає площину трапеції по прямій, яка містить її середню лінію, то вона паралельна основам трапеції.

Варіант 3

І частина (5 балів)

1. Скільки спільних точок має площина α і площина, яка проходить через точку А і пряму (мал. 1)?

А) одну; Б) дві;

В) безліч; Г) три.

2. Якою фігурою може бути паралельна проекція квадрата на площину?

А) трикутником; Б) трапецією;

В) паралелограмом; Г) точкою.

3. На мал.2 КО α, ОВ а. Порівняйте довжини відрізків КА і КС.

А) КА < КС; Б) КА = КС;

В) КА > КС; Г) не можна визначити.

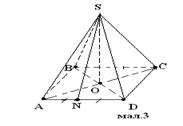4. На мал.3 зображено правильну чотирикутну піраміду SABCD. SO - висота. Якою є градусна міра кута між площинами SOA і SOD?

А) 45°; Б) 30°;

В) 60°; Г) 90°.

5. Ортогональною проекцією многокутника площею S = є многокутник площею S₁. Яке з чисел не може бути значенням параметра S₁?

А) 3; Б) 5; В) 7; Г) 9.

ІІ частина (4 бали)

6. Катет прямокутного трикутника дорівнює 30 см, а гіпотенуза відноситься до другого катета як 17: 8. Знайдіть сторони трикутника.

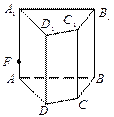7. Побудуйте переріз прямої призми ABCDA₁B₁C₁D₁ площиною, що проходить через вершини С, D₁та точку F на ребрі АА₁.

ІІІ частина (3 бали)

8. Дано трикутник АВС, в якому АВ = 16 см, АС = 12 см, ВС = 20 см. На стороні АВ взято точку М так, що ВМ: МА = 3: 1. Через точку М проведено площину, яка перетинає сторону АС в точці К. Знайдіть площу трикутника АМК, якщо відомо, що дана площина паралельна ВС.

Варіант 4

І частина (5 балів)

1. Дано дві прямі a і b, що перетинаються. Через точку А, яка лежить на прямій а, проведено пряму с паралельно прямій b. Скільки різних площин можна провести через ці три прямі?

А) одну; Б) дві; В) три; Г) жодної.

2. Якою фігурою може бути паралельна проекція прямокутника на площину?

А) трикутником; Б) трапецією; В) відрізком; Г) точкою.

3. На мал.1 точка О-центр вписаного в трикутник АВС кола, ОМ (АВС), ОК АС. Відстані від точки М до точок А і К дорівнюють a і b відповідно. Порівняйте величини a і b, якщо це можливо.

А) ; Б) ;

В) ; Г) порівняти неможливо.

4. Точка М належить площині грані АВСD прямокутного паралелепіпеда АВСDA₁B₁C₁D₁ (мал. 2). Знайдіть кут між прямими A₁В₁ і СМ, якщо кут ВСМ дорівнює 140º.

А) 40°; Б) 50°;

В) 90°; Г) 140°.

5. Площа ортогональної проекції чотирикутника дорівнює 24 см². Кут між площиною проекції та площиною даного чотирикутника становить 60°. Знайдіть площу чотирикутника.

А) 48 см²; Б) 18 см²; В) 20 см²; Г) 62 см².

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. Кути ромба відносяться як 1: 3, а його сторона дорівнює 8 см. Знайдіть площу ромба.

7. Площина перетинає сторони АВ і АС трикутника АВС в точках В₁ та С₁ відповідно. АС₁: С₁С = 3: 2 та В₁С₁ = 5 см. Знайдіть довжину відрізка ВС, якщо ВС ׀׀ .

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Вершина С рівностороннього трикутника АВС, сторона якого 8 см, віддалена від площини α на відстань см. Обчисліть кут між площинами трикутника АВС і α, якщо сторона АВ лежить у площині α.

Варіант 5

І частина (5 балів)

1. Які з наведених нижче тверджень правильні:

1) якщо пряма перетинає дві основи трапеції, то вона лежить у площині цієї трапеції;

2) якщо діаметр круга належить площині, то всі точки круга належать цій площині?

А) жодне; Б) лише перше; В) лише друге; Г) обидва.

2. Точки К і М є серединами ребер PB і PC тетраедра PABC (мал. 1). Якій із зазначених площин паралельна пряма МК?

А) РАВ; Б) РВС;

В) РАС; Г) АВС.

3. Пряма ОМ перпендикулярна до площини кола з центром в точці О. Знайдіть радіус кола ОВ, якщо МВ = 12 см, ОМВ=30°.

А) 12; Б) ; В) ; Г) 6.

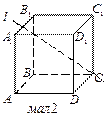4. Дано куб АВСDA₁B₁C₁D₁і пряму l, яка проходить через вершину С і середину ребра A₁B₁ (мал. 2). Яку із зазначених прямих перетинає пряма l?

А) DD₁; Б) ВС; В) ВB₁; Г) AD.

5. Пряма АК проходить через вершину А трикутника АВС, АК АВ і АК АС. Який кут утворює пряма АК із площиною трикутника АВС?

А) 90⁰; Б) 60⁰;

В) 30⁰; Г) визначити неможливо.

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 може мати короткий запис без обґрунтування. Правильне розв’язання кожного завдання оцінюється двома балами.

6. За координатами середин сторін трикутника (5; 1), (9; −2), (9; 4) визначте довжини його сторін.

7. Сторона АВ трикутника АВС лежить в площині . Площина , яка є паралельною до , перетинає сторони АС та ВС в точках А₁ та В₁ відповідно. Знайдіть довжину відрізка А₁В₁, якщо А₁С = 9 см, АА₁ = 3 см, АВ = 8 см.

ІІІ частина (3 бали)

Розв’язання 8 завдання повинно мати обґрунтування. Потрібно записати послідовні логічні дії та пояснення. Правильне розв’язання завдання оцінюється трьома балами.

8. Рівнобічну трапецію, периметр якої дорівнює 48 см, а гострий кут 60^о, розташовано в площині α. Точка М однаково віддалена від усіх сторін трапеції і знаходиться на відстані 3 см від площини α. Знайдіть відстань від цієї точки до сторін трапеції.

Варіант 6

І частина (5 балів)

1. Які з наведених нижче тверджень правильні:

1) якщо пряма перетинає дві діагоналі трапеції, то вона лежить у площині цієї трапеції;

2) якщо три вершини ромба належать площині, то всі точки ромба належать цій площині?

А) жодне; Б) лише перше; В) лише друге; Г) обидва.

2. Точки К і М є серединами ребер PB і ВC тетраедра PABC відповідно (мал. 1). Якій із зазначених площин паралельна пряма МК?

А) РАВ; Б) РВС;

В) РАС; Г) АВС.

3. На мал.2 ВО α, ВС a. Яке співвідношення правильне?

А) ; Б) ;

В) ; Г) неможливо визначити.

4. АВСDA₁B₁C₁D₁ - куб. Виберіть пряму, яка із прямих є мимобіжною з прямою DA.

А) АВ; Б) ВB₁; В) B₁C₁; Г) СВ.

5. У правильній трикутній піраміді SABC SO - висота, точка N належить ребру SB, N₁ - проекція точки N на площину основи піраміди. Визначить вид кута NN₁B.

А) прямий; Б) тупий; В) гострий; Г) не можна визначити.

ІІ частина (4 бали)

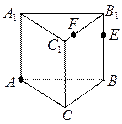6. Вершини трикутника знаходяться в точках (5; 1), (7; 2), (9; −2). Який вид має даний трикутник?

7. Побудуйте переріз прямої призми ABCA₁B₁C₁ площиною, що проходить через вершину А та точки Е та F, які лежать на ребрах ВВ₁ та В₁С₁ відповідно.

ІІІ частина (3 бали)

8. Трапеція є вписаною в коло, причому менша її основа, що дорівнює 16 см, стягує дугу в 60^о. На відстані 12 см від площини трапеції знаходиться точка, рівновіддалена від всіх вершин трапеції. Знайдіть відстань від цієї точки до вершин трапеції.

Варіант 7

І частина (5 балів)

1. Які з наведених нижче тверджень правильні:

1) якщо площина паралельна двом діагоналям ромба, то вона паралельна його площині;

2) якщо пряма паралельна двом різним площинам, то ці площини паралельні?

А) жодне; Б) лише перше; В) лише друге; Г) обидва.

2. На мал.1 зображено куб і позначено три точки. Одна точка є серединою ребра куба, а дві інші розміщені у його вершинах. Укажіть геометричну фігуру, яка є перерізом куба площиною, що проходить через ці точки.

А) правильний трикутник;

Б) трикутник, який не є правильним;

В) прямокутник, який не є квадратом;

Г) квадрат.

3. Скільки всього існує різних площин, які проходять через пряму і точку в просторі?

А) одна; Б) безліч; В) дві; Г) одна або безліч.

4. Відстань від точки М до сторін квадрата дорівнює 13 см. Знайдіть відстань від точки М до площини квадрата, якщо сторона квадрата дорівнює 10 см.

А) 8 см; Б) 11 см; В) 12 см; Г) 14 см.

5. SABCD – чотирикутна піраміда (мал. 2). Площини МНК і АВС паралельні. К − середина ребра SC. Оберіть правильну відповідь:

А) АМ = МS; Б) AM > MS;

В) AM < MS; Г) не можна порівняти.

ІІ частина (4 бали)

6. Діагональ ромба ділить його висоту, проведену з вершини тупого кута, на відрізки, які відносяться як 13: 5. Знайдіть цю висоту, якщо сторона ромба дорівнює 65 см.

7. Із точки до площини проведено дві похилі, довжини яких відносяться як 5: 6. Знайдіть відстань від точки до площини, якщо відповідні проекції похилих дорівнюють 4 см і 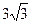см.

ІІІ частина (3 бали)

8. Кінці відрізка лежать у двох взаємно перпендикулярних площинах. Проекції відрізка на кожну із площин відповідно дорівнюють см і 20 см. Відстань між основами перпендикулярів, проведених із кінців відрізка до площин, дорівнює 12 см. Знайдіть довжину даного відрізка.

Варіант 8

І частина (5 балів)

1. Які з наведених нижче тверджень правильні:

1) якщо площина паралельна двом сторонам ромба, то вона паралельна його площині;

2) якщо пряма a паралельна площині трикутника АВС, то прямі а і АВ паралельні?

А) жодне; Б) лише перше; В) лише друге; Г) обидва.

2. На мал. 1 зображено куб і позначено три точки. Дві точки є серединами ребер куба, а третя розміщена у його вершині. Укажіть геометричну фігуру, яка є перерізом куба площиною, що проходить через ці точки.

А) паралелограм;

Б) трапеція;

В) тупокутний трикутник;

Г) прямокутний трикутник.

3. Дано дві площини α і β, які перетинаються. Точка М не належить жодній із них. Скільки існує прямих, які проходять через М і паралельні α і β?

А) жодної; Б) одна; В) безліч; Г) жодної або одна.

4. Відстань від точки М до всіх вершин квадрата дорівнює 5 см. Знайдіть відстань від точки М до площини квадрата, якщо його діагональ дорівнює 6 см.

А) 3 см; Б) 4 см; В) 2 см; Г) 8 см.

5. SABCD – чотирикутна піраміда (мал. 2). Площини PRQ і АВС паралельні. Порівняйте довжини відрізків АР і PS.

А) AP = PS; Б) AP > PS;

В) AP < PS; Г) не можна порівняти.

ІІ частина (4 бали)

6. У рівнобедреному трикутнику бісектриса кута при основі, ділить висоту, яка проведена до основи, на відрізки 20 см та 12 см. Знайдіть периметр трикутника.

7. Площини і паралельні. В площині вибрано точки M і N, а в площині − точки M₁ і N₁ такі, що прямі МM₁ і NN₁ паралельні. Знайдіть довжину відрізків NN₁ і M₁N₁, якщо MN = 5 см, МM₁ = 6 см.

ІІІ частина (3 бали)

8. Через гіпотенузу АВ прямокутного рівнобедреного трикутника АВС проведено площину β під кутом 45° до площини трикутника. Обчисліть кути нахилу катетів трикутника АВС до площини β.

Варіант 9

І частина (5 балів)

1. На мал. 1 зображено куб АВСDA₁B₁C₁D₁. Переріз куба площиною АСС₁ –це…

А) дві паралельні прямі;

Б) відрізок;

В) трикутник;

Г) прямокутник.

2. Як розміщені дві прямі, якщо їх проекції на площину паралельні?

А) перетинаються; Б) паралельні;

В) мимобіжні; Г) не можна визначити.

3. Укажіть пряму перетину площин АСК і АРВ на малюнку 2.

А) АК; Б) АВ;

В) АР; Г) РВ.

4. Точка, віддалена від усіх вершин прямокутного трикутника на 5 см, розміщена на відстані 2 см від площини трикутника. Знайдіть довжину гіпотенузи трикутника.

А) 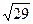см; Б) см; В) см; Г) см.

5. Площа трапеції дорівнює 40 см². Кут між площиною трапеції і площиною її проекції становить 60°. Знайдіть площу проекції трапеції.

А) 49 см²; Б) 18 см²; В) 20 см²; Г) 62 см².

ІІ частина (4 бали)

6. У коло вписані квадрат і правильний шестикутник. Периметр квадрата дорівнює 84 мм. Знайдіть периметр шестикутника.

7. Із точки, що знаходиться на відстані 4 см від площини, проведено до цієї площини дві похилі довжиною 5 см і см. Кут між проекціями цих похилих дорівнює 60^о. Знайдіть відстань між основами похилих.

ІІІ частина (3 бали)

8. Доведіть, що коли площина і пряма, яка не лежить у цій площині, паралельні одній і тій же площині, то вони паралельні між собою.

Варіант 10

І частина (5 балів)

1. На мал. 1 зображено прямокутний паралелепіпед АВСDA₁B₁C₁D₁. Переріз даного многогранника площиною, яка проходить через середини бічних ребер - це…

А) шестикутник; Б) прямокутник;

В) паралелограм; Г) відрізок.

2. Як розміщені два відрізка, якщо їх паралельні проекції на площину перетинаються?

А) перетинаються; Б) паралельні;

В) не перетинаються; Г) не можна. визначити.

3. На мал. 2 АВ − дотична до кола з центром у точці О, точка В − точка дотику, , відстань від точки С до прямої АВ дорівнює діаметру кола. Знайдіть кут між площинами АВС і АОВ.

А) 60º; Б) 30º;

В) 45º; Г) 90º.

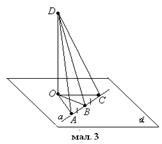
4. На мал. 3 DO α, OB a. Порівняйте довжини відрізків DA і DB.

А) DA > DB; Б) DA < DB;

В) DA = DB; Г) не можна визначити.

5. Площа ромба дорівнює 36 см², а кут між площиною його проекції та площиною ромба становить 60°. Знайдіть площу проекції ромба.

А) 49 см²; Б) 18 см²; В) 20 см²; Г) 62см².

ІІ частина (4 бали)

6. Діагональ рівнобічної трапеції дорівнює 12 см і перпендикулярна до бічної сторони, а також є бісектрисою кута при основі, що дорівнює 60^о. Обчисліть площу трапеції.

7. Із точки, що знаходиться на відстані 12 см від площини, проведені до цієї площини дві похилі довжиною 13 см і 20 см. Відстань між основами похилих дорівнює 19 см. Знайдіть кут між проекціями похилих.

ІІІ частина (3 бали)

8. Пряма b лежить в площині α. Пряма а не лежить в площиніα і паралельна прямій b. Через точку М, яка лежить в площині α (М b), проведено пряму с, паралельну а. Доведіть, що с лежить в площині α.

Варіант 11

І частина (5 балів)

1. Дано куб АВСDA₁B₁C₁D₁. Назвіть переріз куба, який проходить через ребро АА₁ і містить діагональ нижньої основи.

А) АA₁D₁D; В) АA₁C₁C;

Б) АA₁B₁B; Г) не можна визначити.

2. Площини і паралельні. Точка М не належить жодній з них. Скільки всього існує прямих, які проходять через М і паралельні площинам і ?

А) одна; Б) дві; В) безліч; Г) визначити неможливо

3. На мал.1 зображено трикутну піраміду SABC, у якої ASC=85°, SAC=65°. Площини MNL і SAC паралельні. Визначте NML.

А) 85°; Б) 65°;

В) 30°; Г) 150°.

4. Із точки А до площини проведено перпендикуляр і похилу, довжина якої 20 см. Кут між похилою і площиною 60°. Знайдіть довжину перпендикуляра.

А) 10 см; Б) см; В) см; Г) см.

5. Площа трикутника дорівнює 36 см², а його ортогональної проекції - 18 см². Знайдіть кут між площиною проекції і площиною даного трикутника.

А) 90°; Б) 60°; В) 45°; Г) 30°.

ІІ частина (4 бали)

6. Бічна сторона рівнобічної трапеції з кутом при основі 30^о дорівнює 10 см, а діагональ 25 см. Обчисліть площу трапеції.

7. Сторони трикутника АВС дорівнюють 10 см, 17 см і 21 см. Із вершини більшого кута трикутника до його площини проведено перпендикуляр АD, який дорівнює 15 см. Знайдіть відстань від точки D до сторони ВС трикутника.

ІІІ частина (3 бали)

8. Доведіть, що через дві мимобіжні прямі можна провести паралельні площини.

Варіант 12

І частина (5 балів)

1. Дано прямокутний паралелепіпед АВСDA₁B₁C₁D₁. Назвіть переріз паралелепіпеда, який проходить через ребро ВВ₁ і містить діагональ верхньої основи.

А) B₁ВСС₁; Б) B₁ВDD₁;

В) B₁ВAA₁; Г) не можна визначити.

2. Паралельною проекцією прямокутного трикутника АВС є відрізок А₁В₁, АВС=90°, АС = 6, ВС = 8. Паралельною проекцією точок А і С є точка А₁, а точки В - В₁. Знайдіть довжину проекції медіани СМ.

А) 3; Б) 6; В) 4; Г) 8.

3. Скільки різних площин можна провести через точки А, В і С, якщо АВ = 2 см, ВС = 2 см, АС = 2 см?

А) жодної; Б) дві; В) більше ніж дві; Г) одну.

4. На мал. 2 зображено правильну чотирикутну піраміду SABCD. SO - висота. Який кут є кутом між площинами грані SAD і основи АВСD?

А) SAC; Б) SNO;

В) SDB; Г) SCN.

5. Площина α перетинає відрізок АС у точці В, причому АВ: ВС = 2: 1 (мал.3). Через точки А і С проведено паралельні прямі, які перетинають площину α у точках А₁ і С₁ відповідно. Знайдіть периметр трикутника АВА₁, якщо периметр трикутника СВС₁ дорівнює 4.

А) 2; Б) 4;

В) 8; Г) 16.

ІІ частина (4 бали)

6. Дві хорди кола перетинаються. Одна з них ділиться точкою перетину на відрізки 3 см і 12 см, а друга — навпіл. Знайдіть довжину другої хорди.

Із даної точки до площини проведено дві похилі, різниця довжин яких дорівнює 6 см. Їх проекції на цю площину дорівнюють 27 см і 15 см. Знайдіть відстань від даної точки до площини.

ІІІ частина (3 бали)

Дві різні площини α і βпаралельні до площини γ. Доведіть, що площини α і β паралельні. Варіант 13

І частина (5 балів)

1. АВСDA₁B₁C₁D₁ – куб, пряма l проходить через вершину А₁ і середину ребра DC (мал. 1). Яку із зазначених прямих перетинає пряма l?

А) D₁D; Б) BС;

В) АA₁; Г) АD.

2. Які з тверджень є вірними:

1) пряма, що не лежить у площині трикутника, перетинає дві його сторони;

2) пряма не є паралельною площині на якій є прямі їй паралельні?

А) жодне; Б) перше; В) друге; Г) обидва.

3. Точка М рівновіддалена від вершин рівностороннього трикутника АВС (мал. 2), МО (АВС). Знайдіть довжину проекції похилої МВ на площину АВС, якщо сторона трикутника см.

А) 8 см; Б) 4 см;

В) 15 см; Г) см.

4. Відрізок АВ не перетинає площину β, А₁В₁ — проекція відрізка АВ на площину β, АА₁ = 4 см, ВВ₁ = 10 см. Знайдіть відстань від середини відрізка АВ до площини β.

А) 14 см; Б) 7 см; В) 6 см; Г) 3 см.

5. Площа трапеції дорівнює 48 см², а кут між площиною її ортогональної проекції і площиною трапеції становить 60°. Знайдіть площу проекції даної трапеції.

А) 96 см²; Б) 18 см²; В) 24 см²; Г) 62 см^2..

ІІ частина (4 бали)

6. Складіть рівняння кола, що проходить через початок координат і має центр у точці А (4; 3).

7. Через вершину А паралелограма АВСD проведено площину α. Через точки В, С і D проведено паралельні прямі, які перетинають α в точках В₁, С₁, D₁ відповідно. Знайдіть DD₁, якщо ВВ₁ = 4 см, СС₁ = 12 см.

ІІІ частина (3 бали)

8. Із середини М сторони АВ правильного трикутника АВС проведено до площини трикутника перпендикуляр МN; точка N сполучена з С. Доведіть, що СN АВ.

Варіант 14

І частина (5 балів)

1. Які з наведених нижче тверджень правильні:

1) дві площини паралельні одній і тій самій прямій паралельні між собою;

2) пряма має спільну точку з однією з паралельних площин і не перетинає другу?

А) жодне; Б) перше; В) друге; Г) обидва.

2. Через точку М, що належить ребру ВD тетраедра АВСD, проведено площину, паралельну площині АВС. У скільки разів площа трикутника АВС більша за площу перерізу тетраедра АВСD даною площиною, якщо DМ: МВ = 1: 3?

А) у 3 рази; Б) у 4 рази; В) у 9 разів; Г) у 16 разів.

3. ABCDA₁B₁C₁D₁ паралелепіпед. Площинам яких граней паралельна пряма AD?

А) ABB₁A₁; Б) DD₁C₁С; В) A₁B₁C₁D₁; Г) AB₁C₁D.

4. Квадрат перегнули по діагоналі ВD так, що площини АВD і СВD стали перпендикулярними. Знайдіть відстань між точками А і С, якщо сторона квадрата дорівнює 1.

А) ; Б) 1; В) 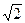; Г) 2.

5. Трикутник А₁В₁С₁ – проекція рівностороннього трикутника АВС. На стороні А₁В₁відмічені точки K, L, N так, що А₁К = KL = LN = NB₁. Укажіть проекцію висоти трикутника АВС, опущеної з вершини С.

А) С₁К; Б) С₁L;

В) C₁N; Г) задача має неоднозначну відповідь.

ІІ частина (4 бали)

6. Складіть рівняння кола що дотикається осі абсцис, якщо його центр знаходиться у точці А (1; 2).

7. Через вершину А паралелограма АВСD проведено площину α. Через точки В, С, D проведені паралельні прямі, які перетинають α в точках В₁, С₁ і D₁ відповідно. Знайдіть СС₁, якщо ВВ₁ = 3 см, DD₁ = 8 см.

IІІ частина (3 бали)

8. Відрізок ВМ перпендикулярний до площини прямокутника АВСD. Доведіть, що пряма СD перпендикулярна площині МВС.

Варіант 15

І частина (5 балів)

1. Точка О—центр правильного трикутника АВС, ОМ – перпендикуляр до площини АВС і ОМ = см, АО = 3 см. Знайдіть кут нахилу МА до площини трикутника АВС.

А) 60°; Б) 30º; В) 45°; Г) 90⁰.

2. Площина, перпендикулярна до катета АВ прямокутного трикутника АВС, перетинає його в точці М, а гіпотенузу АС — в точці N. Знайдіть МN, якщо АN = NС = 5, СВ = 6.

А) 3; Б) 4; В) 5; Г) 8.

3. Кінці відрізка АВ лежать у перпендикулярних площинах і β. Точка А віддалена від площини β на см, а точка В від площини – на см. Порівняйте значення параметрів і , якщо даний відрізок утворює кути 40º і 80º з площинами і β відповідно.

А) відповідь залежить від довжини відрізка АВ; Б) ;

В) ; Г) .

4. Яким може бути взаємне розташування двох прямих, одна з яких лежить в площині, а друга паралельна цій площині?

А) перпендикулярні; Б) паралельні;

В) паралельні або мимобіжні; Г) мимобіжні.

5. PАВСD – чотирикутна піраміда (мал. 1).Через точки С₁і С₂, що належать ребру PС, паралельно до площини АВР проведено площини і відповідно. Площі перерізів піраміди PАВСD цими площинами дорівнюють S₁ і S₂ відповідно. Порівняйте величини S₁ і S₂, якщо це можливо.

А) S₁ > S₂; Б) S₁ < S₂;

В) S₁ = S₂; Г) порівняти неможливо.

ІІ частина (4 бали)

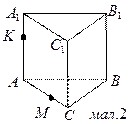6. У колі проведено дві хорди, що перетинаються. Одна з них ділиться точкою перетину на відрізки 2 см і 6 см, а довжина другої — 7 см. Знайдіть відрізки другої хорди.

7. Побудуйте переріз прямої призми АВСA₁B₁C₁ площиною, що проходить через точку B₁ та точки М і К, що лежать на ребрах АС і АА₁ відповідно.

ІІІ частина (3 бали)

Точка М знаходиться на відстані 3 см від кожної з вершин паралелограма, сторони якого відносяться як 2: 1. Знайдіть площу цього паралелограма, якщо відстань від точки М до площини паралелограма дорівнює 2 см. Варіант 16

І частина (5 балів)

1. Якщо одна з двох паралельних прямих перпендикулярна до третьої прямої, то як розташовано другу пряму по відношенню до третьої?

А) паралельна; Б) перпендикулярна;

В) мимобіжна; Г) співпадають.

2. АВСDA₁B₁C₁D₁ − куб. Укажіть пряму перетину площин DВA₁ і DВC₁.

А) АВ; Б) D₁B₁;

В) DВ; Г) АС.

3. Паралелограм АВСD і трапеція АDFK (АD׀׀FK) не лежать в одній площині. Як розташовані пряма ВС і площина АКF?

А) пряма лежить в площині;

Б) пряма та площина перетинаються;

В) пряма та площина паралельні;

Г) визначити неможливо.

4. Кінці відрізка віддалені від площини на 2 см та 8 см. Проекція його на площину дорівнює 8 см. Якою є довжина самого відрізка?

А) 2 см; Б) 8 см; В) 10 см; Г) 5 см.

5. На площині взято точку А (мал. 3). Знайдіть відстань від даної точки до прямої перетину площин і β, якщо дана точка віддалена від площини β на 4 см, а кут між площинами дорівнює 45º.

А) 4 см; Б) см;

В) 8 см; Г) см.

ІІ частина (4 бали)

6. У трикутнику, площа якого дорівнює 48 см², проведено середню лінію. Знайдіть площу трикутника, який утворився.

7. Точка М – середина ребра ВС піраміди SABC. Побудуйте переріз піраміди площиною, що проходить через точку М і паралельна площині ASC та знайдіть площу перерізу, якщо SA = 24 см, SC = 10 см, АС = 26 см.

ІІ частина (3 бали)

8. Ребро куба дорівнює а. Знайдіть найкоротшу відстаньміж діагоналлю куба і діагоналлю основи куба, які не мають спільних точок.

Варіант 17

І частина (5 балів)

1. Через точку D проведено пряму DС, перпендикулярну до площини прямокутного рівнобедреного трикутника АВС ( С=90º). Відстані від точки D до точок А і В дорівнюють а см і b см відповідно. Порівняйте значення параметрів а і b, якщо це можливо.

А) a = b; Б) a < b; В) a > b; Г) порівняти неможливо.

Дата добавления: 2015-10-30; просмотров: 349 | Нарушение авторских прав

Читайте в этой же книге: Командный зачет 1 дня | ИКАР Ставрополь 2 | Группа М40-50 | Командный зачет 2 дня |

<== предыдущая страница	\|	следующая страница ==>
My parents DON'T understand!	\|	Дві різні площини α і βпаралельні до площини γ. Доведіть, що площини α і β паралельні. Варіант 13

mybiblioteka.su - 2015-2024 год. (0.14 сек.)