
Читайте также:
|
103. Частная производная 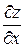 от функции
от функции  имеет вид:
имеет вид:
А) 1 Б) -1 В) 2 Г) 0 
104. Частная производная 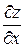 от функции
от функции 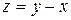 имеет вид:
имеет вид:
А) 0 Б) -1 В) 1 Г) 2
105. Частная производная 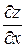 от функции
от функции 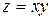 имеет вид:
имеет вид:
А) 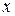 Б)
Б) 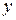 В)
В) 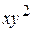 Г)
Г) 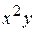
106. Частная производная 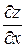 от функции
от функции 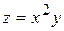 имеет вид:
имеет вид:
А) 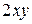 Б)
Б) 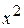 В)
В) 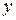 Г)
Г) 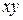
107. Частная производная 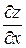 от функции
от функции 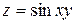 имеет вид:
имеет вид:
А) 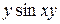 Б)
Б) 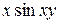 В)
В) 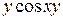 Г)
Г) 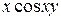
108. Частная производная 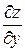 от функции
от функции 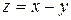 имеет вид:
имеет вид:
А) -1 Б) 1 В) 0 Г) 2
109. Частная производная 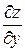 от функции
от функции 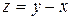 имеет вид:
имеет вид:
А) 1 Б) -1 В) 2 Г) 0
110. Частная производная 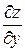 от функции
от функции 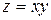 имеет вид:
имеет вид:
А) 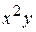 Б) y В) х Г)
Б) y В) х Г) 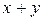
111. Частная производная 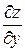 от функции
от функции 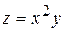 имеет вид:
имеет вид:
А) 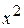 Б)
Б) 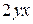 В)
В) 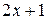 Г)
Г) 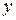
112. Частная производная 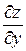 от функции
от функции 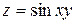 имеет вид:
имеет вид:
А) 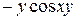 Б)
Б) 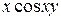 В)
В) 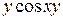 Г)
Г) 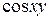
113. Дифференциал функции 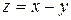 имеет вид:
имеет вид:
А) 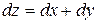 Б)
Б) 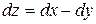 В)
В) 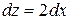 Г)
Г) 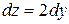
114. Дифференциал функции 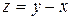 имеет вид:
имеет вид:
А) 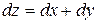 Б)
Б) 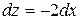 В)
В) 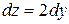 Г)
Г) 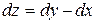
115. Дифференциал функции 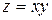 имеет вид:
имеет вид:
А) 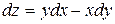 Б)
Б) 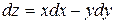
В) 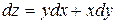 Г)
Г) 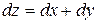
116. Дифференциал функции 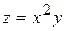 имеет вид:
имеет вид:
А) 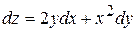 Б)
Б) 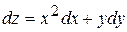
В) 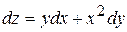 Г)
Г) 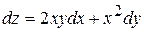
117. Дифференциал функции 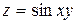 имеет вид:
имеет вид:
А) 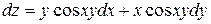 Б)
Б) 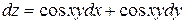
В) 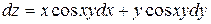 Г)
Г) 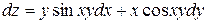
118. Частная производная 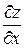 от функции
от функции 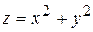 имеет вид:
имеет вид:
А) 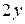 Б)
Б) 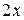 В)
В) 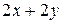 Г)
Г) 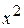
119. Частная производная 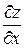 от функции
от функции 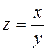 имеет вид:
имеет вид:
А) 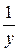 Б)
Б) 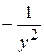 В)
В) 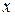 Г)
Г) 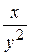
120. Частная производная 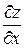 от функции
от функции 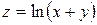 имеет вид:
имеет вид:
А) 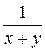 Б)
Б) 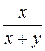 В)
В) 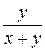 Г)
Г) 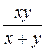
121. Частная производная 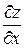 от функции
от функции 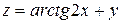 имеет вид:
имеет вид:
А) 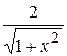 Б)
Б) 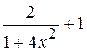 В)
В) 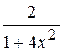 Г)
Г) 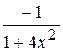
122. Частная производная 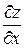 от функции
от функции 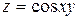 имеет вид:
имеет вид:
А) 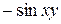 Б)
Б) 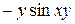 В)
В) 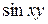 Г)
Г) 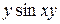
123. Частная производная 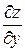 от функции
от функции 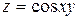 имеет вид:
имеет вид:
А) 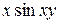 Б)
Б) 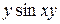 В)
В) 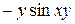 Г)
Г) 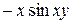
124. Частная производная 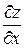 от функции
от функции 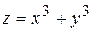 имеет вид:
имеет вид:
А) 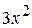 Б)
Б) 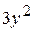 В)
В) 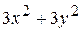 Г)
Г) 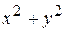
125. Частная производная 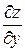 от функции
от функции 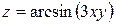 имеет вид:
имеет вид:
А) 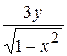 Б)
Б) 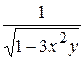 В)
В) 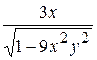 Г)
Г) 
126. Частная производная 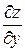 от функции
от функции 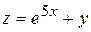 имеет вид:
имеет вид:
А) 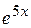 Б) 1 В)
Б) 1 В) 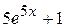 Г)
Г) 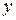
127. Частная производная 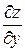 от функции
от функции 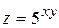 имеет вид:
имеет вид:
А) 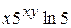 Б)
Б) 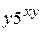 В)
В) 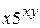 Г)
Г) 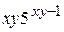
128. Градиент функции 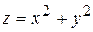 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (2;2) Б) (1;2) В) (2;1) Г) (1;1)
129. Градиент функции 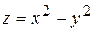 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (2; 2) Б) (2; -2) В) 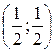 Г)
Г) 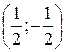
130. Градиент функции 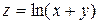 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (2; 2) Б) 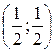 В)
В) 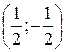 Г)
Г) 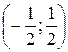
131. Градиент функции 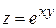 в точке М (1;0) равен:
в точке М (1;0) равен:
А) (0; 1) Б) (1; 0) В) (0; 0) Г) (1; 1)
132. Градиент функции 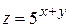 в точке М (0;1) равен:
в точке М (0;1) равен:
А) (0; 1) Б) (5ln5; 5ln5) В) (5; 0) Г) (0; 5)
133. Градиент функции 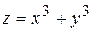 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (3; 3) Б) (3; 1) В) (1; 1) Г) 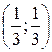
134. Градиент функции 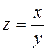 в точке М (2;3) равен:
в точке М (2;3) равен:
А) 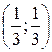 Б)
Б) 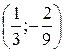 В)
В) 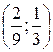 Г)
Г) 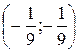
135. Градиент функции 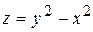 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (1; 1) Б) (-2; 2) В) (2; 2) Г) (2; -2)
136. Градиент функции 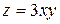 в точке М (-2;-2) равен:
в точке М (-2;-2) равен:
А) (-6; -6) Б) (3; 3) В) (6; 6) Г) (2; 2)
137. Градиент функции 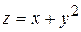 в точке М (1;1) равен:
в точке М (1;1) равен:
А) (1; 1) Б) (1; 2) В) (2; 2) Г) (2; 1)
138. Частная производная по х от функции 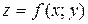 определяется равенством:
определяется равенством:
А) 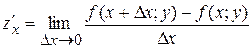
Б) 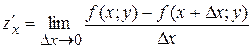
В) 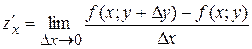
139. Частная производная по y от функции 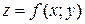 определяется равенством:
определяется равенством:
А) 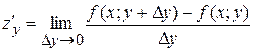
Б) 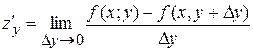
В) 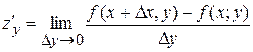
140. Формула для вычисления приближенных значений имеет вид:
А) 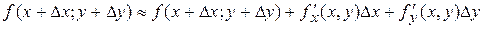
Б) 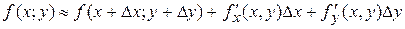
В) 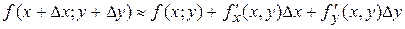
141. Точка (х0;у0) называется точкой максимумафункции 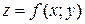 , если существует такая
, если существует такая 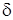 - окрестность точки (х0;у0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
- окрестность точки (х0;у0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
А) 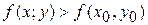
Б) 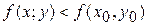
В) 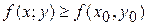
142. Точка (х0;у0) называется точкой минимумафункции 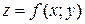 , если существует такая
, если существует такая 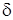 -окрестность точки (х0;у0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
-окрестность точки (х0;у0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
А) 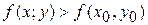
Б) 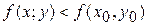
В) 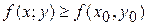
143. Если в точке N(х0;у0) дифференцируемая функция 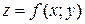 имеет экстремум, то ее частные производные в этой точке:
имеет экстремум, то ее частные производные в этой точке:
А) 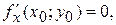
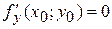
Б) 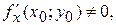
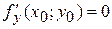
В) 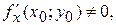
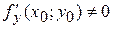
144. Производная по направлению 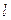 от функции
от функции 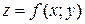 определяется равенством:
определяется равенством:
А) 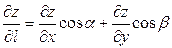
Б) 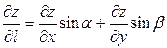
В) 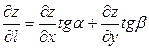
145. Градиентом функции 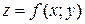 называется вектор с координатами:
называется вектор с координатами:
А) 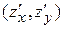
Б) 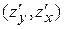
В) (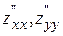 )
)
146. Функция Лагранжа имеет вид:
А) 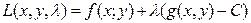
Б) 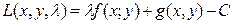
В) 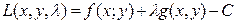
Дата добавления: 2015-10-30; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определенный интеграл | | | Неопределенный интеграл. |