
Читайте также:
|
ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В
СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
С ПОМОЩЬЮ ВЕЩЕСТВЕННЫХ ЧАСТОТНЫХ
ХАРАКТЕРИСТИК
Методические указания к выполнению лабораторной работы по дисциплине «Теория автоматического управления»
Севастополь
СОДЕРЖАНИЕ
Стр.
1 Цель работы 2
2 Краткие теоретические сведения 2
3 Описание технических средств выполнения работы 5
4 Порядок выполнения теоретических расчетов 5
5 Порядок выполнения экспериментальных исследований 5
6 Содержание отчета о выполнении лабораторной работы 6
7 Контрольные вопросы 6
Библиография 7
ЦЕЛЬ РАБОТЫ
Применение метода трапеций к исследованию переходных процессов в линейных системах автоматического управления (ЛСАУ).
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При решении различного рода задач управления всегда возникает необходимость исследования переходных процессов, протекающих в ЛСАУ.
Устойчивость является необходимым, но недостаточным условием работоспособности САУ. Устойчивость системы управления означает лишь то, что в системе происходит затухание переходного процесса под влиянием управляющего или возмущающего внешнего воздействия. Время затухания процесса, максимальное отклонение регулируемой величины и число колебаний в системе при этом не определяются, однако эти величины являются очень важными показателями качества процессов регулирования.
Показатели качества процессов регулирования можно определить с помощью различных методов. К числу их в первую очередь следует отнести построение переходных процессов по заданным передаточным функциям замкнутых систем [1]. Существует несколько методов построения переходных процессов в САУ [1,2], однако все они имеют свои определенные достоинства и недостатки, а также границы применимости.
В данной лабораторной работе решается задача построения переходного процесса в ЛСАУ методом трапецеидальных частотных характеристик [1,2]. 
Метод приближенного построения кривой переходного процесса в ЛСАУ по заданной вещественной частотной характеристике (ВЧХ) Р( замкнутой системы был разработан В.В. Солодовниковым в 1948 году. Этот способ полезен тогда, когда расчет системы ведется с самого начала частотными методами. Он совершенно необходим, если известны уравнения не всех звеньев системы, а часть из них задается экспериментально снятыми частотными характеристиками.
замкнутой системы был разработан В.В. Солодовниковым в 1948 году. Этот способ полезен тогда, когда расчет системы ведется с самого начала частотными методами. Он совершенно необходим, если известны уравнения не всех звеньев системы, а часть из них задается экспериментально снятыми частотными характеристиками.
Частотный метод построения переходных процессов заключается в графическом способе вычисления интеграла
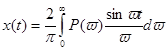 , t>0.
, t>0.
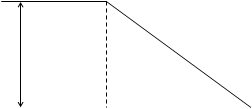
Представим кривую P  в виде суммы ряда типовых трапецеидальных кривых p
в виде суммы ряда типовых трапецеидальных кривых p 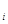 (
( (рис. 1):
(рис. 1): 

P(w) 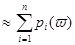 ; (1)
; (1)
тогда
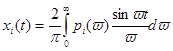 , (2)
, (2)
т.е.
 . (3)
. (3)

 |

0 

Рисунок 1 – Произвольная трапецеидальная частотная
характеристика
Будем считать, что функция  определяется с помощью следующего выражения:
определяется с помощью следующего выражения:
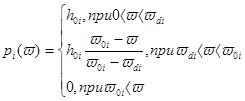 (4)
(4)
Функция  и представляет собой трапецеидальную частотную характеристику. Подставив выражение (4) в формулу (2), получим
и представляет собой трапецеидальную частотную характеристику. Подставив выражение (4) в формулу (2), получим
 (5)
(5)
откуда после ряда несложных преобразований найдем

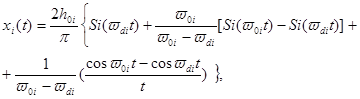 (6)
(6)
где
Si(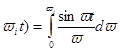 .
.
Для составления таблиц функции x  (t) В.В. Солодовников предложил использовать единичные трапецеидальные частотные характеристики, имеющие h
(t) В.В. Солодовников предложил использовать единичные трапецеидальные частотные характеристики, имеющие h 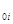 =1,
=1,  =1 и коэффициент c, изменяющийся в пределах от 0 до 1,0 (рис.2). Пользуясь этими характеристиками, переходную функцию в соответствии с формулой (6) можно представить в виде
=1 и коэффициент c, изменяющийся в пределах от 0 до 1,0 (рис.2). Пользуясь этими характеристиками, переходную функцию в соответствии с формулой (6) можно представить в виде
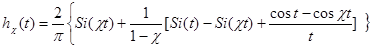 , (7)
, (7)
откуда видно, что функции h 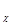 зависят только от одного параметра c, и их можно представить в виде таблиц. С помощью этих таблиц можно вычислять переходные процессы в системах регулирования с точностью 2-5%.
зависят только от одного параметра c, и их можно представить в виде таблиц. С помощью этих таблиц можно вычислять переходные процессы в системах регулирования с точностью 2-5%.
 p
p


 1
1

0 c 1 v[А1] [А2] [А3]
Рисунок 2 – Единичная трапецеидальная частотная
характеристика
Порядок построения переходного процесса по частотной характеристике замкнутой системы следующий:
1 Разбиваем ВЧХ на n трапеций. Определяем для каждой из трапеций 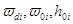 .
.
2 Вычисляем для каждой из трапеций наклон
 .
.
3 По вычисленному 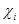 находим по таблице соответствующие значения
находим по таблице соответствующие значения 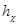 -функций при
-функций при 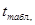
4 Полученные значения 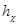 умножаем на высоты трапеций
умножаем на высоты трапеций 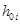 .
.
5 Откладывая по оси t значения t 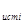 , а по оси ординат значения
, а по оси ординат значения 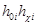 получим составляющие переходных процессов x
получим составляющие переходных процессов x 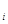 (t) для каждой из трапеций.
(t) для каждой из трапеций.
6 Складывая ординаты этих кривых с учетом их знака, получим искомый переходный процесс x(t).
3 ОПИСАНИЕ ТЕХНИЧЕСКИХ СРЕДСТВ ВЫПОЛНЕНИЯ РАБОТЫ
Построение ВЧХ и переходного процесса с помощью обратного преобразования Лапласа производится с использованием ПЭВМ и предлагаемых преподавателем пакетов прикладных программ.
4 ПОРЯДОК ВЫПОЛНЕНИЯ ТЕОРЕТИЧЕСКИХ РАСЧЕТОВ
В лабораторной работе исследуются замкнутые системы автоматического регулирования, заданные передаточной функцией вида
W(S)= 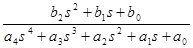
 (8)
(8)
Программа теоретических исследований:
а) Изучить метод трапеций.
б) Проанализировать устойчивость САУ с передаточной функцией (8).
Варианты исходных данных приведены в таблице 1.
в) По передаточной функции (8) получить выражение для построения ВЧХ замкнутой системы.
Пункты б и в теоретической части работы необходимо выполнить в форме предварительного отчета по лабораторной работе.
5 ПОРЯДОК ВЫПОЛНЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ
ИССЛЕДОВАНИЙ
а) Построить график ВЧХ.
б) Разбить построенную ВЧХ на требуемое число трапеций.
в) Построить переходный процесс в ЛСАУ методом трапеций.
г) Построить переходный процесс в ЛСАУ с помощью обратного преобразования Лапласа.
д) Сравнить переходные процессы, построенные методом трапеций и с помощью обратного преобразования Лапласа.
Графики ВЧХ и переходных процессов, построенные на экране монитора, распечатываются или зарисовываются и включаются в отчет по лабораторной работе.
6 СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ
РАБОТЫ
Отчет должен содержать:
а) Аналитическое исследование системы.
б) Результаты проведенных экспериментальных исследований в виде таблиц значений и графиков.
в) Краткие выводы.
Отчет по лабораторной работе должен быть выполнен в соответствии с требованиями ДСТУ.
Таблица 1 – Значения коэффициентов передаточной функции
замкнутой системы
| № вар. | b2 | b1 | b0 | a4 | a3 | a2 | a1 | a0 |
| 0.0035 | 0.370 | 9.50 | 0.000010 | 0.00103 | 0.02715 | 1.1225 | 1.315 | |
| 0.0037 | 0.372 | 9.52 | 0.000020 | 0.00105 | 0.02720 | 1.1230 | 1.316 | |
| 0.0039 | 0.374 | 9.52 | 0.000012 | 0.00107 | 0.02725 | 1.1235 | 1.317 | |
| 0.0041 | 0.376 | 9.56 | 0.000014 | 0.00109 | 0.02730 | 1.1240 | 1.318 | |
| 0.0042 | 0.378 | 9.58 | 0.000016 | 0.00111 | 0.02735 | 1.1245 | 1.319 | |
| 0.0044 | 0.380 | 9.60 | 0.000018 | 0.00113 | 0.02740 | 1.1250 | 1.320 | |
| 0.0046 | 0.382 | 9.62 | 0.000020 | 0.00115 | 0.02745 | 1.1255 | 1.321 | |
| 0.0048 | 0.384 | 9.64 | 0.000022 | 0.00117 | 0.02750 | 1.1260 | 1.322 | |
| 0.0053 | 0.386 | 9.66 | 0.000024 | 0.00119 | 0.02755 | 1.1265 | 1.323 | |
| 0.0057 | 0.388 | 9.68 | 0.000026 | 0.00121 | 0.02760 | 1.1270 | 1.324 | |
| 0.0060 | 0.390 | 9.70 | 0.000028 | 0.00123 | 0.02765 | 1.1275 | 1.325 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Дать определение частотной передаточной функции.
2 Как исследовать устойчивость и качество с помощью переходных процессов?
3 Какие существуют методы построения переходных процессов в ЛСАУ?
4 Дать сравнительный анализ алгебраического, частотного и численного методов расчета переходных процессов.
5 Поясните идею метода построения переходных процессов на основе частотных характеристик.
6 В чем заключается содержание метода трапеций?
БИБЛИОГРАФИЯ
1 Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1972.
2 Воронов А.А. Основы теории автоматического управления. Ч.I. – М.: Энергия, 1966.
3 Бесекерский В.А. и др. Сборник задач по теории автоматического регулирования и управления. – М.: Наука, 1978.
[А1]
[А2]
[А3]
Дата добавления: 2015-10-30; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| SAINT VS. SINNER | | | Схема и перечень обязанностей студента-куратора |