
Основные свойства неопределенного интеграла.
1)  . 2)
. 2)  . 3)
. 3)  .
.
4) 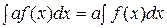 . 5)
. 5)  .
.
6.3. Таблица основных неопределённых интегралов.
1) 

. 

 9)
9)  .
.
2)  . 10)
. 10)  .
.
3) 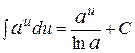 . 11)
. 11) 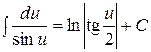 .
.
4)  . 12)
. 12)  .
.
5)  . 13)
. 13)  .
. 
6)  . 14)
. 14)  .
.
7)  . 15)
. 15)  .
.
8)  . 16)
. 16)  .
.
Основные методы интегрирования.
а) Метод непосредственного интегрирования.
Отыскание неопределенного интеграла с помощью таблицы 6.3 и тождественных преобразований называют непосредственным интегрированием.
Примеры. Непосредственным интегрированием найти следующие интегралы:
Ñ 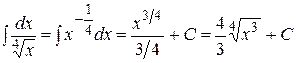 (формула 1 таблицы 6.3) #
(формула 1 таблицы 6.3) #
Ñ  (формула 3 таблицы 6.3) #
(формула 3 таблицы 6.3) #
Ñ  # (формула 15 из таблицы 6.3 и свойство 5 из 6.2)
# (формула 15 из таблицы 6.3 и свойство 5 из 6.2)
б)Метод подведения под знак дифференциала.
Напомним, что  , если
, если  . При интегрировании бывает удобно представить
. При интегрировании бывает удобно представить 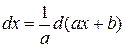 или
или  и.т.д. Это и используется при интегрировании методом подведения под знак дифференциала.
и.т.д. Это и используется при интегрировании методом подведения под знак дифференциала.
Примеры. Методом подведения под знак дифференциала найти следующие интегралы:
Ñ 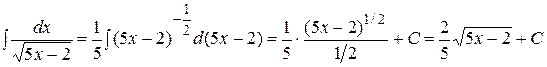 #
#
Ñ  #
#
Ñ  #
#
в) Метод замены переменной
Если подынтегральное выражение 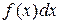 можно преобразовать к виду
можно преобразовать к виду 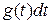 , где
, где  и
и 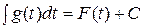 , то
, то 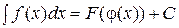 .
.
Примеры. Найти следующие интегралы методом замены переменной.
Ñ  . Сделаем подстановку
. Сделаем подстановку  .
.

 . #
. #
Ñ  . Заменим
. Заменим  .
.

г) Метод интегрирования по частям.
Если 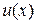 и
и  – непрерывно дифференцируемые функции, то имеет место формула:
– непрерывно дифференцируемые функции, то имеет место формула:  . (4.1.)
. (4.1.)
К  следует относить множители, которые упрощаются при дифференцировании. Формула (4.1) может применяться неоднократно. Интеграл, стоящий справа в (4.1) должен быть проще интеграла, стоящего слева.
следует относить множители, которые упрощаются при дифференцировании. Формула (4.1) может применяться неоднократно. Интеграл, стоящий справа в (4.1) должен быть проще интеграла, стоящего слева.
Примеры. Следующие интегралы найти интегрированием по частям:
Ñ 


 #
#
Ñ  =
=  #
#
Ñ 
= 
Получили уравнение относительно  . Решая его, будем иметь:
. Решая его, будем иметь:
 .
.
Интегралы такого типа называют циклическими.#
Задачи для самостоятельного решения
Найти интегралы методом непосредственного интегрирования.
1. 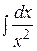 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12.
. 12.  .
.
Найти интегралы методом подведения под знак дифференциала.
13.  . 14.
. 14. 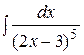 . 15.
. 15. 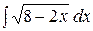 . 16.
. 16.  . 17.
. 17.  . 18.
. 18.  . 19.
. 19.  . 20.
. 20.  . 21.
. 21.  22.
22.  . 23.
. 23.  . 24.
. 24.  .
.
25. 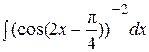 . 26.
. 26.  . 27.
. 27.  . 28.
. 28.  .
.
29. 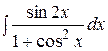 .30.
.30. 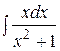 . 31.
. 31.  . 32.
. 32.  . 33.
. 33.  .
.
34.  . 35.
. 35.  . 36.
. 36. 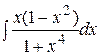 . 37.
. 37.  . 38.
. 38.  .
.
39.  . 40.
. 40.  .
.
Найти интегралы методом замены переменной.
41.  . 42.
. 42.  . 43.
. 43.  . 44.
. 44.  . 45.
. 45. 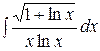 . 46.
. 46.  . 47.
. 47.  .
.
Найти интегралы методом интегрирования по частям.
48.  . 49.
. 49.  . 50.
. 50.  . 51.
. 51.  . 52.
. 52. 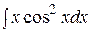 . 53.
. 53.  . 54.
. 54. 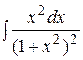 . 55.
. 55.  . 56.
. 56.  .
.
57.  . 58.
. 58.  . 59.
. 59.  . 60.
. 60. 
Интегрирование простейших функций, содержащих
квадратный трехчлен.
а) Интегралы вида  и
и  (5.1)
(5.1)
сводятся к табличным 13-16 после выделения из квадратного трехчлена полного квадрата.
Пример. Найти интеграл  .
.
Ñ 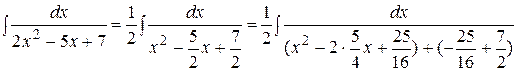 =
=
= 
=  . #
. #
б) Интегралы вида  и
и 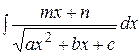 . (5.2)
. (5.2)
При интегрировании таких функций сначала в числителе создаётся дифференциал квадратного трехчлена:  . Числитель преобразуется следующим образом:
. Числитель преобразуется следующим образом:
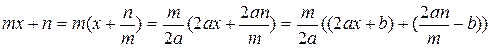 .
.
После этого данный интеграл по свойству 5 раздела 6.2. разбивается на два:  , первый из которых берётся по
, первый из которых берётся по
формуле 2 таблицы 6.3, а второй – интеграл (5.1), рассмотренный раньше. Аналогично берётся и второй интеграл из (5.2)
Пример. Найти интеграл 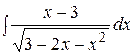 .
.
Ñ 

 .#
.#
в) Интегралы вида  . (5.3)
. (5.3)
Эти интегралы приводятся к интегралам (5.2) подстановкой 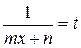 .
.
Пример. Найти интеграл  .
.
Ñ 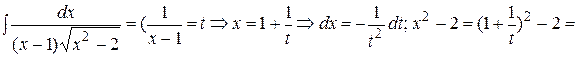


 . #
. #
Дата добавления: 2015-10-30; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| National organ and chamber music hall of Ukraine. | | | Области на плоскости |