
Читайте также:
|
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ОРЛОВСКАЯ БАНКОВСКАЯ ШКОЛА (КОЛЛЕДЖ) ЦЕНТРАЛЬНОГО БАНКА РОСИЙСКОЙ ФЕДЕРАЦИИ
РАБОЧАЯ ТЕТРАДЬ
ПО МАТЕМАТИКЕ
«ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ»
Студентки группы №___________________
__________________________________________
Рабочую тетрадь рекомендуется использовать в сочетании с учебным комплексом
под ред. Мордковича А.Г. «Алгебра и начала анализа»
ПРЕПОДАВАТЕЛЬ
Р.В.Пьянова
ПЕРВООБРАЗНАЯ
Теоретические вопросы.
1.Дайте определение первообразной функции.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практические задания по теме
1. Докажите, что функция 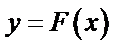 является первообразной для функции
является первообразной для функции 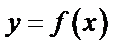 , если
, если 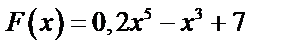 ,
, 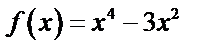
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Найдите первообразную для функции: 1) 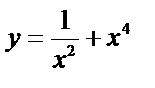 ; 2)
; 2) 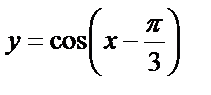 .
.
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3. Для функции 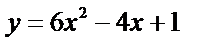 найдите ту первообразную, график которой проходит через точку
найдите ту первообразную, график которой проходит через точку 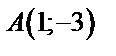 .
.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Творческая работа(это интересно знать)
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Теоретические вопросы.
1.Дайте определение неопределенного интеграла.
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практические задания по теме
| Найдите неопределенный интеграл | |||
1)  _______________________________________________________
__________________________________________________________________________
__________________________________________________________________________ _______________________________________________________
__________________________________________________________________________
__________________________________________________________________________
| |||
2) 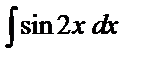 ________________________________________________________________
__________________________________________________________________________
3) ________________________________________________________________
__________________________________________________________________________
3)  -____________________________________________________________
__________________________________________________________________________ -____________________________________________________________
__________________________________________________________________________
| |||
4. 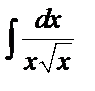 _________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________ _________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
| |||
5)  ______________________________________________
_________________________________________________________________________
_________________________________________________________________________
6) ______________________________________________
_________________________________________________________________________
_________________________________________________________________________
6) 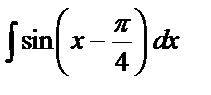 _________________________________________________________________________
__________________________________________________________________________
7)
_________________________________________________________________________
__________________________________________________________________________
7) 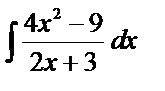 .___________________________________________________________
_________________________________________________________________________
__________________________________________________________________________ .___________________________________________________________
_________________________________________________________________________
__________________________________________________________________________
|
Творческая работа(это интересно знать)
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Теоретические вопросы.
1.Дайте определение определенного интеграла.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1. Какая фигура называется криволинейной трапецией?
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Как найти площадь криволинейной трапеции?
_________________________________________________________________________________
3. С помощью формулы Ньютона-Лейбница вычисляют:
А. Первообразную функции;
Б. Площадь криволинейной трапеции;
В. Интеграл;
Г. Производную.
Практические задания по теме
| 1.Найдите определенный интеграл | ||||
1) 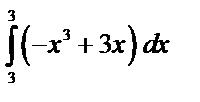 2)
2) 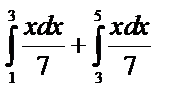
| ||||
3) 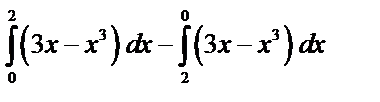 4)
4)  5)
5)  6)
6) 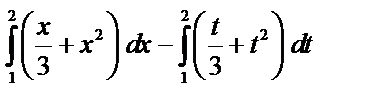 7)
7) 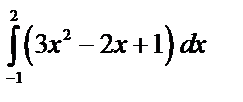 8)
8) 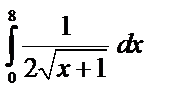 9)
9) 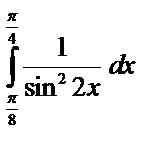 ;
10) ;
10) 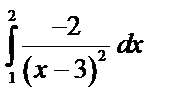
| ||||
| 3. Вычислите площадь фигуры, ограниченной линиями ПРИМЕР | |
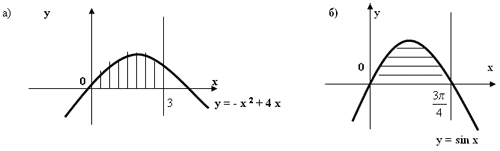 Решение:
Решение:
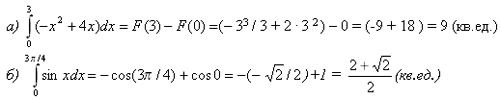 1)
1)  , ,  , , 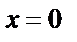 , ,  .
.
|
2). Какие из фигур являются криволинейными трапециями:
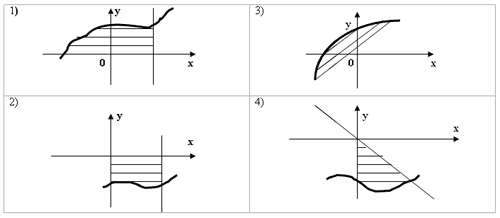
3). На каком рисунке изображена фигура, не являющаяся криволинейной трапецией?

4). Найдите площадь заштрихованной фигуры:

А. 0; Б. –2; В. 1; Г. 2.
5). Найдите площадь фигуры ограниченной осью Ох и параболой у = 9 – х2
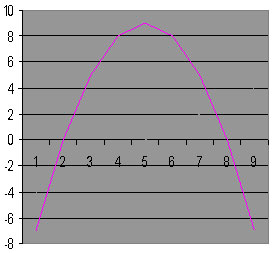
А. 18; Б. 36; В. 72; Г. Нельзя вычислить.
6). Найдите площадь фигуры, ограниченной графиком функции у = sin x, прямыми х = 0, х = 2 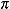 и осью абсцисс.
и осью абсцисс.
А. 0; Б. 2; В. 4; Г. Нельзя вычислить.
Творческая работа(это интересно знать)
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Учебно-тренировочные тестовые задания по теме «Первообразная и интеграл»
Тестовые задания базового уровня  .
.
| А1. Первообразная алгебраических функций | Ответы |
| А1.1 Найдите f (- 2), если f ¢(x) = 6x3 – 8x + 3, f (2) = 0. A) 10 B) 12 C) -12 D) 18 E) -18 | |
А1.2 Найдите первообразную функции 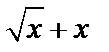 A)
A)  B) B)  C)
C)  D) D) 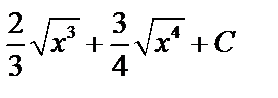 E)
E) 
| |
А1.3 Найдите все первообразные для функции 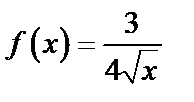 A) A)  + C B) 3 + C B) 3 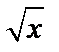 + C
C) + C
C) 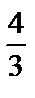 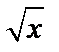 + C D) - + C D) - 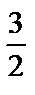 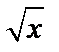 + C E) 6 + C E) 6 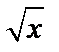 + C + C
| |
А1.4 Найдите первообразную функцию для  A) Y = (2x + 5)5 + C B) A) Y = (2x + 5)5 + C B) 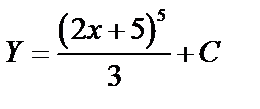 C)
C) 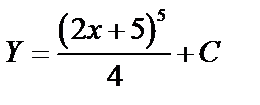 D) D)  E) Y = 4(2x + 5)3 + C
E) Y = 4(2x + 5)3 + C
| |
А1.5 Найдите первообразную функции f(x) = 8x3 – 5, график которой проходит через точку M(1; 4).
A) 2x4 – 5x + 7 B) 24x2 + 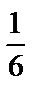 C) 2x4 – 5x
D) 2x4 – 5x + 1 E) 4x4 – 5x + 7 C) 2x4 – 5x
D) 2x4 – 5x + 1 E) 4x4 – 5x + 7
| |
| А1.6Найдите f(0), если f’(x)=6x2-3x+5 и f(4)=130. A) 6 B) 4 C) –4 D) –6 E) 8 | |
А1.7 Для функции  , найдите первообразную, график которой проходит через точку , найдите первообразную, график которой проходит через точку  . A) . A)  B) - B) - 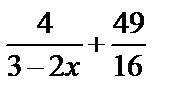 C) -
C) - 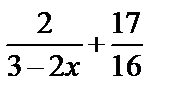 D) D) 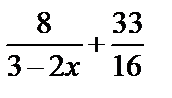 E) E) 
| |
А1.8 Найдите первообразную функции 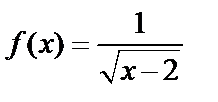 , график которой проходит через точку А(3; 5).
A) , график которой проходит через точку А(3; 5).
A) 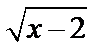 +4 B) 2 +4 B) 2 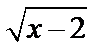 +3 C) +3 C) 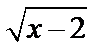 +3
D) 2 +3
D) 2 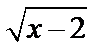 +4 E) +4 E) 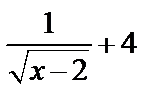
| |
| А2. Вычисление интегралов алгебраических функций | Ответы |
А2.1 Вычислите: 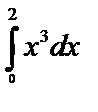 A) 4 B) -4 C) A) 4 B) -4 C)  D) 2 E) D) 2 E) 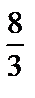
| |
А2.2 Вычислите: 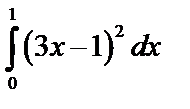 A) 3 B) 1 C) -
A) 3 B) 1 C) - 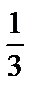 D) D)  E) 2 E) 2 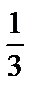
| |
А2.3 Вычислите:  A)
A) 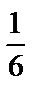 B) B) 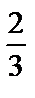 C) 1 D) C) 1 D) 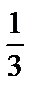 E) -1 E) -1
| |
А2.4Вычислите: 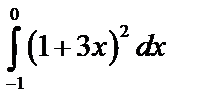 A) 1 B) -1 C)
A) 1 B) -1 C)  D) - D) - 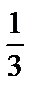 E) E) 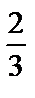
| |
А2.5 Вычислите  A) 45 B) 52 C) 54 D) 56 E) 6
A) 45 B) 52 C) 54 D) 56 E) 6
| |
А2.6 Вычислите 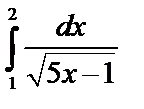 .
A) 1 B) .
A) 1 B)  C) C)  D) 2 E) D) 2 E) 
| |
А2.7 Вычислите  .
A) 18 B) 9 C) 27 D) 6 .
A) 18 B) 9 C) 27 D) 6 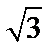 E) 9 E) 9 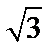
| |
А2.8 Вычислите  A) 7 B) 8 C) 10 D) 12 E) 15
A) 7 B) 8 C) 10 D) 12 E) 15
| |
| А3. Первообразная тригонометрических функций | Ответы |
А3.1 Для какой из следующих функций, функция
F(x) = 3tg x + 5 x + c является первообразной?
A)  B) B)  C) C) 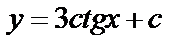 D)
D) 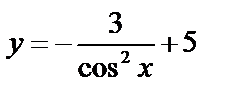 E) E) 
| |
А3.2Для какой из следующих функций функция
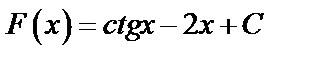 является первообразной?
A) является первообразной?
A) 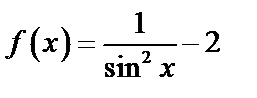 B) B) 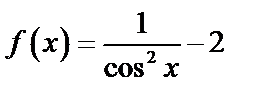 C)
C) 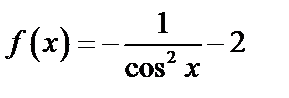 D) D) 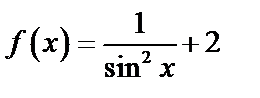 E)
E) 
| |
А3.3Укажите первообразную функции 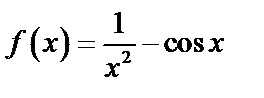 A)
A) 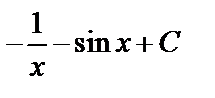 B) B) 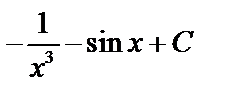 C) C) 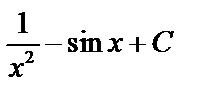 D) D) 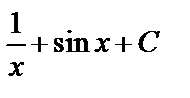
| |
А3.4Найдите первообразную функции: 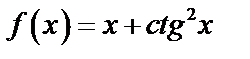 A)
A)  B) B)  C)
C) 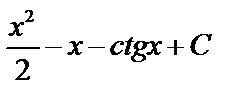 D) D) 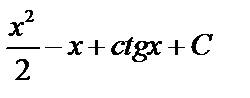 E) E) 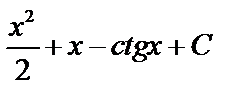
| |
А3.5Найдите первообразную для функции  . A) . A) 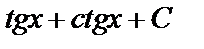 B) B)  C)
C)  D) D) 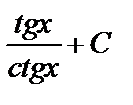 E) E) 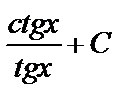
| |
А3.6 Укажите первообразную функции  A)
A) 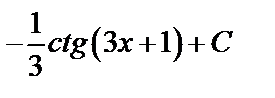 B) B) 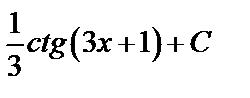 C)
C) 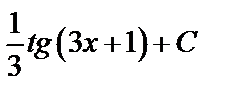 D) - D) - 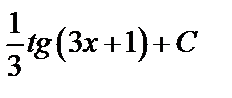 E) E) 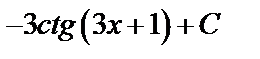
| |
А3.7Укажите первообразную функции: 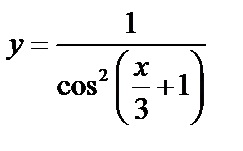 A)
A)  B) B) 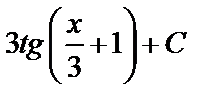 C) -
C) -  D) - D) - 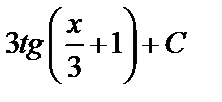 E) E) 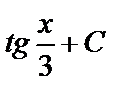
| |
А3.8Найдите первообразную функцию для функции
 = =  A) A)  B) ctg2x+ C
C) cos2x-sinx+ CD) B) ctg2x+ C
C) cos2x-sinx+ CD)  E) E) 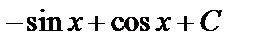
| |
| А4. Вычисление интегралов тригонометрических функций | Ответы |
А4.1 Вычислите  A)
A)  B) B)  C) 1 D) C) 1 D)  E) 2 E) 2
| |
А4.2Вычислите:  A) -
A) -  B) B)  C) C) 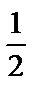 D) - D) - 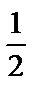 E) E) 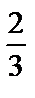
| |
А4.3Вычислите  A) -2 B) 1 C) -1 D) 2 E) 3
A) -2 B) 1 C) -1 D) 2 E) 3
| |
А4.4Вычислите 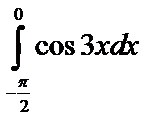 A)
A) 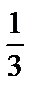 B) 0 C) - B) 0 C) - 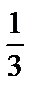 D) D) 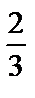 E) - E) - 
| |
А4.5Вычислите 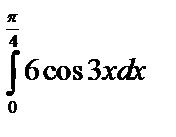 .
A) .
A) 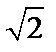 B) B)  C) 2 C) 2 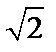 D) - D) - 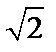 E) -2 E) -2 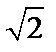
| |
А4.6 Вычислите: 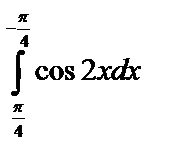 A) 0 B) -2 C) -1 D)
A) 0 B) -2 C) -1 D) 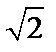 E) -2 E) -2 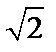
| |
А4.7Вычислите:  A)
A)  B) - B) -  C) 1 D) -1 E) 0 C) 1 D) -1 E) 0
| |
А4.8Вычислите 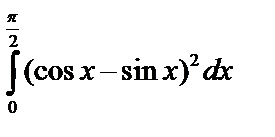 A)
A) 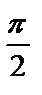 -1 B) 1 - -1 B) 1 - 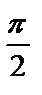 C) C) 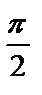 +1 D) p -1 E) 1 - p +1 D) p -1 E) 1 - p
| |
| А5. Площадь криволинейной трапеции | Ответы |
А5.1 Найдите площадь фигуры, ограниченной на отрезке 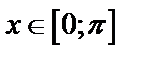 графиком функции графиком функции 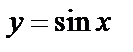 и осью абсцисс.
A) 1 B) 1,5 C) 2 D) 2,5 E) 3 и осью абсцисс.
A) 1 B) 1,5 C) 2 D) 2,5 E) 3
| |
А5.2Найдите площадь фигуры, ограниченной линиями
 , , 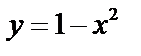 и x=0. A) и x=0. A) 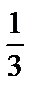 B) B)  C) C) 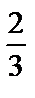 D) D)  E) 1 E) 1
| |
А5.3Найти площадь фигуры, ограниченной линиями:
y = 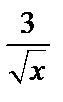 , y = 0, x = 1, x = 4. A 6 B 7 C 5 D 4 E 2 , y = 0, x = 1, x = 4. A 6 B 7 C 5 D 4 E 2
| |
А5.4Найдите площадь фигуры, ограниченной линиями
y = 4 –x2, y = -4x + 8 и осью  .
A) 1,5 B) 2 C) 2 .
A) 1,5 B) 2 C) 2 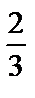 D) 3 E) 3 D) 3 E) 3 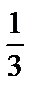
| |
А5.5Вычислить площадь фигуры, ограниченной линиями:
 , y = 0 и x = 4. A) 5 , y = 0 и x = 4. A) 5 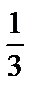 B) 5 B) 5 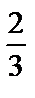 C) 5 D) 6 C) 5 D) 6  E)6 E)6 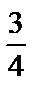
| |
А5.6 Найдите площадь фигуры, ограниченной линиями
y = 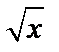 , y = x – 6 и y = 0.
A) 18,5 B) 36 C) 4,5 D) 18 E) 13,5 , y = x – 6 и y = 0.
A) 18,5 B) 36 C) 4,5 D) 18 E) 13,5
| |
| А5.7Вычислите площадь фигуры, ограниченной линиями y = 2x2, y = 0 и x = 3. A) 18 B) 27 C) 54 D) 36 E) 9 | |
А5.8Найти площадь фигуры, ограниченной линиями
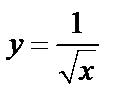 , y = 0, x = 1 и x = 4. A) 5 B) 2 C) 3 D) 1 E) 4 , y = 0, x = 1 и x = 4. A) 5 B) 2 C) 3 D) 1 E) 4
|
Тестовые задания более сложного уровня.
Дата добавления: 2015-10-30; просмотров: 88 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Task 3. Match the word combinations with their translation. | | | Интегрирование подстановкой |