Молекулярная физика. Министерство образования и науки Российской Федерации

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Колледж экономики, управления и права

Учебно- методическое пособие по учебной дисциплине

ФИЗИКА

Специальности

Информационные системы

Прикладная информатика

Ростов-на-Дону

Составитель (автор):

Джужук И.И.,

преподаватель колледжа

Рецензенты:

Учебно-методические пособие по физике разработано с учетом государственного образовательного стандарта среднего профессионального образования специальностей 230401.51 Информационные системы,230701.51 Прикладная информатика и предназначены для студентов и преподавателей колледжа.

Содержание

1. Программа по физике ………………………………………………………… 2. Краткие теоретические сведения ……………………………………………. 2.1. Кинематика …………………………………………………………......... 2.2. Динамика …………………………………………………………………. 2.3. Законы сохранения в механике. Механическая работа. Мощность. ……………………………………………………………….. 2.4. Жидкости и газы ………………………………………………………… 2.5. Молекулярная физика …………………………………………………... 2.6. Термодинамика ………………………………………………………….. 2.7. Электростатика ………………………………………………………….. 2.8. Постоянный электрический ток ……………………………………….. 2.9. Магнитное поле. Электромагнитная индукция. ……………………… 2.10. Механические колебания и волны …………………………………… 2.11. Электромагнитные колебания и волны ……………………………… 2.12. Геометрическая оптика ……………………………………………….. 2.13. Волновая оптика ………………………………………………………. 2.14. Основы специальной теории относительности ……………………… 2.15. Квантовая физика ……………………………………………………… 2.16. Физика атомного ядра ………………………………………………… 3. Задачи для самостоятельного решения ……………………………………. 3.1. Кинематика ……………………………………………………………… 3.2. Динамика ………………………………………………………………… 3.3. Жидкости и газы ………………………………………………………… 3.4. Законы сохранения в механике. Механическая работа. Мощность … 3.5. Молекулярная физика ………………………………………………….. 3.6. Термодинамика …………………………………………………………. 3.7. Электростатика …………………………………………………………. 3.8. Электрический ток ……………………………………………………… 3.9. Магнитное поле. Электромагнитная индукция ………………………. 3.10. Механические и электромагнитные колебания и волны …………… 3.11. Геометрическая оптика ……………………………………………….. 3.12. Волновая оптика ………………………………………………………. 3.13. Квантовая физика ……………………………………………………… 3.14. Физика атомного ядра ………………………………………………… 4. Задания для проверки знаний …..………………………………………….. 5. Табличные величины ………………………………………………………..

Программа по физике

Кинематика

1. Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение.

2. Скорость. Средняя и мгновенная скорость. Сложение скоростей.

3. Равномерное прямолинейное движение. Путь и скорость при равномерном прямолинейном движении.

4. Ускорение. Прямолинейное равноускоренное движение. Путь и скорость при прямолинейном равноускоренном движении.

5. Свободное падение тел. Ускорение свободного падения.

6. Криволинейное движение точки на примере движения по окружности с постоянной по модулю скоростью. Центростремительное ускорение.

Основы динамики

1. Инерция. Масса. Первый закон Ньютона. Инерциальная система отсчета. Принцип относительности Галилея.

2. Сила. Второй закон Ньютона. Принцип суперпозиции сил.

3. Третий закон Ньютона.

4. Сила тяготения. Закон всемирного тяготения. Сила тяжести.

5. Вес тела. Невесомость.

6. Первая космическая скорость.

7. Сила упругости. Закон Гука.

8. Сила трения. Коэффициент трения. Закон трения скольжения.

9. Момент силы. Условие равновесия твердого тела.

Законы сохранения в механике

1. Импульс тела. Закон сохранения импульса.

2. Механическая работа. Мощность.

3. Кинетическая энергия. Потенциальная энергия. Закон сохранения энергии в механике.

Жидкости и газы

1. Давление. Закон Паскаля для жидкостей и газов.

2. Сообщающиеся сосуды. Гидравлический пресс.

3. Архимедова сила для жидкостей и газов. Условия плавания тел.

Молекулярная физика

1. Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Диффузия. Взаимодействие молекул.

2. Масса и размер молекул..Количество вещества. Постоянная Авогадро.

3. Модель идеального газа. Основное уравнение молекулярно-кинетической теории идеального газа. Связь абсолютной температуры со средней кинетической энергией молекул идеального газа. Среднеквадратическая скорость молекул идеального газа.

4. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа). Универсальная газовая постоянная.

5. Изотермический, изохорный и изобарный процессы в идеальных газах.

6. Закон Дальтона.

Основы термодинамики

1. Внутренняя энергия. Количество теплоты. Теплоемкость вещества.

2. Работа в термодинамике. Первый закон термодинамики (закон сохранения энергии в тепловых процессах).

3. Испарение и конденсация. Кипение жидкости.

4. Преобразование энергии при изменениях агрегатного состояния вещества.

5. Применение первого закона термодинамики к изопроцессам в идеальных газах.

6. Адиабатный процесс.

7. Преобразование энергии в тепловых двигателях. КПД теплового двигателя.

8. Насыщенные и ненасыщенные пары.

9. Абсолютная и относительная влажность воздуха.

Электростатика

1. Электрический заряд. Элементарный электрический заряд. Закон сохранения электрического заряда. Взаимодействие заряженных тел. Закон Кулона

2. Электрическое поле. Напряженность электрического поля. Электрическое поле точечного заряда.

3. Потенциал электростатического поля. Разность потенциалов. Принцип суперпозиции полей.

4. Работа сил электрического поля при перемещении заряда.

5. Диэлектрики в электрическом поле. Диэлектрическая проницаемость.

6. Проводники в электрическом поле. Электрическая емкость.

7. Конденсатор. Емкость плоского конденсатора. Емкость сферического конденсатора.

8. Энергия электрического поля конденсатора.

9. Соединения конденсаторов.

Постоянный электрический ток.

1. Электрический ток. Сила тока. Напряжение.

2. Закон Ома для участка цепи. Сопротивление проводников.

3. Последовательное и параллельное соединение проводников.

4. Электродвижущая сила. Закон Ома для полной цепи.

5. Работа и мощность тока. Закон Джоуля-Ленца.

Магнитное поле. Электромагнитная индукция.

1. Магнитное поле. Индукция магнитного поля.

2. Действие магнитного поля на проводник с током. Сила Ампера.

3. Действие магнитного поля на электрические заряды. Сила Лоренца.

4. Магнитный поток. Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Правило Ленца.

5. Самоиндукция. Индуктивность. Энергия магнитного поля контура с током.

Механические колебания и волны

1. Гармонические колебания. Амплитуда, период и частота колебаний. Максимальные значения скорости и ускорения при гармонических колебаниях.

2. Превращение энергии при гармонических колебаниях.

3. Математический маятник. Период колебаний математического маятника.

4. Пружинный маятник. Период колебаний пружинного маятника.

5. Вынужденные колебания. Резонанс.

6. Механические волны. Поперечные и продольные волны.

7. Скорость распространения волн. Длина волны. Связь длины волны со скоростью ее распространения.

Электромагнитные колебания и волны

1. Колебательный контур. Свободные электромагнитные колебания в контуре. Период и частота свободных колебаний в контуре.

2. Превращение энергии в колебательном контуре.

3. Вынужденные электрические колебания. Резонанс в электрической цепи.

4. Переменный электрический ток.

5. Электромагнитные волны. Скорость распространения электромагнитных волн. Свойства электромагнитных волн.

Геометрическая оптика

1. Прямолинейное распространение, отражение и преломление света. Луч. Скорость света. Абсолютный показатель преломления. Относительный показатель преломления.

2. Законы отражения и преломления света. Полное отражение. Предельный угол полного отражения.

3. Построение изображений в плоском зеркале.

4. Линзы. Формула тонкой линзы. Построение изображения в линзе.

Волновая оптика

1. Свет – электромагнитная волна. Когерентность. Интерференция света.

2. Дифракция света. Дифракционная решетка.

3. Дисперсия света.

4. Поперечность световых волн. Поляризация света.

Основы специальной теории относительности

1. Инвариантность скорости света. Принцип относительности Эйнштейна.

2. Пространство и время в специальной теории относительности.

3. Связь массы и энергии.

Квантовая и ядерная физика

1. Тепловое излучение. Формула Планка. Постоянная Планка.

2. Внешний фотоэффект. Уравнение Эйнштейна для фотоэффекта.

3. Планетарная модель атома.

4. Боровская модель атома водорода.

5. Нуклонная модель ядра. Заряд ядра. Массовое число ядра.

6. Ядерные реакции. Сохранение заряда и массового числа при ядерных реакциях.

7. Энергия связи частиц в ядре. Деление ядер. Синтез ядер. Выделение энергии при делении и синтезе ядер.

8. Радиоактивность. Альфа-, бета-, гамма-излучения. Закон радиоактивного распада.

Краткие теоретические сведения

Кинематика

Кинематика изучает механическое движение тел, не рассматривая причины, вызывающие это движение.

Механические движение — изменение положения данного тела относительно другого тела или частей тела относительно других частей этого же тела, происходящее с течением времени.

Тело отсчета — тело, относительно которого рассматривается данное механическое движение.

Система отсчета — это система координат, связанная с телом отсчета и снабженная часами.

Материальная точка — тело, размерами которого в данной задаче можно пренебречь.

Траектория — линия, которую описывает материальная точка при своем движении.

Поступательное движение — движение, при котором все точки тела движутся по одинаковым траекториям. В этом случае тело можно считать материальной точкой.

Путь S (м) — расстояние, пройденное телом вдоль траектории движения. Путь — скалярная величина.

Перемещение 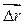(м) — вектор, соединяющий начальное и конечное положения материальной точки. Модуль перемещения ï 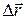ï — скалярная величина, равная длине этого вектора.

Относительность движения состоит в том, что траектория движения, путь и перемещение зависят от выбора системы отсчета. Следовательно, любое механическое движение относительно.

Скорость — физическая величина, характеризующая быстроту изменения положения тела в пространстве с течением времени.

Средняя скорость перемещения (движения) 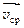(м/с) — вектор, равный отношению перемещения материальной точки 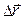к времени перемещения D t:

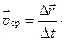
Средняя скорость перемещения направлена вдоль перемещения.

Мгновенная скорость — скорость тела в данный момент времени. Мгновенная скорость 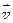равна пределу средней скорости перемещения при неограниченном уменьшении промежутка времени D t. Мгновенная скорость направлена по касательной к траектории движения материальной точки.

Средняя путевая скорость v _ср (м/с) равна отношению пути D S к времени движения D t:

.

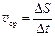Закон сложения скоростей. Если тело одновременно участвует в двух движениях со скоростям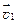и и 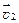, то его результирующая скорость определяется по правилу сложения векторов:

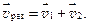
Относительная скорость. Если два тела движутся со скоростям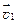и и 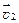относительно некоторой системы отсчета, то скорость 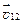первого тела относительно второго тела равна:

.

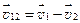Прямолинейное равномерное движение — движение, при котором тело движется вдоль прямой линии с постоянной по величине скоростью.

Путь при прямолинейном равномерном движении прямо пропорционален времени движения (рис. 1):

S = vt.

Уравнение прямолинейного равномерного движения:

X = X ₀ + v_x t,

где: X – координата тела, X ₀ – начальная координата, v_x – проекция скорости.

v, м/с

Х, м

Графическое представление прямолинейного равномерного движения

Х 0 t, с	t, с	t, с
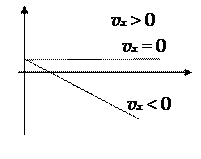
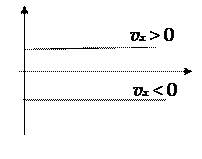
Зависимость пройденного пути от времени	Зависимость координаты от времени	Зависимость скорости от времени
Рис. 1

Ускорение 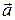(м/с²) — величина, равная отношению изменения скорости ко времени этого изменения:

.

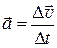Ускорение характеризует быстроту изменения скорости с течением времени.

Прямолинейное равноускоренное движение — движение тела по прямой линии с постоянным ускорением (рис 2).

Уравнение прямолинейного равноускоренного движения:

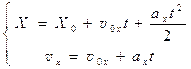
где a_x (м/с²), v _{0 x} (м/с), v_x (м/с) — проекции ускорения, начальной и конечной скорости движения.

Если при прямолинейном равноускоренном движении тела направление вектора скорости остается постоянным удобно использовать блок формул:

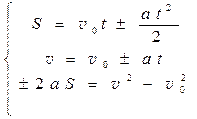
“+” ¾ при ускоренном движении,

“–” ¾ при замедленном движении.

Графическое представление прямолинейного равноускоренного движения

v t, с	t, с
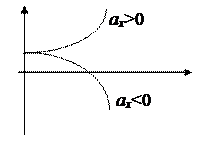
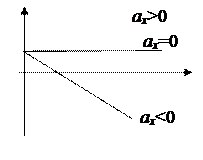
Зависимость координаты от времени	Зависимость скорости от времени
Рис. 2

Движение тела под действием только силы тяжести называется свободным падением.

При свободном падении возле поверхности Земли тело движется с ускорением g = 9,8 м/с². Если нет специальных оговорок, ускорение свободного падения можно принять равным g» 10 м/с².

Криволинейное движение — это движение тела по криволинейной траектории. При криволинейном движении вектор скорости меняет свое направление. Частным случаем криволинейного движения является движение материальной точки по окружности.

Период Т, (с) – время одного полного оборота тела.

Частота n, (Гц) – количество оборотов в единицу времени.

Угловая скорость w, (рад/с) — быстрота изменения угла поворота.

При равномерном движении по окружности радиуса R с постоянной по величине скоростью 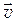материальная точка обладает центростремительным ускорением 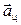, характеризующим, быстроту изменения направления вектора скорости 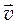. Вектор 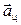направлен по радиусу к центру окружности (рис. 3).

	Рис. 3

Движение тела по окружности с постоянной по модулю скоростью можно описать следующим блоком формул:

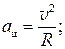
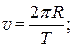
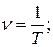
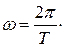
Динамика

Динамика изучает причины, вызывающие механическое движение.

Инерцией или инертностью называется способность тела сохранять состояние покоя или прямолинейного равномерного движения, если на это тело не действуют другие тела.

Первый закон Ньютона.

Существуют такие системы отсчета, в которых тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют другие тела.

Системы отсчета, для которых выполняется первый закон Ньютона, называются инерциальными.

Масса m, (кг) – мера инертных и гравитационных свойств тела.

Плотность r, (кг/м3) — отношение массы m тела к его объему V:

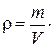
Сила 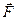(Н) — векторная величина, характеризующая взаимодействие между телами или частями тела.

Если на материальную точку действуют одновременно силы 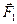и 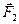, то их можно заменить результирующей силой :

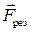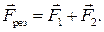
Второй закон Ньютона.

Ускорение, приобретаемое телом, прямо пропорционально результирующей сил и обратно пропорционально его массе.

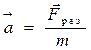
Направление ускорения 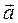совпадает с направлением .

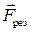При решении задач 2-й закон Ньютона удобнее записывать в следующем виде:

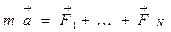
где N — количество сил, действующих на тело.

Третий закон Ньютона.

Силы взаимодействия двух материальных точек равны по величине и направлены в противоположные стороны вдоль прямой, соединяющей эти точки:

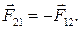
Эти силы приложены к разным телам, поэтому не компенсируют друг друга.

Сила тяготения — это сила притяжения, существующая между любыми материальными телами.

Закон всемирного тяготения.

Сила притяжения F двух материальных точек прямо пропорциональна массам m ₁и m ₂этих точек и обратно пропорциональна квадрату расстояния r между ними:

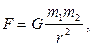
G = 6,67×10^-11Н×м²/кг² — гравитационная постоянная.

Закон всемирного тяготения выполняется также для двух однородных шаров, если за расстояние r принять расстояние между центрами шаров.

Сила тяжести 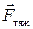— сила, действующая на тело вследствие его притяжения к Земле или другим небесным телам.

Вблизи поверхности Земли тело массой m под действием силы тяжести 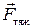движется с ускорением свободного падения 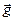. Поэтому по второму закону Ньютона сила тяжести равна:

.

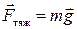При движения по круговой орбите вокруг планеты тело имеет центростремительное ускорение, равное ускорению свободного падения (р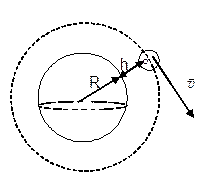ис. 4).

Рис. 4

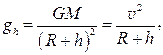где M ¾ масса планеты, R ¾ радиус планеты, h ¾ высота над поверхностью планеты, v – первая космическая скорость (минимальная скорость, которую нужно сообщить телу, чтобы оно превратилось в искусственный спутник планеты).

Первая космическая скорость для любой планеты рассчитывается по формуле:

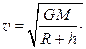
Вес тела 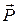— сила, с которой тело действует на опору или подвес вследствие действия на это тело силы тяжести. Вес тела приложен к опоре или подвесу.

Если скорость опоры или подвеса постоянна, то вес тела равен силе тяжести:

=

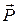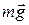
Если тело движется с ускорением, направленным вверх, то вес тела увеличивается. Если ускорение тела направлено вниз — вес тела уменьшается.

Р = m (g ± a)

“+” — если ускорение тела направлено вверх, “–” — если ускорение тела направлено вниз.

Невесомость — отсутствие веса, то есть в этом случае тело не действует на опору или подвес.

Перегрузка равна отношению веса тела к действующей на тело силе тяжести:

К = P / (m×g)

Деформацией называется изменение формы или размеров тела. Деформация является упругой, если тело восстанавливает первоначальную форму или размеры после устранения причин деформации.

Сила упругости возникает при упругих деформациях и стремится вернуть телу первоначальную форму или размеры.

Закон Гука.

Сила упругости F _упр. , возникающая в деформированной пружине, пропорциональна изменению длины пружины D Х:

F _упр. = - k ×D Х,

где k (Н/м) — коэффициент упругости или жесткость пружины.

Знак «–» означает, что сила упругости направлена против изменения длины пружины.

При решении задач можно использовать формулу для модуля силы упругости: F _упр. = k ×D Х

Сила реакции опоры 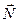— это сила, действующая на тело со стороны опоры перпендикулярно поверхности тела.

Силы трения возникают между поверхностями соприкасающихся тел и направлены против их относительного перемещения.

Закон трения скольжения.

Величина силы трения скольжения F _тр. прямо пропорциональна силе реакции опоры N:

F _{тр. =} m N,

где m — коэффициент трения скольжения, зависящий от материала тел и качества обработки их поверхностей.

Плечо силы l (м) — кратчайшее расстояние от оси вращения тела до линии действия силы.

Момент силы М (Н×м) — произведение силы на ее плечо.

M = Fl

Момент силы будем считать положительным, если сила вращает тело против направления вращения часовой стрелки, отрицательным — по направлению вращения часовой стрелки.

Тело находится в равновесии, если выполняются условия: 1) Векторная сумма внешних сил равна нулю. 2) Сумма моментов сил равна нулю.

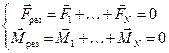
2.3. З аконы сохранения в механике. Механическая работа. Мощность.

Импульс тела 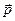(кг×м/c) — векторная величина, равная произведению массы тела m на его скорость :

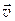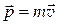
Если система состоит из N тел, то полный импульс этой системы 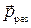равен векторной сумме импульсов всех тел:

_.

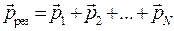Система тел называется замкнутой, если на нее не действуют внешние силы.

Закон сохранения импульса.

Полный импульс замкнутой системы есть величина постоянная:

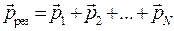= const

или

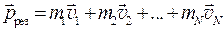. = const.

Импульс тела связан с силой соотношением:

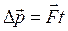
Механическая работа А (Дж) — скалярная величина, равная

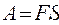cos a,

где F — величина силы, действующей на тело; S — величина перемещения тела; a — угол между векторами силы и перемещения.

а) если a = 0, то cos a = 1 Þ А > 0;

б) если a = 180°, то cos a = -1 Þ А < 0;

в) если a = 90°, то cos a = 0 Þ А = 0.

Мощность N (Вт) — это работа, совершаемая в единицу времени:

.

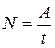Связь между мощностью N, силой F и скоростью тела v:

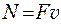cos a,

где a — угол между векторами силы и скорости.

Энергия — это способность тела совершать работу.

Существует два вида механической энергии: кинетическая энергия и потенциальная энергия.

Кинетическая энергия Е _к (Дж) — это энергия тела массой m, движущегося со скоростью v:

.

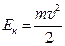Теорема об изменении кинетической энергии.

Изменение кинетической энергии тела равно работе A всех сил, действующих на это тело:

D E_к = Е_к2 – Е_к1 = А.

Потенциальная энергия Е_п (Дж) — энергия взаимодействия тел или частей тела, обусловленная их взаимным расположением.

Примеры:

а) Потенциальная энергия тела массой m, находящегося на высоте h, равна работе силы тяжести:

Е_п = mgh,

где g — ускорение свободного падения.

б) Потенциальная энергия пружины, деформированной на величину D Х, равна работе, которую совершает сила упругости при возвращении пружины в положение равновесия:

Е_п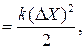

где k - коэффициент упругости (жесткость) пружины.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения тела.

Примеры: сила тяжести, сила упругости.

Система тел называется консервативной, если в ней действуют только потенциальные силы.

Закон сохранения энергии в механике.

Полная механическая энергия E консервативной системы тел сохраняется:

Е = Е_к + Е_п = const.

Абсолютно неупругим называется удар (взаимодействие), в результате которого взаимодействующие тела движутся как единое целое. В этом случае закон сохранения полного импульса системы выполняется, а механическая энергия не сохраняется.

Жидкости и газы

Давление p (Па) — скалярная величина, равная отношению силы нормального давления F к площади S поверхности, на которую действует эта сила:

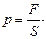
Закон Паскаля.

В данной точке жидкости или газа давление одинаково по всем направлениям:

p_x = р_y = р_z = const.

Давление p столба жидкости высотой h на дно сосуда:

,

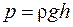где r — плотность жидкости; g — ускорение свободного падения.

Сообщающиеся сосуды — сосуды, соединенные между собой так, что жидкость может свободно перетекать из одного сосуда в другой.

Жидкости в сообщающихся сосудах находятся в равновесии при условии равенства их давлений:

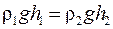
Высоты столбов разнородных жидкостей в сообщающихся сосудах обратно пропорциональны плотностям этих жидкостей.

,

где h ₁, h ₂ - высоты столбов, r₁, r₂ – плотности жидкостей.

Если жидкость однородна, то r₁ = r₂ и, следовательно, h ₁ = h ₂.

Гидравлический пресс.

Устройство, работающее по принципу сообщающихся сосудов и служащее для увеличения силы (рис. 5).

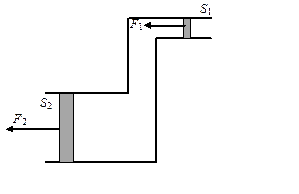
Рис. 5

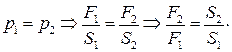
Закон Архимеда

На тело, погруженное в жидкость (газ), действует выталкивающая (архимедова) сила F_A, численно равная весу жидкости (газа), содержащейся в объеме погруженной части тела, и направленная вертикально вверх:

,

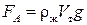где r_ж — плотность жидкости (газа), V _т — объем погруженной части тела, g — ускорение свободного падения.

Условия плавания тел:

а) если F_A < mg — тело тонет,

б) если F_A = mg — тело плавает в жидкости,

в) если F_A > mg — тело всплывает.

Молекулярная физика

Молекулярно-кинетическая теория (МКТ) объясняет строение и свойства тела движением и взаимодействием атомов или молекул тела.

Основные положения МКТ:

1) Все тела состоят из частиц – атомов или молекул.

2) Эти частицы движутся непрерывно и хаотически.

3) Частицы любого вещества взаимодействуют между собой - притягиваются или отталкиваются.

Опытные обоснования основных положений МКТ:

а) броуновское движение — непрерывное хаотическое движение взвешенных в жидкости частиц, обусловленное ударами молекул жидкости;

б) диффузия — взаимное проникновение молекул одних веществ между молекулами других;

в) проявление сил упругости в газах, жидкостях и твердых телах.

Мерой количества частиц в теле является количество вещества n (моль).

Постоянная Авогадро N _A – число молекул, содержащихся в одном моле любого вещества:

N _A = 6,02× 10²³ моль^-1.

Количество частиц определяется выражением:

N = N _A n

Молярная масса m— это масса одного моля вещества:

m = m /n, [m] – кг/моль,

где m - масса вещества, n — число молей.

Массу m₀ молекулы можно определить по формуле:

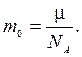
Модель идеального газа

Идеальный газ — модель газа, в которой:

1) молекулы газа не взаимодействуют между собой на расстоянии;

2) при соударении друг с другом и со стенками сосуда молекулы ведут себя подобно упругим шарам;

3) объемом молекул можно пренебречь по сравнению с объемом газа.

При комнатной температуре и нормальном давлении большинство газов можно считать идеальными.

Основное уравнение молекулярно-кинетической теории связывает микроскопические и макроскопические параметры идеального газа:

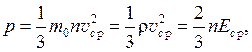
где р — давление газа; m ₀ - масса одной частицы; n = N / V (м^-3) — концентрация частиц; r(кг/м³) — плотность газа, v _ср(м/с) — среднеквадратичная скорость движения частиц, Е _ср (Дж) — средняя кинетическая энергия одной частицы.

Абсолютная температура Т (K) является мерой кинетической энергии хаотического поступательного движения молекул вещества.

T (К) = t °C + 273 К,

где t °С — температура по шкале Цельсия.

Средняя кинетическая энергия Е _cp (Дж) поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:

,

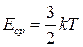где 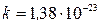Дж/К — постоянная Больцмана.

Среднеквадратичная скорость поступательного движения молекул идеального газа:

,

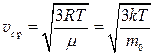где R = 8,31 Дж/(моль×К)— универсальная газовая постоянная, Т — абсолютная температура, m — молярная масса газа, k — постоянная Больцмана, m ₀ — масса молекулы.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа):

,

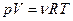где p - давление, V - объем, n- количество вещества, R — универсальная газовая постоянная, T – абсолютная температура.

Так же это уравнение можно записать в виде:

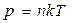
Если количество газа постоянна (n = const) газовый процесс описывается уравнением Клапейрона:

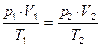
где 1 — начальные параметры газа; 2 — конечные параметры газа.

Изопроцессы в идеальном газе:

Если n = const и T = const — изотермический процесс.

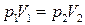— закон Бойля – Мариотта (рис. 6).

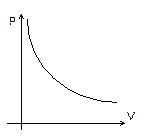
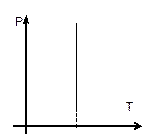
Рис. 6

Если n = const и V = const — изохорный процесс.

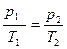— закон Шарля (рис. 7).

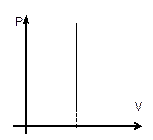
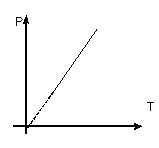
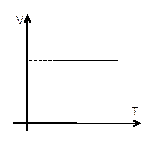
Рис. 7

Если n = const и p = const — изобарный процесс.

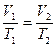— закон Гей-Люссака (рис. 8).

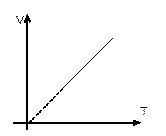
Рис. 8

Закон Дальтона.

Давление смеси газов равно сумме парциальных давлений каждого газа.

р _об = р ₁ + р ₂ + …+ р _n.

Парциальное давление газа — давление данного газа в объеме, занимаемом смесью газов.

Термодинамика

Внутренняя энергия вещества – это энергия атомов и молекул данного вещества.

Внутренняя энергия U (Дж) идеального газа равна кинетической энергии всех его молекул.

Для идеального одноатомного газа внутренняя энергия равна:

,

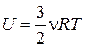где n — число молей газа, R — универсальная газовая постоянная, Т — абсолютная температура.

Изменение внутренней энергии идеального одноатомного газа равно:

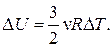
Одноатомными идеальными газами являются все инертные газы (гелий, аргон, неон).

Газ совершает работу при изменении его объема.

Работа газа определяется по формуле:

,

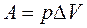где р — давление газа, D V — изменение объема газа.

Работа газа численно равна площади фигуры, ограниченной графиком p = f (V).

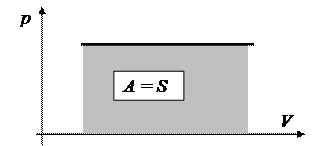
Рис. 9

Количество теплоты Q (Дж) — это мера энергии, передаваемой системе в процессе теплообмена, т. е. без совершения механической работы.

1. Нагревание (охлаждение) тела.

Количество теплоты, поглощаемое телом при нагревании (выделяемое при охлаждении) определяется по формуле:

,

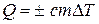с — удельная теплоемкость вещества, Дж/кг×К;

С = сm — теплоемкость тела, Дж/К.

Знак «+» ставят при нагревании, «–» — при охлаждении тела.

2. Плавление (кристаллизация) вещества.

Количество теплоты, поглощаемое в процессе плавления (выделяемое в процессе кристаллизации) определяется по формуле:

,

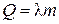l — удельная теплота плавления вещества, Дж/кг.

Плавление и кристаллизация происходят при постоянной для каждого вещества температуре — температуре плавления.

3. Испарение (конденсация) вещества.

Количество теплоты, поглощаемое в процессе испарения (выделяемое в процессе конденсации) определяется по формуле:

,

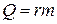r — удельная теплота парообразования, Дж/кг.

Кипение происходит при постоянной для каждого вещества температуре кипения, зависящей от внешнего давления.

4. Горение топлива.

Количество теплоты, выделяющееся при сгорании топлива, определяется по формуле:

,

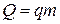q — удельная теплота сгорания топлива, Дж/кг.

Уравнение теплового баланса: количество теплоты, которое выделяют тела равно количеству теплоты, которое поглощается другими телами с учетом тепловых потерь (рис 10).

Q _выдел h = Q _погл

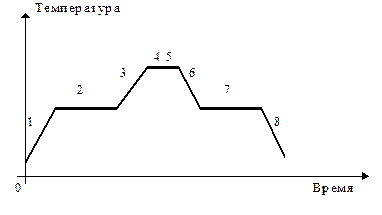
Рис. 10

1 – нагревание твердого тела, 2 – плавление, 3 – нагревание жидкости, 4 – кипение, 5 – конденсация, 6 – охлаждение жидкости, 7 – кристаллизация, 8 – охлаждение твердого тела.

Закон сохранения энергии в тепловых процессах (первый закон термодинамики).

Количество теплоты Q, сообщенное системе (газу), идет на изменение внутренней энергии D U системы и на работу А, совершаемую системой против внешних сил:

Q = D U + A.

Применение первого закона термодинамики к изопроцессам в идеальных газах.

1) Изотермический процесс.

Температура в этом процессе постоянна T = const, поэтому изменение температуры D T = 0. Следовательно, изменение внутренней энергии: D U = 0.

Первый закон термодинамики для изотермического процесса:

Q = A.

2) Изохорный процесс.

Так как в этом процессе объем V = const, то изменение объема D V = 0и, следовательно, работа газа A = p D V = 0.

Первый закон термодинамики для изохорного процесса:

Q = D U.

3) Изобарный процесс.

Так как здесь давление не изменяется (p = const),то из уравнения Менделеева – Клапейрона следует, что работа газа

A= pDV = n RDT,

где D V - изменение объема, n- число молей, D T - изменение температуры газа, R - универсальная газовая постоянная.

Первый закон термодинамики для изобарного процесса:

Q = D U + А.

Адиабатный процесс — процесс, протекающий без теплообмена с окружающей средой:

Q = 0.

Первый закон термодинамики для адиабатного процесса:

A = – DU,

то есть газ совершает работу А только за счет уменьшения своей внутренней энергии D U.

Тепловой двигатель — устройство для преобразования внутренней энергии топлива в механическую работу.

Коэффициент полезного действия (КПД) hтеплового двигателя - это отношение полезной работы А к количеству тепла Q _н, полученного двигателем от нагревателя (рис. 11):

Рис. 11

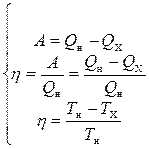
A — работа газа; Q _н — количество теплоты, полученное двигателем от нагревателя; Q _х — количество теплоты, переданное двигателем холодильнику; Т _н — температура нагревателя; Т _х — температура холодильника; h — коэффициент полезного действия (КПД).

Пар называется ненасыщенным, если количество испаряющихся молекул больше количества молекул перешедших в жидкость в результате конденсации.

Пар называется насыщенным, если он находится в состоянии термодинамического равновесия с жидкостью, т.е. количество испарившихся молекул равно количеству молекул перешедших в жидкость. Давление и плотность насыщенного пара зависят от его температуры.

Абсолютная влажность ¾ плотность водяного пара в атмосфере

.

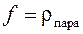Относительная влажность воздуха равна отношению плотности водяных паров в атмосфере к плотности насыщенного пара при данной температуре. (Или парциального давления водяного пара в атмосфере к давлению насыщенного пара при данной температуре).

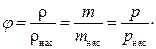
Точка росы — температура, при которой пар становится насыщенным, т. е. когда относительная влажность равна 100 %.

2.7. Электростатика

Электростатика изучает взаимодействие неподвижных заряженных тел.

Электрический заряд q (Кл) — количественная мера электромагнитного взаимодействия между телами.

В дальнейшем под электрическим зарядом (зарядом) будем подразумевать заряженное тело.

Точечный заряд – это заряженная материальная точка.

Заряды бывают двух видов: положительные и отрицательные. Одноименные заряды отталкиваются, а разноименные заряды — притягиваются.

Дискретность заряда: любой заряд состоит из целого числа элементарных зарядов:

q = N e,

где e = ± 1,6×10^-19 Кл - элементарный заряд.

Элементарный электрический заряд — заряд, которым обладают элементарные частицы — электрон и протон. Положительным элементарным зарядом обладает протон, отрицательным — электрон.

Закон сохранения заряда:

В электроизолированной системе алгебраическая сумма зарядов постоянна.

Q = q ₁ + q ₂+¼+ q _n = const.

Закон Кулона:

Два точечных заряда взаимодействуют с силой, прямо пропорциональной произведению их модулей и обратно пропорциональной квадрату расстояния между ними. Сила Кулона направлена вдоль линии, соединяющей эти заряды.

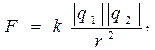
где k = 1/(4pe₀) = 9 10⁹ (Н×м² / Кл²) ¾ коэффициент пропорциональности;

e₀ = 8,85×10^-12 Ф/м - электрическая постоянная.

Заряженную сферу или заряженный шар можно заменить таким же по значению точечным зарядом, находящимся в центре.

Направление кулоновской силы определяется знаками взаимодействующих зарядов.

Электрическое поле — материальная субстанция, через которую осуществляется взаимодействие электрических зарядов.

Электростатическое поле — поле, создаваемое неподвижными зарядами.

Напряженность 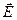(В/м), (Н/Кл) электрического поля — векторная величина, равная отношению силы 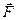, с которой электрическое поле действует на положительный точечный заряд q ₀ (пробный заряд), помещенный в данную точку поля, к величине этого заряда:

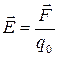
Вектор напряженности электрического поля совпадает по направлению с кулоновской силой, действующей на положительный заряд, помещенный в данную точку электрического поля.

Электрическое поле точечного заряда.

Напряженность Е электрического поля, создаваемого точечным зарядом q в вакууме на расстоянии r от заряда:

,

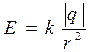q > 0 — вектор напряженности направлен от заряда.

q < 0 — вектор напряженности направлен к заряду.

Силовая линия — линия, касательные к которой в каждой точке совпадают с вектором напряженности электрического поля.

Силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных.

Однородным называется электрическое поле, в котором вектор напряженности одинаков во всех точках. Силовые линии однородного поля — параллельные прямые.

Принцип суперпозиции полей (для напряженности):напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов.

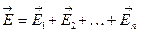
Потенциал ¾ энергетическая характеристика электрического поля. Потенциал численно равен отношению потенциальной энергии W_p пробного заряда, помещенного в данную точку электрического поля, к величине этого заряда q ₀.

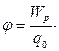
Потенциал численно равен работе, совершаемой полем, при перемещении заряда + 1 Кл из данной точки поля в бесконечность. Потенциал бесконечно удаленной точки поля считается равным нулю.

Потенциал поля точечного заряда определяется по формуле:

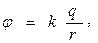
где r - расстояние от заряда до точки электрического поля.

Принцип суперпозиции (для потенциала): потенциал поля системы зарядов равен алгебраической сумме потенциалов полей каждого из зарядов в данной точке.

j = j₁ + j₂ +... + j_n

Работа электростатического поля по перемещению заряда равна произведению величины перемещаемого заряда q на разность потенциалов в начальном j₁ и конечном j₂положениях заряда:

A = q (j₁ – j₂).

Следствие: работа электростатического поля по замкнутой траектории равна нулю, так как в этом случае

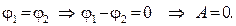
Работу электростатического поля также вычисляется по формуле:

A = qE D r cosa,

где D r — перемещение заряда; a — угол между направлением вектора напряженности электрического поля и направлением перемещения заряда.

Диэлектрики — вещества, в которых нет свободных зарядов. Поэтому диэлектрики не проводят электрический ток.

Если диэлектрик поместить во внешнее электрическое поле, то напряженность поля внутри диэлектрика будет меньше, чем в вакууме.

Диэлектрическая проницаемость среды e показывает, во сколько раз напряженность поля в вакууме Е ₀ больше напряженности поля в данной среде Е:

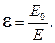
В диэлектрике кулоновская сила, напряженность и потенциал поля уменьшаются в e раз:

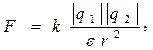
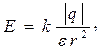
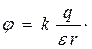
Проводники — вещества, имеющие свободные электрические заряды и способные проводить электрический ток.

Напряженность электрического поля в проводнике равна нулю Е = 0, а потенциал поля постоянен j = const.

Электрическая емкость С (Ф)равна отношению заряда проводника q к потенциалу проводника j:

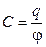
Электроемкость зависит от геометрической формы и размеров проводника и от диэлектрической проницаемости среды, в которой находится проводник.

Конденсатор состоит из двух проводников — обкладок, заряженных разноименными и равными по абсолютной величине зарядами.

Емкость конденсатора

,

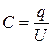где q — заряд на обкладке, U = j₁ - j₂ — напряжение на обкладках конденсатора.

Плоский конденсатор состоит из двух плоских параллельных пластин, между которыми находится диэлектрик.

Емкость плоского конденсатора определяется по формуле:

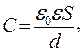
где d - расстояние между пластинами, S - площадь пластины, e₀ - электрическая постоянная, e - диэлектрическая проницаемость среды в конденсаторе.

Емкость сферического конденсатора определяется по формуле:

C = 4pee₀ R,

где R — радиус конденсатора.

Энергия W электрического поля конденсатора:

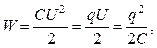
где С - емкость конденсатора, U – напряжение (разность потенциалов) между пластинами, q - заряд на пластине.

Соединения конденсаторов (рис. 12, рис. 13):

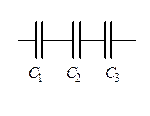
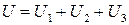
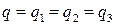
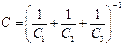
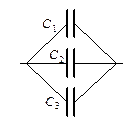
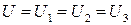
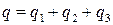
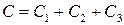
Рис. 12 Последовательное соединение		Рис. 13 Параллельное соединение

Дата добавления: 2015-10-23