Теоретическое введение. Лабораторная работа № 41

Лабораторная работа № 41

Определение фокусных расстояний линз методом Бесселя

1. Цель работы: определение фокусного расстояния линзы методом Бесселя.

2. Вид занятия: лабораторное занятие.

3. Продолжительность: 3 академических часа (135 мин.)

4. Оборудование: лазер, дифракционная решетка, система линз, экран, оптическая скамья, измерительная лента.

5. Содержание занятия: теоретическое введение; описание установки; контроль исходного уровня знаний; самостоятельная работа студентов; контроль степени усвоения материала по тестам; подведение итогов занятия.

Теоретическое введение

Линзой называется прозрачное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями, преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т.д. Обычно применяют линзы, поверхности которых имеют сферическую форму. Основные типы линз изображены на рис.1. Различают тонкие и толстые линзы. Линза называется тонкой, если её толщиной можно пренебречь по сравнению с радиусами кривизны её поверхностей.

Система, состоящая из одной или нескольких линз, называется центрированной, если центры кривизны всех её преломляющих поверхностей лежат на одной прямой, называемой оптической осью.

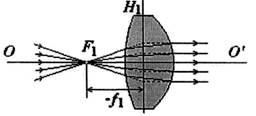
Рис.2. Прохождение пучка лучей, сходящихся в первом главном фокусе F1, через двояковыпуклую линзу
Рис. 1. Основные типы линз: собирающие: 1 - двояковыпуклая; 2 - плосковыпуклая; 3 - вогнуто-выпуклая (положительный мениск), рассеивающие; 4 - двояковогнутая; 5 - плосковогнутая, 6 - выпукло-вогнутая (отрицательный мениск)
Рис.2'. Прохождение пучка лучей параллельного оптической оси через двояковыпуклую линзу

Вспомним основные свойства центрированной системы на примере толстой двояковыпуклой стеклянной линзы, находящейся в воздухе.

Лучи, проходящие через первый главный фокус F₁, выходят с другой стороны линзы пучком, параллельным главной оптической оси ОО′ (рис. 2). Главный фокус находится на расстоянии -f₁ от первой главной плоскости H₁, которая определяется как геометрическое место точек пересечения падающих лучей с их продолжениями за линзой. Здесь и далее всем расстояниям, отсчитываемым против хода лучей, приписывается знак "-" (правило знаков).

Пучок лучей, падающих на линзу параллельно главной оптической оси, сходится во втором главном фокусе F₂, отстоящем на расстоянии f₂ от второй главной плоскости Н₂ (рис.2').

Если по обе стороны от линзы находится одна и та же среда, фокусные расстояния совпадают: -f₁ = f₂ = f. Величина D = 1/f называется оптической силой линзы.

Собирающая линза сводит лучи, параллельные оптической оси в действительном фокусе (f>0, рис.3), и имеет положительную оптическую силу.

Оптическая сила рассеивающей линзы отрицательна, так как для неё точка схождения параллельных лучей мнимая (f<0, рис. 4).

Для тонкой линзы можно считать, что точки пересечения поверхностей с оптической осью сливаются в одну точку, называемую оптическим центром, а главные плоскости H₁, Н₂ - в одну плоскость, проходящую через оптический центр линзы перпендикулярно её главной оптической оси.

Если светящийся предмет – это небольшой отрезок, перпендикулярный к оптической оси, то его изображение, полученное с помощью параксиальных (приосевых) лучей также имеет вид отрезка, перпендикулярного к оптической оси (рис. 5). Расстояния до предмета и до его изображения s и s′, отсчитанные от оптического центра вдоль главной оптической оси и взятые с учётом правила знаков, подчиняются уравнению линзы (1). Для тонкой собирающей линзы f можно рассчитать по этой формуле, получив действительное изображение предмета и измерив расстояния s и s'.

Рис. 3. Собирающая линза сводит пучок лучей, параллельных OO′ в действительном фокусе	Рис. 5. Построение изображения в тонкой положительной линзе	Рис. 6. Построение изображения в толстой положительной линзе
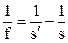	; (1) f-фокусное расстояние линзы s′-расстояние до изображения s-расстояние до предмета
Рис. 4. Такой же пучок после преломления в рассеивающей линзе кажется исходящим из мнимого фокуса	Рис. 7. Положение главных плоскостей для различных линз

Формула (1) справедлива и для толстой линзы. Однако воспользоваться ею для определения фокусного расстояния произвольной линзы затруднительно, поскольку все расстояния в случае толстых линз или оптических систем необходимо отсчитывать от соответствующих главных плоскостей (рис. 6). Главные плоскости могут лежать и внутри, и вне линзы, совершенно несимметрично относительно её сферических поверхностей (рис. 7), и их положение, как правило, неизвестно.

В таблице приведены особенности изображений в линзах. Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно - перевернутое), положительным – мнимое изображение (оно - прямое).

Линза	Расположение предмета	Расположение изображения	Особенности изображения
Собирающая	За двойным фокусным расстоянием	Между фокусом и двойным фокусом по другую сторону линзы	Действительное, перевернутое, уменьшенное
В двойном фокусе	В двойном фокусе по другую сторону линзы	Действительное, перевернутое, по величине равно самому предмету
Между двойным фокусным расстоянием и фокусом	За двойным фокусным расстоянием по другую сторону линзы	Действительное, перевернутое, увеличенное
В фокусе	Видимого изображения нет (изображение в бесконечности)
Между фокусом и линзой	За предметом, по ту же сторону линзы, что и предмет	Мнимое, прямое, увеличенное
Рассеивающая	Любое	Между предметом и линзой, по ту же сторону линзы, что и предмет	Мнимое, прямое, уменьшенное

Комбинация собирающих и рассеивающих линз применяется в оптических приборах, используемых в том числе и в медицине. Так, широкое применение в медицине имеет оптический микроскоп. В современных оптических микроскопах объектив и окуляр состоят из системы линз, представляющей собой оптическую систему. Качество оптических изображений реальных оптических систем может снижаться из-за возникновения погрешностей, или так называемых аберраций. Основными аберрациями линз являются:

а) сферическая аберрация;

б) хроматическая аберрация;

в) астигматизм;

г) дисторсия.

Сферическая аберрация заключается в том, что края линзы вследствие большей кривизны поверхности преломляют сильнее, чем центральная часть Изображение светящейся точки на экране имеет вид светлого пятна.

Для устранения сферической аберрации создают систему из вогнутой и выпуклой линз.

Хроматическая аберрация наблюдается в связи с тем, что вследствие дисперсии лучи с различной длиной волны (например, красные и фиолетовые) преломляются в линзе неодинаково, и фокусы для них не совпадают. Вследствие этого линия контуров в изображении предметов имеют вид узких спектральных окрашенных полосок.

Хроматическая аберрация устраняется в системе из двух линз, изготовленных из стекла различного цвета с соответственно подобранной дисперсией. Подобная система линз (в котором скомпенсирована также и сферическая аберрация), называется ахроматом.

Если оно достаточно велико, существуют два положения линзы, при которых на экране получаются чёткие изображения предмета - уменьшенное и увеличенное (рис. 2).

Астигматизм – это недостаток оптической системы, при которой сферическая световая волна, проходя оптическую систему, деформируется и перестает быть сферической

Различают два вида астигматизма. Один из них обусловлен падением на оптическую систему лучей, составляющих значительный угол с оптической осью (астигматизм косых пучков).

Другой вид астигматизма обусловлен асимметрией оптической системы. Линзы с такой аберрацией называют астигматическими. Эти линзы, аналогично астигматизму косых пучков, создают изображение, в котором контуры и линии, ориентированные в разных направлениях, имеют разную резкость.

Для исправления астигматизма создают сложные оптические системы, состоящие из нескольких линз, благодаря чему удается образовать хорошие изображения при углах падения лучей 50^о-70^о или применяют линзы, ограниченные цилиндрическими поверхностями. Система линз (объективов), исправленная по рассмотренным аберрациям, называется анастигматом.

Дисторсия обусловлена тем, что линейное увеличение линзы для точек предмета, находящихся на различных расстояниях от главной оси, несколько различается. В связи с этим прямые контуры предмета, лежащие в плоскости, перпендикулярной главной оси, принимают дугообразную форму. Дисторсия устраняется путем подбора системы линз с противоположным характером дисторсии.

Удобным методом определения фокусного расстояния является используемый в данной работе метод Бесселя, который позволяет найти величину f, не зная положение главных плоскостей линзы.

Дата добавления: 2015-10-29