A short theory

A hydrogen atom has one electron which "rotates" in a nuclear field. An electric force on Coulomb attraction acts between the electron and the nucleus. The potential energy of an electron in a nuclear field is

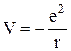, (11.1)

where e is the charge of an electron and r is the distance between the nucleus and electron. Such an atom constitutes a peculiar kind of potential well and is illustrated in fig.11.1.

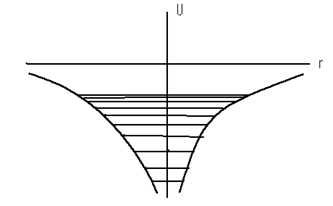
Figure 11.1

The electron inside the atom has a negative potential energy since the minimum value of potential energy tends to infinity when r → 0 and the maximum value is equal to zero. Fig. 11.2 shows the energy levels obtained from the solution of the Schrodinger equation

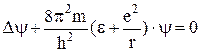. (11.2)

Figure 11.2

An important feature of the solution is the drawing together of the levels as the quantum number n increases. The scales of values, which are proportional to energy are given in the units adopted in spectroscopy: volts and reciprocal centimetres. The energy level formula may by written in the form

. (11.3)

For historical reasons, it is customary to write this formula in the for

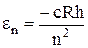, (11.4)

where

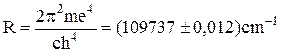(11.5)

is the Rydberg’s constant.

The atomic electron may be located at any one of n levels. The energy of a free hydrogen atom on which no force acts is at the lowest energy level

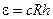, (11.6)

The energy ε = cRh is called the ionisation energy. If the energy imparted to hydrogen atom is less than cRh, a transition of the atom occurs to one of the n levels. Such an atom is said to be in an exited state.

An atom stays in an excited state for a small fraction of a second and then passes to a lower level with the emission off a photon in accordance with the equation

hν_mn = ε_m - ε_n = cRh (1/n² - 1/m²). (11.7)

By calculating for a given n the ν frequencies corresponding to the numbers m = n +1, n +2,..., we obtain a series of frequencies of lines in the hydrogen spectrum. The series corresponding to n = 2 is known as the Balmer series.

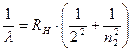. (11.8)

Дата добавления: 2015-10-29