Kristallarning issiqlik sig’mi

Kristall panjaraning ichki energiyasi uni tashkil qilgan atom va molekulalar energiyalarining yiindisidan iborat. Madomiki, kristall atomlari tebranma harakatda bo’lib, fononlar hosil qilib turar ekan, u holda kristallning to’la energiyasi undagi fononlar energiyasining yiindisiga teng.

Kristall panjarasining issiqlik siimi uning xaroratini 1 gradusga orttirish uchun kerak bo’lgan issiqlik miqdorini bildiradi

Jismga yoki ular sistemasiga issiqlik berilsa, termodinamikaning 1 - qonuniga ko’ra dQ=dU+rdV=dU, chunki kristallning xajmi sezilarli o’zgarmaydi. U xolda

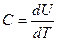, (14.4)

bu yerda dU - kristall ichki energiyasining o’zgarishi.Buni eotiborga olsak, kristallning issiqlik siimi uning xarorati 1 gradusga ortganda kristallning ichki energiyasi qanchaga o’zgarishini bildiradi.

Demak, kristall issiqlik siimini aniqlash uchun uning ichki energiyasining xaroratga bolanishini bilish kerak. Kristall kvant sistema bo’lgani uchun uning ichki energiyasini kvant statistikasi yordamida aniqlaymiz.

dU= wdN (14.5)

bu yerda dN chastotalari w va w+dw oraliida bo’lgan kristalldagi fononlarning soni

dN=n ^. f ^. dg (13.6)

bundagi n=3, chunki bir xil chastotali 3 xil fononlar bir yo’nalishda tarqalishi: (ikkita ko’ndalang va bitta bo’ylama fononlar mavjud bo’lishi) mumkin; - ipulpslari r va r+dr intervalda bo’lgan kvant holatlar zichligi; Boze - Eynshteyn taqsimot funksiyasi, chunki fononlarning spini butun son yoki 0 ga teng va ular uchun m=0.

Endi fononning energiya va impulpslari bilan chastotasi orasidagi maolum bolanishlarni ye= w va r= w/v (v - fononning tezligi) inobatga olib, (14.6) ni quyidagicha yozamiz

(14.7)

U holda kristalldagi chastotalari w va w+dw bo’lgan fononlarning energiyasi

.

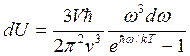Bundan

, (13.8)

bu yerda w_m = - fononlarning maksimal chastotasi.

(14.8) dan T bo’yicha xosila olib, kristall panjara issiqlik siimining umumiy ifodasini topish mumkin. Soddalik uchun past va yuqori temperaturalardagi issiqlik siimini aniqlaymiz:

1-xol. Yuqori temperaturlar so’asida w<<kT bo’lgani uchun

deb olish mumkin.

U xolda

yaoni

U=U₀ + 3kTN (14.9)

bu yerda U₀ – kristall panjaraning T = 0 dagi ichki energiyasi.

Bir molp kristallda N=N_A bo’lgani uchun U_m = 3N_A kT.

U xolda yuqori temperaturalarda kristallning molyar issiqlik siimi

S=dU/dT=3kN_A=3R (14.13)

(14.13) xaqiqatdan xam Dyulong va Ptilar tajribada aniqlagan natijaning aynan o’zidir.

2 -xol. Past temperaturalar so’asi w>>kT.

(14.8) da o’zgaruvchilarni quyidagicha almashtiramiz:

x= w/kT, x_m= w_m/kT va w_m=kq (14.13)

bu yerda q ni - Debayning xarakteristik xarorati deyiladi. Uning maonosi quyidagicha: xarorat 0 dan q gacha o’zgarganda kristallda chastotalari 0 dan w_m gacha mumkin bo’lgan fononlar hosil bo’ladi. q dan boshlab kristallda w_m dan katta chastotali fononlar hosil bo’lmaydi.

(14.13) dan

(14.13)

(14.13) ni (13.8) ga qo’yamiz

bundagi

ekanini inobatga olsak,

yoki

U xolda issiqlik siimi

yoki

Demak, past temperaturalarda issiqlik siimi temperaturaning kubiga proporsional ekan

S~T³

Buning sababi shuki, xaroratning ortishi bilan fononlarning konsentrasiyasi T³ bo’yicha ortadi.

Xaroratning oraliq so’asida ichki energiya va issiqlik siimi murakkabroq o’zgaradi. Umumiy holda (14.8) dan T bo’yicha hosila olib S ni topish mumkin. harorat q ga yaqinlashgani sari fononlar konsentrasiyasining ortishi ham sekinlashadi.

Дата добавления: 2015-10-29