Применение линейного программирования

Оптимизация раскроя листа древесно-стружечной плиты (ДСП)

В качестве раскраиваемого материала в данном случае будет выступать лист древесно-стружечной плиты (ДСП) размером 2770х2440мм. Пусть заготовка имеет длину L = 2770мм, и ширину 1 = 2440мм. При разрезке листа на заготовки одного размера возможны значительные отходы из-за некратности L по отношению к 1. Для сокращения отходов в условиях многономенклатурного производства применим групповой раскрой, при котором лист разрезают на заготовки различной длины из заданной номенклатуры. В нашем случае разделение материала происходит в направлении двух размеров листа и считается двумерным.

Применение линейного программирования

Оптимизация раскроя двумерного материала сводится к решению задачи линейного программирования (ЛП). Теоретическая задача по раскрою материала была рассмотрена в разделах 3.1 - 3.5, поэтому приступим к решению практической задачи, поставленной на предприятии. Исходные данные: значения L и / известны, а также требуемое число (партии) [N] столов.

Рассмотрим конкретный пример раскроя листов на комплектующие: крышка (S]= 1100х680мм²⁾, ножка (S₂= 710х560мм²⁾, панель задняя (S3—970х80мм). Требуемое число заготовок соответственно: [N] = 100, 200, 100 шт. Пропил материала составляет 4мм. Оценочная функция — число листов, расходуемое на выполнение всего заказа.

Рисунок 13 - План раскроя №1

Разместим заготовки таким образом, что их число, расположенное на листе будет рациональным (S_отхода=4998мм²). При размещении заготовок следует учитывать ширину пропила. Чем большее количество заготовок будет размещено на листе, тем больше будет ширина пропила. Из первого плана получаем, что: крышек - 6 штук, ножек - 3 штуки, панелей задних - 8 штук.

Рисунок 14 - План раскроя №2

При втором варианте расположения заготовок (S_отхода=4220мм). Количество крышек - 2 штук, ножек - 12 штуки, панелей задних - 2 штук.

Рисунок 15 - План раскроя №3

В третьем варианте расположения заготовок (S_отхода=5165мм²). Количество крышек - 4 штук, ножек - 8 штуки, панелей задних - 3 штук. Дальнейшие варианты расположения комплектующих стола нас не устраивают, т.к. они не соответствуют рациональному расходу материала. План №4: крышек 2 шт., ножек 10 шт., панелей задних 4 шт. (S_отхода^:=9816мм²). План №5: крышек - 3 шт., ножек - 9 шт., панелей задних -1 шт. (S_отхода =l 1428мм²). Ниже приведена таблица 18.

Таблица 18 - Варианты раскроя листа ДСП заданного размера

Найдем значения переменных, обеспечивающих минимум оценочной функции:

Т.е. из общего числа израсходованных листов. Система уравнений ограничений учитывает требуемые количества заготовок N:

Коэффициентами при неизвестных являются числа заготовок в соответствующих столбцах таблицы. Уравнения (25), (26) линейны, в зависимости от общего числа переменных п они описывают прямые (п = 2), плоскости (n = 3) или гиперплоскости (n > 3). Система ограничений (2) определяет границы так называемой области допустимых решений (ОДР): многоугольника, многогранника или гипермногогранника в n-мерном пространстве. Минимум оценочной функции можно найти простым перебором вариантов решения, поочередно подставляя координаты вершин ОДР, т.е. соответствующие значения переменных в уравнение оценочной

функции. Существуют методы, ускоряющие решение задачи. Применим один из них - - симплекс-метод Дж. Данцига, используя преобразование таблиц с разрешающим элементом. Преобразование начинают с табл. 18, приведенной ниже, которая содержит уравнения (26), записанные в виде:

Уравнения (27) представлены в таблицу 18.

Таблица 18 - Матричное преобразование линейных уравнений

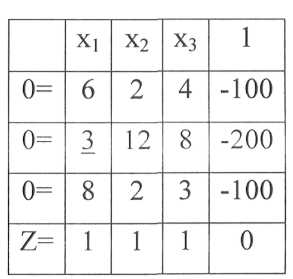
Подчеркнутый элемент выбран в качестве разрешающего, его роль сформулирована в п. 3.1.На втором этапе разрешающий столбец остается без изменений, числа разрешающей строки, кроме разрешающего элемента, записывают в новую таблицу с обратными знаками. Остальные элементы таблицы (разумеется, кроме левого столбца и верхней строки, где располагаются переменные) пересчитывают по правилу прямоугольника и затем переносят в новую таблицу. Правило проиллюстрировано в п. 3.1 (см. табл. 6).

На следующем этапе алгоритма элементы заполняемой таблицы делятся на разрешающий элемент, а сам он заменяется обратной величиной и

в таком виде входит в новую таблицу В итоге новые значения чисел преобразуемой таблицы оказываются следующими:

Изложенные правила относятся к общему случаю преобразования таблиц, когда их размерность остается неизменной. В случае замены 0-строки на 0-столбец последний не подлежит переносу в новую таблицу, а попросту аннулируется. Также оказывается излишним третий этап алгоритма, если разрешающий элемент таблицы равен единице. После преобразования таблица 18 приобретает иной вид (табл. 19).

Таблица 19 - Преобразование таблицы 18

Пересчитываем таблицу 19. Выбираем разрешающий элемент, в данном случае им будет -22 (подчеркнут в таблице 19). С учетом разрешающего элемента необходимо избавиться от отрицательных значений в строке Z, число -3.

Таблица 20 -Преобразование таблицы 19

В получившейся таблице 20, нас интересуют следующие значения. Во-первых, в строке Z нет отрицательных чисел - это говорит о том, что первый этап мы пересчитали без ошибок и достигли поставленной цели (избавиться от отрицательных значений строки Z). Во-вторых, для самопроверки необходимо проверить, соблюдение первоначального условия поставленной задачи, а именно: Z=x₁+x₂+x₃. Итак, делаем проверку:

Тождество 29 выполняется, значит, решение верное. Однако, дробных значений, очевидно, быть не может (1,5 крышки или 1,2 ножки). Поэтому для избавления от дробных значений необходимо увеличить минимальную изначальную партию со 100 до 3300 столов.

Получаем,

x₁ =400,х₂ =450

Крышки: 6 * 400 + 2 * 450 = 3300 (шт.), Ножки: 3 * 400 + 12 * 450 = 6600(шт.)_;

Панели: 8 * 400 + 2 * 450 = 4100(шт.),

Имеем, задел панелей 4100 — 3300 = 800 (шт.).

Задел панелей в 800 штук, говорит нам о том, что в следующей партии необходимо будет сделать поправку. В таком случае получаем для второй партии:

Крышки: 6 * 400 + 2 * 450 = 3300 (шт.), Ножки: 3 * 400 + 12 * 450 = 6600(шт.), Панели: 4 * 400 + 2 * 450 = 2500(шт.). Необходимо будет уменьшить количество раскроя панелей в 2 раза.

Операции раскроя листов по выбранным планам

Для раскроя листа, на который был намечен план распила заготовок, оператору распиловочного станка необходимо знать, с какой операции начать выполнять распиливание, чтобы рационально отделить из заданного материала необходимые для сборки заготовки, при этом, не испортив, сам материал.

Использование в мебельном производстве различных типов древесно­стружечных плит вынуждает фирмы, занимающиеся изготовлением мебели, обзаводиться специальным оборудованием для распила (или раскройки) листов ДСП. Таким оборудованием является распиловочный станок для ДСП.

Основными составными частями распиловочного станка являются:

- поперечный (горизонтальный) стол для установки плиты;

- шариковая или роликовая каретка для перемещения плиты вдоль
пильного механизма;

- пильный механизм, состоящий из одного или двух режущих узлов;

- режущий узел, оснащенный основной и подрезной пилами.

Каждая деталь распиловочного станка имеет строго определенное предназначение. Пильный узел практически у всех модификаций станков имеет возможность изменения угла наклона до 45 градусов, что повышает качество резки. Основная пила глубоко раскраивает лист ДСП, а подрезная -точным движением дорезает нижний край, защищая от повреждений и сколов ламинированную или шпонированную поверхность плиты.

Рисунок 16 — Операции плана раскроя № 1

Обозначим операции для раскроя листа по плану № 1.

1) Отделение кромки листа. Первичная операция, которая необходима для определения границ распиливания на заготовки.

Рисунок 17 - Операции раскроя

2) Отделение ножек (Зшт.)

Рисунок 18 - Операции раскроя

3) Отделение крышек (6шт.)

Рисунок 19- Операции раскроя

4) Отделение оставшейся части отхода от панелей

Рисунок 20 — Операции раскроя

5) Распиливание на единичные образцы, массивных заготовок: крышек - 6шт., ножек - Зшт., панелей - 8шт.

Рисунок 21 - Операции плана раскроя №2

Обозначим операции для раскроя листа по плану №2.

1) Отделение кромки листа

Рисунок 22 — Операции раскроя

2) Отделение ножек от основной площади листа, с последующей операцией отделения части отхода от основной площади ножек.

Рисунок 23 - Операции раскроя

3) Отделение панелей, с последующим отделением части отхода

Рисунок 24 - Операции раскроя

4) Отделение части крышек

Рисунок 25 - Операции раскроя

5) Отделение оставшейся части отхода от ножек

Рисунок 26 - Операции раскроя

6) Распиливание на единичные образцы, массивных заготовок: крышек - 2шт., ножек - 12шт., панелей - 2шт.

В данном разделе была решена задача по оптимизации раскроя листа ДСП заданных размеров. Проведены расчеты с применением симплекс метода Дж. Данцига. В ходе расчетов выяснилось, что третий избранный план раскроя можно не применять в производственном процессе. Описаны операции по раскрою массивного листа на заготовки указанных размеров.

Дата добавления: 2015-10-29